Giải vth Toán 9, soạn vở thực hành Toán 9 KNTT

Bài 18. Hàm số y = ax² (a ≠ 0) trang 5, 6, 7 Vở thực hà..

Giải câu hỏi trắc nghiệm trang 5, 6 vở thực hành Toán 9 tập 2

Điểm nào sau đây thuộc đồ thị hàm số (y = frac{1}{3}{x^2})? A. (left( {3;1} right)). B. (left( { - 3;1} right)). C. (left( {3; - 3} right)). D. (left( { - 3;3} right)).

Tổng hợp đề thi học kì 1 lớp 9 tất cả các môn - Kết nối tri thức

Toán - Văn - Anh - KHTN - Lịch sử và Địa lí

Lựa chọn câu để xem lời giải nhanh hơn

Chọn phương án đúng trong mỗi câu sau:

Câu 1

Trả lời Câu 1 trang 5 Vở thực hành Toán 9

Điểm nào sau đây thuộc đồ thị hàm số \(y = \frac{1}{3}{x^2}\)?

A. \(\left( {3;1} \right)\).

B. \(\left( { - 3;1} \right)\).

C. \(\left( {3; - 3} \right)\).

D. \(\left( { - 3;3} \right)\).

Phương pháp giải:

Thay hoành độ của các điểm vào hàm số \(y = \frac{1}{3}{x^2}\) để tìm tung độ. Từ đó tìm được điểm thuộc đồ thị.

Lời giải chi tiết:

Thay \(x = 3\) vào hàm số \(y = \frac{1}{3}{x^2}\) ta có: \(y = \frac{1}{3}{.3^2} = 3\). Do đó, điểm (3; 3) thuộc đồ thị hàm số \(y = \frac{1}{3}{x^2}\).

Thay \(x = - 3\) vào hàm số \(y = \frac{1}{3}{x^2}\) ta có: \(y = \frac{1}{3}.{\left( { - 3} \right)^2} = 3\). Do đó, điểm (-3; 3) thuộc đồ thị hàm số \(y = \frac{1}{3}{x^2}\).

Chọn D

Câu 2

Trả lời Câu 2 trang 5 Vở thực hành Toán 9

Điểm A(-2; -2) thuộc đồ thị hàm số \(y = a{x^2}\) khi

A. \(a = - 1\).

B. \(a = 1\).

C. \(a = - \frac{1}{2}\).

D. \(a = \frac{1}{2}\).

Phương pháp giải:

Thay \(x = - 2;y = - 2\) vào hàm số \(y = a{x^2}\), giải phương trình tìm được a.

Lời giải chi tiết:

Thay \(x = - 2;y = - 2\) vào hàm số \(y = a{x^2}\) ta có: \( - 2 = a.{\left( { - 2} \right)^2}\), suy ra \(a = \frac{{ - 1}}{2}\). Do đó, \(a = \frac{{ - 1}}{2}\) thì điểm A(-2; -2) thuộc đồ thị hàm số \(y = a{x^2}\).

Chọn C

Câu 3

Trả lời Câu 3 trang 5 Vở thực hành Toán 9

Cặp điểm nằm trên đồ thị \(y = 2{x^2}\) có tung độ bằng 4 là

A. \(\left( {2;4} \right)\) và \(\left( { - 2;4} \right)\).

B. \(\left( {4;2} \right)\) và \(\left( {4; - 2} \right)\).

C. \(\left( {\sqrt 2 ;4} \right)\) và \(\left( { - \sqrt 2 ;4} \right)\).

D. \(\left( {4;\sqrt 2 } \right)\) và \(\left( {4; - \sqrt 2 } \right)\).

Phương pháp giải:

Thay \(y = 4\) vào hàm số \(y = 2{x^2}\) để tìm x, từ đó tìm được tọa độ điểm thuộc đồ thị hàm số.

Lời giải chi tiết:

Thay \(y = 4\) vào hàm số \(y = 2{x^2}\) ta có: \(4 = 2.{x^2}\), suy ra \({x^2} = 2\) nên \(x = \pm \sqrt 2 \).

Vậy các cặp điểm \(\left( {\sqrt 2 ;4} \right)\) và \(\left( { - \sqrt 2 ;4} \right)\) nằm trên đồ thị \(y = 2{x^2}\) có tung độ bằng 4.

Chọn C

Câu 4

Trả lời Câu 4 trang 6 Vở thực hành Toán 9

Hình bên là đồ thị của hàm số nào?

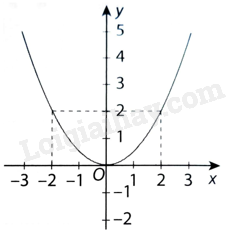
A. \(y = \frac{1}{4}{x^2}\).

B. \(y = \frac{1}{2}{x^2}\).

C. \(y = {x^2}\).

D. \(y = 2{x^2}\).

Phương pháp giải:

Dựa vào đồ thị ta thấy những điểm (0; 0), (2; 2); (-2; 2) đều thuộc đồ thị hàm số \(y = \frac{1}{2}{x^2}\).

Lời giải chi tiết:

Đồ thị hàm số trên đi qua các điểm (0; 0), (2; 2); (-2; 2). Do đó, đồ thị hàm số cần tìm là \(y = \frac{1}{2}{x^2}\).

Chọn B

Câu 5

Trả lời Câu 5 trang 6 Vở thực hành Toán 9

Điểm M(-2; -3) nằm trên đồ thị của hàm số nào dưới đây?

A. \(y = - \frac{3}{4}{x^2}\).

B. \(y = - \frac{3}{2}{x^2}\).

C. \(y = \frac{3}{4}{x^2}\).

D. \(y = \frac{3}{2}{x^2}\).

Phương pháp giải:

Thay \(x = - 2\) vào hàm số \(y = - \frac{3}{4}{x^2}\), tìm được tung độ nên tìm được điểm nằm trên đồ thị hàm số \(y = - \frac{3}{4}{x^2}\).

Lời giải chi tiết:

Thay \(x = - 2\) và hàm số \(y = - \frac{3}{4}{x^2}\) ta có: \(y = - \frac{3}{4}.{\left( { - 2} \right)^2} = - 3\). Do đó, điểm M(-2; -3) nằm trên đồ thị của hàm số \(y = - \frac{3}{4}{x^2}\)

Chọn A

Bình luận

Chia sẻ

Bình chọn:

4.9 trên 7 phiếu

Bài tiếp theo

Giải bài 1 trang 6 vở thực hành Toán 9 tập 2
Cho hàm số (y = 0,25{x^2}). Hoàn thành bảng giá trị sau vào vở:
Giải bài 2 trang 6 vở thực hành Toán 9 tập 2
Cho hình lăng trụ đứng có đáy là hình vuông cạnh a (cm) và chiều cao 10cm. a) Viết công thức tính thể tích V của lăng trụ theo a và tính giá trị của V khi (a = 2cm). b) Nếu độ dài cạnh đáy tăng lên hai lần thì thể tích của hình lăng trụ thay đổi thế nào?
Giải bài 3 trang 6 vở thực hành Toán 9 tập 2
Diện tích toàn phần (Sleft( {c{m^2}} right)) của hình lập phương, tức là tổng diện tích xung quanh và diện tích đáy hai mặt của hai mặt đáy là một hàm số của độ dài cạnh a (cm). a) Viết công thức của hàm số này. b) Sử dụng công thức nhận được ở câu a để tính độ dài cạnh của một hình lập phương có diện tích toàn phần là (54c{m^2}).
Giải bài 4 trang 7 vở thực hành Toán 9 tập 2
Vẽ đồ thị của các hàm số sau: a) (y = 3{x^2}); b) (y = - frac{1}{3}{x^2}).
Giải bài 5 trang 8 vở thực hành Toán 9 tập 2
Biết đường cong trong hình bên là một parabol (y = a{x^2}). a) Tìm hệ số a. b) Tìm tung độ của điểm thuộc parabol có hoành độ (x = - 2). c) Tìm các điểm thuộc parabol có tung độ (y = 8).
Giải bài 6 trang 8 vở thực hành Toán 9 tập 2
Trong hình sau có hai đường cong là đồ thị của hai hàm số (y = - 3{x^2}) và (y = {x^2}). Hãy cho biết đường nào là đồ thị của hàm số (y = - 3{x^2}).
Giải bài 7 trang 8 vở thực hành Toán 9 tập 2
Cho parabol (y = {x^2}) và đường thẳng d có phương trình (y = - 2x + 3). a) Vẽ parabol và đường thẳng trên cùng một hệ trục tọa độ Oxy. b) Từ đồ thị suy ra tọa độ các giao điểm A và B của đường thẳng và parabol.
Giải bài 8 trang 9 vở thực hành Toán 9 tập 2
Một cổng vòm được thiết kế dạng parabol (y = a{x^2}) như hình dưới đây. Biết chiều rộng của chân cổng là (AB = 6m) và chiều cao cổng là (OI = 4,5m). a) Tìm hệ số a dựa vào các dữ kiện trên. Từ đó, tính độ dài đoạn HK biết H cách điểm chính giữa cổng I là 2m. b) Để vận chuyển hàng qua cổng, người ta dự định sử dụng một xe tải có chiều rộng 2m, chiều cao 3m. Hỏi xe tải này có thể đi qua được cổng vòm đó hay không?
Giải bài 9 trang 9 vở thực hành Toán 9 tập 2
Khi bỏ qua sức cản của không khí, một vật rơi tự do sau t giây thì rơi được quãng đường (s = 4,9{t^2};left( m right)). Bạn Minh thả một hòn đá rơi từ miệng giếng xuống một cái giếng cạn sâu 100m. a) Hỏi sau 1 giây, 2 giây, 3 giây, 4 giây thì hòn đá lần lượt cách đáy giếng bao nhiêu mét? b) Thời gian từ lúc hòn đá bắt đầu rơi đến lúc chạm đáy giếng là bao lâu (làm tròn đến hàng phần mười của giây)?
Giải bài 10 trang 10 vở thực hành Toán 9 tập 2
Lực F của gió khi thổi vuông góc vào cánh buồm tỉ lệ thuận với bình phương tốc độ v của gió, tức là (F = a{v^2}) (a là hằng số). Biết rằng khi tốc độ gió bằng 3m/s thì lực tác động lên cánh buồm của một chiếc thuyền bằng 270N. a) Tính hằng số a. b) Hỏi khi tốc độ gió (v = 10m/s) thì lực thổi F của gió bằng bao nhiêu? c) Biết rằng cánh buồm chỉ có thể chịu được một áp lực tối đa là 10 000N, hỏi chiếc thuyền đó có thể đi được trong gió bão với tốc độ gió 72km/h không?