 Toán 12 Kết nối tri thức | Giải toán lớp 12 Kết nối tri thức
Toán 12 Kết nối tri thức | Giải toán lớp 12 Kết nối tri thức
 Bài tập cuối chương 4 - Toán 12 Kết nối tri thức
Bài tập cuối chương 4 - Toán 12 Kết nối tri thức
Giải bài tập 4.25 trang 27 SGK Toán 12 tập 2 - Kết nối tri thức
Cho đồ thị hàm số (y = fleft( x right)) trên đoạn (left[ { - 2;2} right]) như Hình 4.32. Biết (intlimits_{ - 2}^{ - 1} {fleft( x right)dx} = intlimits_1^2 {fleft( x right)dx} = frac{{ - 22}}{{15}}) và (intlimits_{ - 1}^1 {fleft( x right)dx} = frac{{76}}{{15}}). Khi đó, diện tích của hình phẳng được tô màu là A. 8. B. (frac{{22}}{{15}}). C. (frac{{32}}{{15}}). D. (frac{{76}}{{15}}).
Đề bài
Cho đồ thị hàm số \(y = f\left( x \right)\) trên đoạn \(\left[ { - 2;2} \right]\) như Hình 4.32.
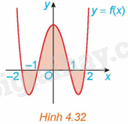
Biết \(\int\limits_{ - 2}^{ - 1} {f\left( x \right)dx} = \int\limits_1^2 {f\left( x \right)dx} = \frac{{ - 22}}{{15}}\) và \(\int\limits_{ - 1}^1 {f\left( x \right)dx} = \frac{{76}}{{15}}\). Khi đó, diện tích của hình phẳng được tô màu là
A. 8.
B. \(\frac{{22}}{{15}}\).
C. \(\frac{{32}}{{15}}\).
D. \(\frac{{76}}{{15}}\).
Phương pháp giải - Xem chi tiết
Sử dụng kiến thức về diện tích hình phẳng giới hạn bởi hai đồ thị hàm số và đường thẳng \(x = a,x = b\) để tính: Diện tích S của hình phẳng giới hạn đồ thị của hai hàm số f(x), g(x) liên tục trên đoạn [a; b] và hai đường thẳng \(x = a,x = b\), được tính bằng công thức \(S = \int\limits_a^b {\left| {f\left( x \right) - g\left( x \right)} \right|dx} \).
Lời giải chi tiết
Diện tích cần tìm là:
\(S = \int\limits_{ - 2}^2 {\left| {f(x)} \right|dx} = \int\limits_{ - 2}^{ - 1} {\left| {f(x)} \right|dx} + \int\limits_{ - 1}^1 {\left| {f(x)} \right|dx} + \int\limits_1^2 {\left| {f(x)} \right|dx} \)
\( = - \int\limits_{ - 2}^{ - 1} {f(x)dx} + \int\limits_{ - 1}^1 {f(x)dx} - \int\limits_1^2 {f(x)dx} = - \left( { - \frac{{22}}{{15}}} \right) + \frac{{76}}{{15}} - \left( { - \frac{{22}}{{15}}} \right) = 8\).
Chọn A
- Giải bài tập 4.26 trang 28 SGK Toán 12 tập 2 - Kết nối tri thức
- Giải bài tập 4.27 trang 28 SGK Toán 12 tập 2 - Kết nối tri thức
- Giải bài tập 4.28 trang 28 SGK Toán 12 tập 2 - Kết nối tri thức
- Giải bài tập 4.29 trang 28 SGK Toán 12 tập 2 - Kết nối tri thức
- Giải bài tập 4.30 trang 28 SGK Toán 12 tập 2 - Kết nối tri thức
>> Xem thêm
Luyện Bài Tập Trắc nghiệm Toán 12 - Kết nối tri thức - Xem ngay
Các bài khác cùng chuyên mục
- Giải câu hỏi mở đầu trang 54 SGK Toán 12 tập 2 - Kết nối tri thức
- Giải câu hỏi mở đầu trang 41 SGK Toán 12 tập 2 - Kết nối tri thức
- Giải câu hỏi mở đầu trang 29 SGK Toán 12 tập 2 - Kết nối tri thức
- Giải câu hỏi mở đầu trang 12 SGK Toán 12 tập 2 - Kết nối tri thức
- Giải câu hỏi mở đầu trang 4 SGK Toán 12 tập 2 - Kết nối tri thức
- Giải câu hỏi mở đầu trang 54 SGK Toán 12 tập 2 - Kết nối tri thức
- Giải câu hỏi mở đầu trang 41 SGK Toán 12 tập 2 - Kết nối tri thức
- Giải câu hỏi mở đầu trang 29 SGK Toán 12 tập 2 - Kết nối tri thức
- Giải câu hỏi mở đầu trang 12 SGK Toán 12 tập 2 - Kết nối tri thức
- Giải câu hỏi mở đầu trang 4 SGK Toán 12 tập 2 - Kết nối tri thức












Danh sách bình luận