Giải bài 9.32 trang 57 sách bài tập toán 9 - Kết nối tri thức tập 2

Cho tam giác nhọn ABC có các đường cao BE, CF. Một đường tròn (O) đi qua hai điểm E, F và cắt các tia đối của hai tia BF, CE lần lượt tại X và Y. Chứng minh rằng XY song song với BC.

Gửi góp ý cho Loigiaihay.com và nhận về những phần quà hấp dẫn

Đề bài

Cho tam giác nhọn ABC có các đường cao BE, CF. Một đường tròn (O) đi qua hai điểm E, F và cắt các tia đối của hai tia BF, CE lần lượt tại X và Y. Chứng minh rằng XY song song với BC.

Phương pháp giải - Xem chi tiết

+ Chứng minh bốn điểm B, E, F, C cùng nằm trên đường tròn có tâm là trung điểm của BC, đường kính BC, suy ra tứ giác BFEC là tứ giác nội tiếp.

+ Chứng minh $\widehat {FBC} = {180^o} - \widehat {FEC} = {180^o} - \widehat {FEY} = \widehat {FXY}$, suy ra XY song song với BC.

Lời giải chi tiết

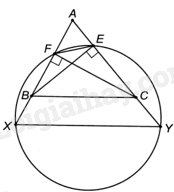
Vì các tam giác vuông BEC, BFC có chung cạnh huyền BC nên bốn điểm B, E, F, C cùng nằm trên đường tròn có tâm là trung điểm của BC và bán kính $\frac{{BC}}{2}$. Do đó, tứ giác BFEC là tứ giác nội tiếp.

Vì tổng các góc đối nhau của các tứ giác nội tiếp BFEC và XFEY bằng 180 độ nên:

$\widehat {FBC} = {180^o} - \widehat {FEC} = {180^o} - \widehat {FEY} = \widehat {FXY}$

Mà hai góc này ở vị trí đồng vị nên XY song song với BC.

Bình luận

Chia sẻ

Bình chọn:

4.9 trên 7 phiếu

Bài tiếp theo

Giải bài 9.31 trang 56 sách bài tập toán 9 - Kết nối tri thức tập 2
Cho hình chữ nhật ABCD nội tiếp đường tròn (O) với AB=3cm; AD=4cm. Vẽ một hình vuông nội tiếp (O). Tính diện tích của hình vuông đó.
Giải bài 9.30 trang 56 sách bài tập toán 9 - Kết nối tri thức tập 2
Cho hình thoi ABCD có AC=8cm, BD=4cm. Gọi M, N, P, Q lần lượt là trung điểm của AB, BC, CD, DA. Chứng minh rằng tứ giác MNPQ nội tiếp một đường tròn và tìm bán kính của đường tròn đó.
Giải bài 9.29 trang 56 sách bài tập toán 9 - Kết nối tri thức tập 2
Cho hình vuông ABCD có cạnh bằng 3cm và nội tiếp đường tròn (O) như Hình 9.8. Tính tổng diện tích của bốn hình viên phân được giới hạn bởi các cạnh hình vuông (phần tô đậm trong hình).
Giải bài 9.28 trang 56 sách bài tập toán 9 - Kết nối tri thức tập 2
Cho hình vuông ABCD có cạnh bằng 4cm. Gọi M, N, P, Q lần lượt là trung điểm của AB, BC, CD, DA. Chứng minh rằng tứ giác MNPQ nội tiếp một đường tròn và tìm bán kính, chu vi của đường tròn đó.
Giải bài 9.27 trang 56 sách bài tập toán 9 - Kết nối tri thức tập 2
a) Nếu một hình bình hành nội tiếp một đường tròn thì hình đó phải là là hình chữ nhật; b) Nếu một hình thoi nội tiếp một đường tròn thì hình đó phải là hình vuông; c) Nếu một hình thang nội tiếp một đường tròn thì hình đó phải là hình thang cân.
Giải bài 9.26 trang 56 sách bài tập toán 9 - Kết nối tri thức tập 2
Cho tứ giác ABCD nội tiếp đường tròn (O), hai đường chéo AC và BD cắt nhau tại điểm J. Chứng minh rằng: a) $Delta JADbacksim Delta JBC,Delta JABbacksim Delta JDC$; b) (frac{{JA}}{{JC}} = frac{{BA}}{{BC}}.frac{{DA}}{{DC}}).
Giải bài 9.25 trang 56 sách bài tập toán 9 - Kết nối tri thức tập 2
Cho tứ giác ABCD nội tiếp đường tròn (O) sao cho hai tia AB và DC cắt nhau tại điểm I. Chứng minh rằng: a) $Delta IADbacksim Delta ICB,Delta IACbacksim Delta IDB$; b) (frac{{IC}}{{ID}} = frac{{AC}}{{AD}}.frac{{BC}}{{BD}}).
Giải bài 9.24 trang 56 sách bài tập toán 9 - Kết nối tri thức tập 2
Cho tứ giác ABCD nội tiếp đường tròn (O) sao cho hai tia AB và DC cắt nhau tại điểm K, hai đường chéo AC và BD cắt nhau tại điểm H. Kí hiệu $oversetfrown{AD}$ là cung AD không chứa điểm B và $oversetfrown{BC}$ là cung BC không chứa A. Chứng minh rằng: a) (widehat {BKC} = frac{1}{2})(sđ$oversetfrown{AD}$-sđ$oversetfrown{BC}$); b) (widehat {BHC} = frac{1}{2})(sđ$oversetfrown{AD}$+sđ$oversetfrown{BC}$).
Giải bài 9.23 trang 55 sách bài tập toán 9 - Kết nối tri thức tập 2
Cho tứ giác ABCD nội tiếp đường tròn (O), hai đường chéo AC và BD cắt nhau tại điểm E. Tính số đo các góc của tứ giác ABCD, biết rằng (widehat {AEB} = {80^o},widehat {ABE} = {70^o}) và (widehat {ECB} = {50^o}).
Giải bài 9.22 trang 55 sách bài tập toán 9 - Kết nối tri thức tập 2
Hãy cho biết số đo các góc còn lại của tứ giác ABCD nội tiếp đường tròn (O) trong mỗi trường hợp sau: a) (widehat {AOB} = {100^o},widehat {BOC} = {120^o},widehat {COD} = {70^o}). b) (widehat {BOC} = {110^o},widehat {COD} = {70^o},widehat {DOA} = {100^o}).
Giải bài 9.21 trang 55 sách bài tập toán 9 - Kết nối tri thức tập 2
Hãy cho biết số đo các góc còn lại của tứ giác nội tiếp ABCD trong mỗi trường hợp sau: a) (widehat A = {80^o},widehat B = {120^o}); b) (widehat B = {70^o},widehat C = {110^o}); c) (widehat C = {110^o},widehat D = {60^o}); d) (widehat D = {65^o},widehat A = {130^o}).