Giải bài 8 trang 88 vở thực hành Toán 9

Giải tam giác ABC vuông tại A, biết a) (BC = 20,widehat C = {40^o}); b) (AC = 82,widehat B = {55^o}); c) (BC = 32,AC = 20). (Kết quả về cạnh làm tròn đến chữ số thập phân thứ nhất, kết quả về góc làm tròn đến độ).

Tổng hợp Đề thi vào 10 có đáp án và lời giải

Toán - Văn - Anh

Đề bài

Giải tam giác ABC vuông tại A, biết

a) \(BC = 20,\widehat C = {40^o}\);

b) \(AC = 82,\widehat B = {55^o}\);

c) \(BC = 32,AC = 20\).

(Kết quả về cạnh làm tròn đến chữ số thập phân thứ nhất, kết quả về góc làm tròn đến độ).

Phương pháp giải - Xem chi tiết

a) Ta có: \(\widehat B = {90^o} - \widehat C\); \(AC = BC.\cos C\); \(AB = BC.\sin C\).

b) Ta có: \(\widehat C = {90^o} - \widehat B\); \(AB = AC.\tan C\); \(B{C^2} = A{B^2} + A{C^2}\) nên tính được BC.

c) Ta có: \(A{B^2} = B{C^2} - A{B^2}\) tính được AB; \(\sin B = \frac{{AC}}{{BC}}\) tính được góc B; \(\widehat C = {90^o} - \widehat B\)

Lời giải chi tiết

a) (H.4.31)

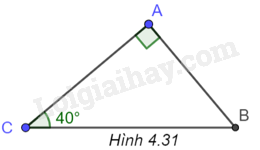
Ta có: \(\widehat B = {90^o} - \widehat C = {50^o}\),

\(AC = BC.\cos C = 20.\cos {40^o} \approx 15,3\), \(AB = BC.\sin C = 20.\sin {40^o} \approx 12,9\)

b) (H.4.32)

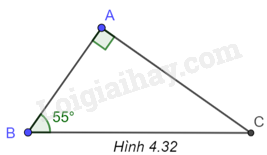
Ta có: \(\widehat C = {90^o} - \widehat B = {35^o}\).

\(AB = AC.\tan C = 82.\tan {35^o} \approx 57,4\)

\(B{C^2} = A{B^2} + A{C^2} = {82^2} + {57,4^2}\), suy ra \(BC = 100,1\)

c) (H.4.33)

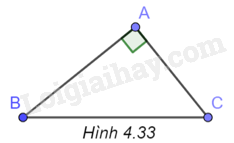
Ta có: \(A{B^2} = B{C^2} - A{B^2} = {32^2} - {20^2}\), suy ra \(AB \approx 25,0\)

\(\sin B = \frac{{AC}}{{BC}} = \frac{{20}}{{32}} = 0,625\), suy ra \(\widehat B \approx {39^o}\)

Từ đó suy ra \(\widehat C = {90^o} - \widehat B = {51^o}\)

Bình luận

Chia sẻ

Bình chọn:

4.9 trên 7 phiếu

Bài tiếp theo

Giải bài 7 trang 88 vở thực hành Toán 9
Trong một buổi tập trận, một tàu ngầm đang ở trên mặt biển bắt đầu di chuyển theo đường thẳng tạo với mặt nước biển một góc ({21^o}) để lặn xuống (H.4.30). a) Khi tàu chuyển động theo hướng đó và đi được 200m thì tàu ở độ sâu bao nhiêu so với mặt nước biển)? (làm tròn đến m). b) Giả sử tốc độ của tàu là 9km/h thì sau bao lâu (tính từ lúc bắt đầu lặn) tàu ở độ sâu 200m (tức là cách mặt nước biển 200m)?
Giải bài 9 trang 89 vở thực hành Toán 9
Cho tam giác ABC vuông ở A và BD là tia phân giác góc B. Biết (widehat C = {42^o},AB = 22), tính độ dài BD, AD, DC (làm tròn đến chữ số thập phân thứ nhất).
Giải bài 6 trang 87 vở thực hành Toán 9
Mặt cắt ngang của một đập ngăn nước có dạng hình thang ABCD (H.4.29a). Chiều rộng của mặt trên AB của đập là 3m. Độ dốc của sườn AD, tức là (tan D = 1,25). Độ dốc của sườn BC, tức là (tan C = 1,5). Chiều cao của đập là 3,5m. Hãy tính chiều rộng CD của chân đập, chiều dài của các sườn AD và BC (làm tròn đến dm).
Giải bài 5 trang 87 vở thực hành Toán 9
Một bạn muốn tính khoảng cách giữa hai địa điểm A, B ở hai bên hồ nước. Biết rằng các khoảng cách từ một điểm C đến A và đến B là (CA = 90m,CB = 150m) và (widehat {ACB} = {120^o}) (H.4.28). Hãy tính AB giúp bạn.
Giải bài 4 trang 86 vở thực hành Toán 9
Tính các số liệu còn thiếu (dấu “?”) ở Hình 4.26 với góc làm tròn đến độ, với độ dài làm tròn đến chữ số thập phân thứ nhất.
Giải bài 3 trang 85 vở thực hành Toán 9
Tìm chiều rộng d của dòng sông trong Hình 4.25a (làm tròn đến m).
Giải bài 2 trang 85 vở thực hành Toán 9
Cho tam giác ABC có chân đường cao AH nằm giữa B và C. Biết (HB = 3cm,HC = 6cm,widehat {HAC} = {60^o}). Hãy tính độ dài các cạnh (làm tròn đến cm), số đo các góc của tam giác ABC (làm tròn đến độ).
Giải bài 1 trang 84 vở thực hành Toán 9
Một cuốn sách khổ (17 times 24cm), tức là chiều rộng 17cm, chiều dài 24cm. Gọi (alpha ) là góc giữa đường chéo và cạnh 17cm. Tính (sin alpha ,cos alpha ) (làm tròn đến chữ số thập phân thứ hai) và tính số đo (alpha ) (làm tròn đến độ).