Giải bài 53 trang 124 sách bài tập toán 9 - Cánh diều tập 1

Cho ba đường tròn (A; 10 cm), (B; 15 cm), (C; 15 cm) tiếp xúc ngoài với nhau đôi một. Đường tròn (A) tiếp xúc với (B) và (C) lần lượt tại C' và B'. Đường tròn (B) tiếp xúc với (C) tại A' (Hình 53). a) Chứng minh AA' là tiếp tuyến chung của đường tròn (B) và (C). b) Tính độ dài đoạn thẳng AA′ và diện tích tam giác AB'C'.

Đề bài

Cho ba đường tròn (A; 10 cm), (B; 15 cm), (C; 15 cm) tiếp xúc ngoài với nhau đôi một. Đường tròn (A) tiếp xúc với (B) và (C) lần lượt tại C' và B'. Đường tròn (B) tiếp xúc với (C) tại A' (Hình 53).

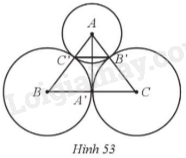
a) Chứng minh AA' là tiếp tuyến chung của đường tròn (B) và (C).

b) Tính độ dài đoạn thẳng AA′ và diện tích tam giác AB'C'.

Phương pháp giải - Xem chi tiết

a) Bước 1: Chứng minh A thuộc đường trung trực của BC (do \(AB = AC\)).

Bước 2: Chứng minh \(A'\) thuộc đường trung trực của BC (do\(BA' = CA'\)).

b) Bước 1: Tính \(AA'\): Áp dụng định lý Pythagore trong tam giác \(AA'B\).

Bước 2: Chứng minh \(B'C'//BC\) (áp dụng định lý Thales trong tam giác ABC), từ đó tính được B’C’.

Bước 3: Áp dụng định lý Thales trong tam giác ACA’ để tính AH.

Bước 4: Chứng minh \(AH \bot C'B'\) và tính diện tích tam giác AB’C’.

Lời giải chi tiết

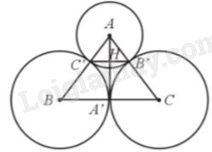
a) Ta có: \(AC' = AB' = 10\)cm (bán kính (A)),

\(BC' = BA' = 15\)cm (bán kính (B)),

\(CA' = CB' = 15\)cm (bán kính (C)).

Do \(AB = BC' + AC' = 15 + 10 = 25\)cm và \(AC = CB' + AB' = 15 + 10 = 25\)cm nên \(AB = AC\), do đó A thuộc đường trung trực của BC.

Mà \(BA' = CA' = 15\)cm nên \(A'\) thuộc đường trung trực của BC.

Suy ra \(AA'\) đường trung trực của BC, nên \(AA' \bot BC\) tại A’

Vậy \(AA'\) là tiếp tuyến chung của (B) và (C).

b) Áp dụng định lý Pythagore trong tam giác vuông \(AA'B\) có:

\(AA' = \sqrt {A{B^2} - BA{'^2}} = \sqrt {{{25}^2} - 15{'^2}} = 20\)cm.

Gọi H là giao điểm của AA’ và B’C’.

Ta có \(BC = BA' + CA' = 15 + 15 = 30\)cm.

Xét tam giác ABC có \(\frac{{AC'}}{{AB}} = \frac{{AB'}}{{AC}} = \frac{{10}}{{25}}\) nên \(B'C'//BC\) (định lý Thales đảo).

Do đó \(\frac{{B'C'}}{{BC}} = \frac{{AB'}}{{AC}}\) hay \(B'C' = \frac{{BC.AB'}}{{AC}} = \frac{{30.10}}{{25}} = 12\)cm.

Xét tam giác ACA’ có \(HB'//CA'\) nên \(\frac{{AH}}{{AA'}} = \frac{{AB'}}{{AC}}\) (định lý Thales) hay \(AH = \frac{{AB'.AA'}}{{AC}} = \frac{{10.20}}{{25}} = 8\)cm.

Ta có \(B'C'//BC,AA' \bot BC\) nên \(B'C' \bot AA'\) hay \(AH \bot C'B'\).

Diện tích tam giác \(AB'C'\) là \(\frac{1}{2}B'C'.AH = \frac{1}{2}.12.8 = 48\)cm².

Bình luận

Chia sẻ

Bình chọn:

4.9 trên 7 phiếu

Bài tiếp theo

Giải bài 54 trang 124 sách bài tập toán 9 - Cánh diều tập 1
Cho đường tròn (O; R) và ba điểm A, B, C nằm trên đường tròn với AB < AC. Gọi M là trung điểm của đoạn thẳng BC. Trên cung BC không chứa điểm A, lấy điểm D sao cho \(\widehat {BAD} = \widehat {CAM}\). a) Chứng minh \(\widehat {ADB} = \widehat {CDM}\). b) Gọi E là giao điểm của tia OM và cung BC. Tính diện tích hình quạt tròn giới hạn bởi các bán kính OE, OC và cung nhỏ CE theo R, biết \(BC = R\sqrt 2 \).
Giải bài 55 trang 124 sách bài tập toán 9 - Cánh diều tập 1
Cho nửa đường tròn tâm O đường kính AB. Gọi C, D lần lượt là điểm chính giữa của cung AB, AC. a) Chứng minh \(\widehat {BAC} = \widehat {COD} = \widehat {ABC} = \widehat {ACO}\). b) Lấy điểm M thuộc cung CD. Chứng minh \(AM > CM\)và \(\widehat {COM} = 2\widehat {CAM}\). c) Khi M di chuyển trên cung nhỏ AC, tìm vị trí của điểm M để diện tích của tam giác MAC lớn nhất.
Giải bài 56 trang 124 sách bài tập toán 9 - Cánh diều tập 1
Thành phố Hồ Chí Minh có vĩ độ là 10°10′ Bắc. Tìm độ dài cung kinh tuyến từ Thành phố Hồ Chí Minh đến Xích Đạo (làm tròn kết quả đến hàng trăm của kilômét), biết mỗi kinh tuyến là một nửa vòng Trái Đất và có độ dài khoảng 20 000 km.
Giải bài 57 trang 124 sách bài tập toán 9 - Cánh diều tập 1
Cho hình thang vuông ABCD (\(\widehat A = \widehat B = 90^\circ \)) với \(\widehat C = 30^\circ \), BC = CD = a. Vẽ một phần đường tròn (C; CD) (Hình 54). Tính diện tích của phần tô màu xám theo a.
Giải bài 58 trang 125 sách bài tập toán 9 - Cánh diều tập 1
Cho hình vành khuyên giới hạn bởi hai đường tròn (O; R), (O; r) với \(R + r = 1,2dm\), \(R > r\)và diện tích hình vành khuyên đó là 1,5072 dm2 (Hình 55). Tính R và r, \(\pi \approx 3,14\).
Giải bài 59 trang 125 sách bài tập toán 9 - Cánh diều tập 1
Tam giác Reuleaux là hình tạo nên từ phần giao nhau của ba đường tròn cùng bán kính, tâm của mỗi đường tròn chính là giao điểm của hai đường tròn còn lại. Tạo tam giác Reuleaux từ ba đường tròn (A), (B), (C) (Hình 56). Tính số đo các cung nhỏ BaC, CbA, AcB của tam giác Reuleaux. Nêu nhận xét về số đo của các cung tròn đó.
Giải bài 60 trang 125 sách bài tập toán 9 - Cánh diều tập 1
Cho đường tròn (O; R) và hai điểm A, B nằm trên đường tròn sao cho độ dài cung nhỏ AB bằng \(\frac{{5\pi R}}{6}\) a) Xác định điểm C trên cung lớn AB sao cho khi kẻ CH vuông góc với AB tại H thì AH = CH. b) Tính độ dài các cung AC, BC theo R. c) Kẻ OK vuông góc với AB tại K, tia OK cắt đường tròn (O) tại E. Tính diện tích hình quạt tròn EOB (giới hạn bởi cung nhỏ BE và hai bán kính OE, OB) theo R. d) Tính tỉ số phần trăm giữa diện tích hình quạt tròn BOC (giới hạn bởi cung nhỏ BC và hai bán
Giải bài 52 trang 123 sách bài tập toán 9 - Cánh diều tập 1
Cho đường tròn tâm O đường kính AB và điểm M di chuyển trên đường tròn (M khác A và B). Vẽ đường tròn (M) tiếp xúc với AB tại H. Từ A và B kẻ hai tiếp tuyến AC, BD của đường tròn (M) lần lượt tại C, D. a) Chứng minh AC + BD không đổi khi M di chuyển trên đường tròn (O). b) Chứng minh CD là tiếp tuyến của đường tròn (O).
Giải bài 51 trang 123 sách bài tập toán 9 - Cánh diều tập 1
Diện tích hình vành khuyên tạo bởi hai đường tròn (O; 12 cm) và (O; 7 cm) là: A. 95π cm2. B. 193π cm2. C. 5π cm2. D. 19π cm2.
Giải bài 50 trang 123 sách bài tập toán 9 - Cánh diều tập 1
Trong 20 giây, bánh xe của một chiếc xe máy quay được 80 vòng. Độ dài bán kính của bánh xe đó là 25 cm. Khi đó, quãng đường xe máy đi được trong 3 phút là: A. 36 000\(\pi \) m. B. 360\(\pi \) m. C. 18 000\(\pi \) m. D. 180\(\pi \) m.
Giải bài 49 trang 123 sách bài tập toán 9 - Cánh diều tập 1
Cho hai đường tròn (O; R) và (O’; R) cắt nhau tại hai điểm M, N với OO' = 24cm và MN = 10 cm (Hình 52). Khi đó, R bằng A. 26 cm. B. 13 cm. C. 14 cm. D. 34 cm
Giải bài 48 trang 123 sách bài tập toán 9 - Cánh diều tập 1
Ở Hình 5, cho hai hình chóp tứ giác đều S.ABCD và S’.A’B’C’D’ có cùng chiều cao SH= S’H = 30 cm. Thể tích của hình chóp S.ABCD nhỏ hơn thể tích của hình chóp S’A’B’C’D' là 240 cm3. Tính độ dài cạnh đáy của mỗi hình chóp, biết \(A'B' - AB = 2\)cm.
Giải bài 47 trang 123 sách bài tập toán 9 - Cánh diều tập 1
Trên mặt phẳng toạ độ Oxy, cho điểm A(1; 1). Khi đó, đường tròn (A;1) A. Tiếp xúc với trục Ox và cắt trục Oy tại 2 điểm phân biệt. B. Tiếp xúc với trục Oy và cắt trục Ox tại 2 điểm phân biệt. C. Tiếp xúc với cả hai trục Ox và trục Oy. D. Đi qua gốc toạ độ O.