Giải bài 5.24 trang 68 sách bài tập toán 9 - Kết nối tri thức tập 1

Cho điểm A và đường tròn (O; R) sao cho (R < OA < 3R). a) Chứng minh rằng đường tròn (A; 2R) cắt đường tròn (O; R). Gọi B là một trong hai giao điểm của chúng. b) Gọi C là điểm đối xứng với B qua O. Nối A với C cắt (O) tại D (khác C). Chứng minh rằng (AD = DC).

Đề bài

Cho điểm A và đường tròn (O; R) sao cho \(R < OA < 3R\).

a) Chứng minh rằng đường tròn (A; 2R) cắt đường tròn (O; R). Gọi B là một trong hai giao điểm của chúng.

b) Gọi C là điểm đối xứng với B qua O. Nối A với C cắt (O) tại D (khác C). Chứng minh rằng \(AD = DC\).

Phương pháp giải - Xem chi tiết

a) Chứng minh \(2R - R < OA < 2R + R\) nên đường tròn (A; 2R) cắt đường tròn (O; R).

b) + Sử dụng tính đối xứng của đường tròn và do C đối xứng với B qua O, ta có \(C \in \left( O \right)\).

+ Chứng minh tam giác BCD vuông tại D, suy ra \(BD \bot CD\).

+ Chứng minh tam giác ABC cân tại B, BD là đường cao đồng thời là trung tuyến. Do đó, \(AD = DC\).

Lời giải chi tiết

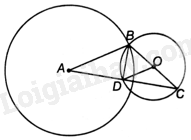
a) Vì \(R < OA < 3R\) nên \(2R - R < OA < 2R + R\) nên đường tròn (A; 2R) cắt đường tròn (O; R).

b) Do tính đối xứng của đường tròn và do C đối xứng với B qua O, ta có \(C \in \left( O \right)\).

Do đó, BC là một đường kính của (O; R).

Lại có, AB là một bán kính của (A; 2R).

Suy ra, \(BC = 2R = AB\).

Suy ra tam giác ABC cân tại B.

Mặt khác, tam giác BCD có DO là trung tuyến và \(DO = \frac{{BC}}{2}\) nên tam giác BCD vuông tại D.

Suy ra: \(BD \bot CD\).

Tam giác ABC cân tại B nên BD vừa là đường cao vừa là đường trung tuyến. Do đó, \(AD = DC\).

Bình luận

Chia sẻ

Bình chọn:

4.9 trên 7 phiếu

Bài tiếp theo

Giải bài 5.25 trang 68 sách bài tập toán 9 - Kết nối tri thức tập 1
Cho I là trung điểm của đoạn AB. Xét các đường tròn (I; IB) và (A; AB). a) Hai đường tròn (I) và (A) nói trên có vị trí tương đối như thế nào? b) Đường thẳng đi qua B, cắt các đường tròn (I) và (A) lần lượt tại C và D. Hãy so sánh các độ dài BC và CD.
Giải bài 5.26 trang 68 sách bài tập toán 9 - Kết nối tri thức tập 1
Cho tam giác ABC. a) Chứng minh rằng hai đường tròn (B; BA) và (C; CA) cắt nhau. Gọi A’ là giao điểm khác A của hai đường tròn đó. b) Chứng minh rằng A và A’ đối xứng nhau qua BC. c) Biết rằng (AA' = 24cm,AB = 15cm) và (AC = 13cm). Tính độ dài BC.
Giải bài 5.23 trang 68 sách bài tập toán 9 - Kết nối tri thức tập 1
Vẽ hình và chứng minh phần b của Ví dụ 2. Cho đường tròn (O) và dây AB không là đường kính của (O). a) Gọi O' là một điểm tùy ý nằm giữa O và A. Đường thẳng đi qua O' và song song với OB cắt AB tại C. Hãy xác định vị trí tương đối của (O) và (O'; O'C). b) Vị trí tương đối của (O) và (O'; O'C) sẽ như thế nào nếu O' thẳng hàng với O và A, nhưng nằm ngoài đoạn OA?
Giải bài 5.22 trang 68 sách bài tập toán 9 - Kết nối tri thức tập 1
Hai đường tròn (O; 2cm) và (O’; 3cm) có vị trí tương đối như thế nào trong mỗi trường hợp sau: a) (OO' = 4cm)? b) (OO' = 5cm)? c) (OO' = 6cm)?