Giải bài 5 trang 29 Chuyên đề học tập Toán 11 Chân trời sáng tạo

Cho hai tam giác vuông cân OAB và OA’B’ có chung đỉnh O sao cho O nằm trên đoạn AB’ và nằm ngoài đoạn A’B

Tổng hợp đề thi học kì 1 lớp 11 tất cả các môn - Chân trời sáng tạo

Toán - Văn - Anh - Lí - Hóa - Sinh

Đề bài

Cho hai tam giác vuông cân OAB và OA’B’ có chung đỉnh O sao cho O nằm trên đoạn AB’ và nằm ngoài đoạn A’B. Gọi G và G’ lần lượt là trọng tâm của \(\Delta \)OAA’ và \(\Delta \)OBB’. Chứng minh rằng \(\Delta \)OGG’ là tam giác vuông cân.

Phương pháp giải - Xem chi tiết

Tam giác vuông cân là tam giác có một góc bằng \({90^o}\) và 2 cạnh góc vuông bằng nhau.

Lời giải chi tiết

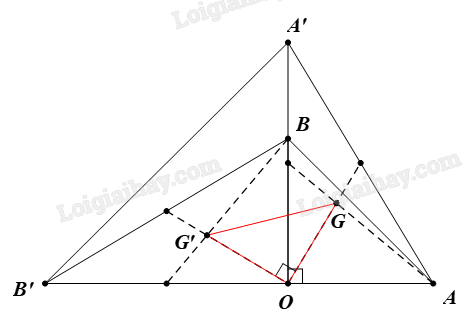
Do DOAB là tam giác vuông cân nên OA = OB và \(\widehat {AOB} = 90^\circ \)

Do DOA’B’ là tam giác vuông cân nên OA’ = OB’ và \(\widehat {A'OB'} = 90^\circ \)

Phép quay tâm O, góc quay 90° biến:

⦁ Điểm O thành điểm O;

⦁ Điểm A thành điểm B;

⦁ Điểm A’ thành điểm B’.

Do đó ảnh của \(\Delta \) OAA’ qua phép quay tâm O, góc quay 90° là \(\Delta \) OBB’.

Mà G, G’ lần lượt là trọng tâm của \(\;\Delta OAA',{\rm{ }}\Delta OBB'.\)

Vì vậy ảnh của G qua phép quay tâm O, góc quay 90° là G’.

Suy ra \(OG{\rm{ }} = {\rm{ }}OG'\) và \(\widehat {GOG'} = \left( {OG,OG'} \right) = 90^\circ \)

DOGG’ có \(OG{\rm{ }} = {\rm{ }}OG'\) và \(\widehat {GOG'} = 90^\circ \) nên là tam giác vuông cân tại O.

Vậy \(\Delta OGG'\) vuông cân tại O.

Bình luận

Chia sẻ

Bình chọn:

3.8 trên 5 phiếu

Bài tiếp theo

Giải bài 4 trang 29 Chuyên đề học tập Toán 11 Chân trời sáng tạo
Chỉ ra phép quay có thể biến mỗi hình trong Hình 10 thành chính nó.
Giải bài 2 trang 29 Chuyên đề học tập Toán 11 Chân trời sáng tạo
Cho hai tam giác đều ABC và AB’C’ như Hình 9. Gọi M, N lần lượt là trung điểm của BB’ và CC’. Chứng minh ∆AMN đều.
Giải bài 1 trang 28 Chuyên đề học tập Toán 11 Chân trời sáng tạo
Trong mặt phẳng tọa độ Oxy, cho các điểm \(A\left( {-4;{\rm{ }}2} \right),{\rm{ }}B\left( {-4;{\rm{ }}5} \right)\) và \(C\left( {-1;{\rm{ }}3} \right).\)
Giải mục 2 trang 27, 28 Chuyên đề học tập Toán 11 - Chân trời sáng tạo
Cho phép quay Q(O; φ) và hai điểm tùy ý A, B (O, A, B không thẳng hàng) như Hình 6. Vẽ A’, B’ là ảnh của A, B qua phép quay. Hai tam giác OAB và OA’B’ có bằng nhau không?
Giải mục 1 trang 25, 26, 27 Chuyên đề học tập Toán 11 - Chân trời sáng tạo
Tìm phép biến hình biến \(\Delta \)BAC thành \(\Delta \)BA’C’ (Hình 1).
Giải khởi động trang 25 Chuyên đề học tập Toán 11 - Chân trời sáng tạo
Vẽ mỗi hình sau ra một tờ giấy, cắt rời mỗi hình theo hình tròn. Tìm một điểm O trên mỗi hình