Giải bài 4.37 trang 53 sách bài tập toán 9 - Kết nối tri thức tập 1

Một người đứng cách chân ngọn hải đăng 50m, nhìn xuống chân hải đăng dưới góc ({2^o}) và nhìn lên đỉnh ngọn hải đăng dưới góc ({45^o}) (so với phương nằm ngang) (H.4.22). Tính chiều cao ngọn hải đăng (làm tròn đến mét).

Đề bài

Một người đứng cách chân ngọn hải đăng 50m, nhìn xuống chân hải đăng dưới góc \({2^o}\) và nhìn lên đỉnh ngọn hải đăng dưới góc \({45^o}\) (so với phương nằm ngang) (H.4.22). Tính chiều cao ngọn hải đăng (làm tròn đến mét).

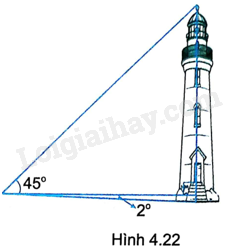
Phương pháp giải - Xem chi tiết

+ Gọi chân hải đăng ở vị trí điểm A, đỉnh hải đăng ở vị trí điểm B, đầu người quan sát ở vị trí điểm C,

H là hình chiếu vuông góc của C trên đường thẳng AB.

+ Chỉ ra H nằm giữa A và B.

+ Tam giác ACH vuông tại H nên \(AH = CH\tan {2^o}\).

+ Chứng minh tam giác BCH vuông cân tại H nên \(HB = HC\).

+ \(AB = AH + HB\) nên tính được AB.

Lời giải chi tiết

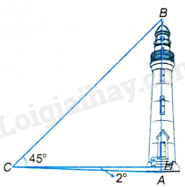
Gọi chân hải đăng ở vị trí điểm A, đỉnh hải đăng ở vị trí điểm B, đầu người quan sát ở vị trí điểm C.

Gọi H là hình chiếu vuông góc của C trên đường thẳng AB thì theo giả thiết, ta có H nằm giữa A và B, \(CH = 50m\).

Tam giác ACH vuông tại H, \(\widehat {ACH} = {2^o}\) nên \(AH = CH\tan {2^o} = 50\tan {2^o}\)

Tam giác CBH vuông tại H, \(\widehat {BCH} = {45^o}\) nên tam giác CBH vuông cân tại H, do đó \(HB = HC = 50m\)

Suy ra \(AB = AH + HB = 50\left( {\tan {2^o} + 1} \right) \approx 52\left( m \right)\)

Bình luận

Chia sẻ

Bình chọn:

4.9 trên 7 phiếu

Giải bài 4.36 trang 53 sách bài tập toán 9 - Kết nối tri thức tập 1
Tìm độ dài dây cáp mắc giữa hai cọc ở vị trí C, D trên hai bên bờ vực như trong Hình 4.21 (làm tròn đến mét).
Giải bài 4.35 trang 52 sách bài tập toán 9 - Kết nối tri thức tập 1
Hai chiếc thuyền A và B ở vị trí được minh họa như trong Hình 4.20. Tính khoảng cách giữa chúng (làm tròn đến m), biết (IK = 380m).
Giải bài 4.34 trang 52 sách bài tập toán 9 - Kết nối tri thức tập 1
Một cầu thủ đứng cách khung thành 18m, đá quả bóng sát mặt đất, nghiêng một góc ({20^o}) so với phương vuông góc với khung thành, tới điểm M của khung thành (H.4.19). Tính khoảng cách từ cầu thủ đến điểm M (làm tròn đến dm).
Giải bài 4.33 trang 52 sách bài tập toán 9 - Kết nối tri thức tập 1
Tính khoảng cách giữa hai địa điểm A, B ở hai bên hồ nước (không đo trực tiếp được), biết khoảng cách từ một địa điểm C đến A và đến B là (CA = 90m), (CB = 150m,;widehat {CAB} = {120^o}) (làm tròn đến m) (H.4.18).
Giải bài 4.32 trang 52 sách bài tập toán 9 - Kết nối tri thức tập 1
Cho tam giác ABC có đường cao AH, (widehat B = {60^o},widehat C = {45^o}) và cạnh (BC = 6cm). Chứng minh rằng (AH = 3left( {3 - sqrt 3 } right)cm).
Giải bài 4.31 trang 51 sách bài tập toán 9 - Kết nối tri thức tập 1
Chiều cao từ mặt đất đến đỉnh tháp Pisa ở Italia là 58m, tháp nghiêng góc ({5^o}30') đối với phương thẳng đứng (H.4.17). Khi Mặt Trời chiếu vuông góc với mặt đất thì bóng của tháp dài bao nhiêu decimét?
Giải bài 4.30 trang 51 sách bài tập toán 9 - Kết nối tri thức tập 1
Cho hai tòa nhà cách nhau 32m. Tại điểm A trên nóc tòa nhà cao nhìn xuống nóc D và chân C của tòa nhà thấp lần lượt theo các góc ({15^o}) và ({43^o}) (so với phương nằm ngang) (H.4.16). Tính chiều cao của hai tòa nhà đó (làm tròn đến m).
Giải bài 4.29 trang 51 sách bài tập toán 9 - Kết nối tri thức tập 1
Xét điểm B nằm giữa hai điểm A và H. Giả sử có điểm D sao cho DH vuông góc với AB và (widehat {DAH} = {15^o},widehat {DBH} = {30^o}). Chứng minh rằng (HD = frac{{AB}}{2}).
Giải bài 4.28 trang 51 sách bài tập toán 9 - Kết nối tri thức tập 1
Chứng minh nếu một góc nhọn của một tam giác vuông có số đo gấp đôi số đo góc nhọn kia thì tam giác đó có một cạnh dài gấp đôi một trong hai cạnh còn lại.
Giải câu hỏi trắc nghiệm trang 50, 51 sách bài tập toán 9 - Kết nối tri thức tập 1
Tam giác ABC vuông tại A thì: A. (sin B + cos C = 0). B. (sin C + cos B = 0). C. (sin B - cos C = 0). D. (cos B + cos C = 0).