 SBT Toán 9 - giải SBT Toán 9 - Kết nối tri thức với cuộc sống
SBT Toán 9 - giải SBT Toán 9 - Kết nối tri thức với cuộc sống
 Bài 12. Một số hệ thức giữa cạnh, góc trong tam giác vu..
Bài 12. Một số hệ thức giữa cạnh, góc trong tam giác vu..
Giải bài 4.18 trang 48 sách bài tập toán 9 - Kết nối tri thức tập 1
Cho tam giác ABC vuông tại A với đường cao AH. Hãy tính cosC theo hai cách và suy ra (A{C^2} = BC.HC).
Đề bài
Cho tam giác ABC vuông tại A với đường cao AH. Hãy tính cosC theo hai cách và suy ra \(A{C^2} = BC.HC\).
Phương pháp giải - Xem chi tiết
Xét tam giác ABC vuông tại A có góc nhọn B bằng \(\alpha \) thì tỉ số giữa cạnh kề và cạnh huyền gọi là cos của \(\alpha \).
Lời giải chi tiết
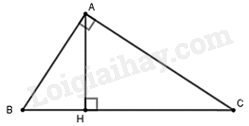
Tam giác ABC vuông tại A nên \(\cos C = \frac{{AC}}{{BC}}\).
Tam giác AHC vuông tại H nên \(\cos C = \frac{{HC}}{{AC}}\).
Do đó, \(\frac{{AC}}{{BC}} = \frac{{HC}}{{AC}}\) nên \(A{C^2} = BC.HC\).
- Giải bài 4.19 trang 48 sách bài tập toán 9 - Kết nối tri thức tập 1
- Giải bài 4.20 trang 48, 49 sách bài tập toán 9 - Kết nối tri thức tập 1
- Giải bài 4.21 trang 49 sách bài tập toán 9 - Kết nối tri thức tập 1
- Giải bài 4.22 trang 49 sách bài tập toán 9 - Kết nối tri thức tập 1
- Giải bài 4.23 trang 49 sách bài tập toán 9 - Kết nối tri thức tập 1
>> Xem thêm
Luyện Bài Tập Trắc nghiệm Toán 9 - Kết nối tri thức - Xem ngay
Các bài khác cùng chuyên mục
- Giải bài 18 trang 74 sách bài tập toán 9 - Kết nối tri thức tập 2
- Giải bài 17 trang 74 sách bài tập toán 9 - Kết nối tri thức tập 2
- Giải bài 16 trang 74 sách bài tập toán 9 - Kết nối tri thức tập 2
- Giải bài 15 trang 74 sách bài tập toán 9 - Kết nối tri thức tập 2
- Giải bài 14 trang 73 sách bài tập toán 9 - Kết nối tri thức tập 2
- Giải bài 18 trang 74 sách bài tập toán 9 - Kết nối tri thức tập 2
- Giải bài 17 trang 74 sách bài tập toán 9 - Kết nối tri thức tập 2
- Giải bài 16 trang 74 sách bài tập toán 9 - Kết nối tri thức tập 2
- Giải bài 15 trang 74 sách bài tập toán 9 - Kết nối tri thức tập 2
- Giải bài 14 trang 73 sách bài tập toán 9 - Kết nối tri thức tập 2











