Giải bài 4 trang 34 sách bài tập toán 10 - Chân trời sáng tạo
Cho biết mỗi kilogam thịt bò giá 250 nghìn đồng, trong đó có chứa khoảng 800 đơn vị protein và 100 đơn vị lipit, mỗi kilogam thịt heo có giá 200 nghìn đồng, trong đo có chứa khoảng 600 đơn vị protein và 200 đơn vị lipit.
Tổng hợp đề thi học kì 1 lớp 10 tất cả các môn - Chân trời sáng tạo
Toán - Văn - Anh - Lí - Hóa - Sinh - Sử - Địa...
Đề bài
Cho biết mỗi kilogam thịt bò giá 250 nghìn đồng, trong đó có chứa khoảng 800 đơn vị protein và 100 đơn vị lipit, mỗi kilogam thịt heo có giá 200 nghìn đồng, trong đo có chứa khoảng 600 đơn vị protein và 200 đơn vị lipit. Một gia đình cần ít nhất 800 đơn vị protein và 200 đơn vị lipit trong khẩu phần thức ăn mỗi ngày và họ chỉ có thể mua một ngày không quá 1 kg thịt bò và 1,5 kg thịt heo. Hỏi gia đình này phải mua bao nhiêu kilogam thịt mỗi loại để chi phí là ít nhất
Lời giải chi tiết
Gọi x,y là số kilogam thịt bò và thịt lợn mà gia đình đó mua.
Ta có hệ bất phương trình mô tả các điều kiện ràng buộc:
\(\left\{ \begin{array}{l}800x + 600y \ge 800\\100x + 200y \ge 200\\0 \le x \le 1\\0 \le y \le 1,5\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}4x + 3y \ge 4\\x + 2y \ge 2\\x \ge 0\\x \le 1\\y \ge 0\\y \le 1,5\end{array} \right.\)
Biểu diễn miền nghiệm của hệ phương trình trên hệ trục tọa độ Oxy ta được miền nghiệm đa giác ABCDE. Tọa độ các đỉnh của đa giác như hình vẽ:
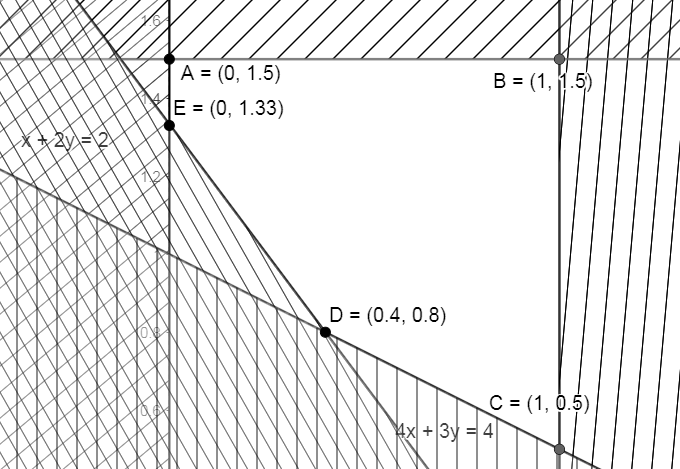
Gọi F là chi phí gia đình sử dụng mua thịt (đơn vị: nghìn đồng), ta có: \(F = 250x + 200y\)
Ta phải tìm x, y thỏa mãn hệ bất phương trình sao cho F nhỏ nhất, nghĩa là tìm giá trị nhỏ nhất của \(F = 250x + 200y\) trên miền đa giác ABCDE
Tính các giá trị của biểu thức F tại các đỉnh của đa giác, ta có:
Tại \(A\left( {0;\frac{3}{2}} \right)\): \(F = 250.0 + 200.\frac{3}{2} = 300\)
Tại \(B\left( {1;\frac{3}{2}} \right)\): \(F = 250.1 + 200.\frac{3}{2} = 550\)
Tại \(C\left( {1;\frac{1}{2}} \right)\): \(F = 250.1 + 200.\frac{1}{2} = 350\)
Tại \(D\left( {\frac{2}{5};\frac{4}{5}} \right)\): \(F = 250.\frac{2}{5} + 200.\frac{4}{5} = 260\)
Tại \(E\left( {0;\frac{4}{3}} \right)\): \(F = 250.0 + 200.\frac{4}{3} \simeq 266,67\)
Vậy ta thấy tại đỉnh \(D\left( {\frac{2}{5};\frac{4}{5}} \right)\) thì giá trị F nhỏ nhất
Vậy khi gia đình đó mua 0,4 kg thịt bò và 0,8 kg thịt lợn mỗi ngày để vẫn đủ lượng protein và lipit và chi phí nhỏ nhất là 260 nghìn đồng
Luyện Bài Tập Trắc nghiệm Toán 10 - Chân trời sáng tạo - Xem ngay












