Giải bài 4 trang 121 vở thực hành Toán 9

Cho hai đường tròn (O) và (O’) tiếp xúc ngoài tại A và cùng tiếp xúc với đường thẳng d tại B và C (khác A), trong đó (B in left( O right)) và (C in left( {O'} right)). Tiếp tuyến của (O) tại A cắt BC tại M. Chứng minh rằng: a) Đường thẳng MA tiếp xúc với (O’); b) Điểm M là trung điểm của đoạn thẳng BC từ đó suy ra ABC là tam giác vuông.

Tổng hợp đề thi học kì 1 lớp 9 tất cả các môn - Kết nối tri thức

Toán - Văn - Anh - KHTN - Lịch sử và Địa lí

Đề bài

Cho hai đường tròn (O) và (O’) tiếp xúc ngoài tại A và cùng tiếp xúc với đường thẳng d tại B và C (khác A), trong đó \(B \in \left( O \right)\) và \(C \in \left( {O'} \right)\). Tiếp tuyến của (O) tại A cắt BC tại M. Chứng minh rằng:

a) Đường thẳng MA tiếp xúc với (O’);

b) Điểm M là trung điểm của đoạn thẳng BC từ đó suy ra ABC là tam giác vuông.

Phương pháp giải - Xem chi tiết

a) + Chứng minh \(A \in OO'\).

+ Chứng minh \(MA \bot AO\) suy ra \(MA \bot AO'\). Do đó, MA là tiếp tuyến của (O’).

b) + Chứng minh \(MA = MB\), \(MA = MC\) nên \(MA = MB = MC\).

+ Do đó, M là trung điểm của BC.

+ Tam giác ABC có đường trung tuyến AM bằng \(\frac{1}{2}\)BC nên là tam giác vuông tại A.

Lời giải chi tiết

(H.5.41)

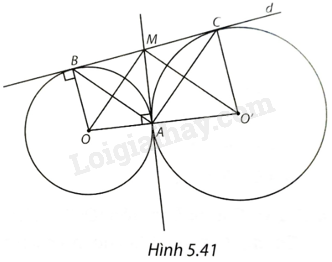
a) Hai đường tròn (O) và (O’) tiếp xúc ngoài tại A nên \(A \in OO'\).

Vì MA là tiếp tuyến của (O) tại A nên \(MA \bot AO\) tại A, từ đó suy ra \(MA \bot AO'\).

Do đó, MA là tiếp tuyến của (O’).

b) MA và MB là hai tiếp tuyến của (O) cắt nhau tai M nên \(MA = MB\).

Tương tự đối với đường tròn (O’), ta cũng có \(MA = MC\).

Do đó, \(MA = MB = MC\). Do đó, \(MB = MC\).

Vậy M là trung điểm của BC.

Tam giác ABC có đường trung tuyến AM bằng \(\frac{1}{2}\)BC nên là tam giác vuông tại A.

Bình luận

Chia sẻ

Bình chọn:

4.9 trên 7 phiếu

Bài tiếp theo

Giải bài 3 trang 120, 121 vở thực hành Toán 9
Cho đường tròn (O) đường kính AB, tiếp tuyến xx’ tại A và tiếp tuyến yy’ tại B của (O). Một tiếp tuyến thứ ba của (O) tại điểm P (P khác A và B) cắt xx’ tại M và cắt yy’ tại N. a) Chứng minh rằng (MN = MA + NB). b) Đường thẳng đi qua O và vuông góc với AB cắt MN tại Q. Chứng minh rằng Q là trung điểm của đoạn MN. c) Chứng minh rằng AB tiếp xúc với đường tròn đường kính MN.
Giải bài 2 trang 119, 120 vở thực hành Toán 9
Khi chuyển động, giả sử đầu mũi kim dài của một chiếc đồng hồ vạch nên một đường tròn, kí hiệu là (T1), trong khi đầu mũi kim ngắn vạch nên một đường tròn khác, kí hiệu là (T2). a) Hai đường tròn (T1) và (T2) có vị trí tương đối như thế nào? b) Giả sử bán kính của (T1) và (T2) lần lượt là ({R_1}) và ({R_2}). Người ta vẽ trên mặt đồng hồ một họa tiết hình tròn có tâm nằm cách điểm trục kim đồng hồ một khoảng bằng (frac{1}{2}{R_1}) và có bán kính bằng (frac{1}{2}{R_2}). Hãy cho biết vị
Giải bài 1 trang 119 vở thực hành Toán 9
Cho hai đường thẳng a và b song song với nhau, điểm O nằm trong phần mặt phẳng ở giữa hai đường thẳng đó. Biết rằng khoảng cách từ O đến a và b lần lượt bằng 2cm và 3cm. a) Hỏi bán kính R của đường tròn (O; R) phải thỏa mãn điều kiện gì để (O; R) cắt cả hai đường thẳng a và b? b) Biết rằng đường tròn (O; R) tiếp xúc với đường thẳng a. Hãy xác định vị trí tương đối của đường tròn (O; R) và đường thẳng b.