Bài 6. Hình thoi - Toán 8 - Cùng khám phá

Giải bài 3.29 trang 80 SGK Toán 8 - Cùng khám phá

Cho hình chữ nhật

Gửi góp ý cho Loigiaihay.com và nhận về những phần quà hấp dẫn

Đề bài

Cho hình chữ nhật \(ABCD\) và \(M,N,P,Q\) lần lượt là trung điểm các cạnh \(AB,BC,CD,AD\). Chứng minh rằng \(MNPQ\) là hình thoi.

Phương pháp giải - Xem chi tiết

Dựa vào tính chất hình chữ nhật và hình thoi để chứng minh

Lời giải chi tiết

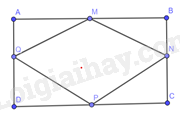
Xét tam giác \(MBN\) và \(NCP\), ta có:

\(BN = NC\) (N là trung điểm)

\(\widehat {MBN} = \widehat {NCP} = 90^\circ \) (do \(ABCD\) là hình chữ nhật)

\(MB = CP\) (do \(M\) và \(P\) lần lượt là trung điểm của \(AB\) và \(CD\))

→ \(\Delta MBN = \Delta NCP\)

→ \(\Delta MBN = \Delta AMQ = \Delta NCP = \Delta QDP\)

→ \(MQ = MN = NP = QP\) (các cạnh tương ứng)

→ Tứ giác \(MNPQ\) là hình thoi

Bình luận

Chia sẻ

Bình chọn:

4.9 trên 7 phiếu

>> Xem thêm

Báo lỗi - Góp ý

Các bài khác cùng chuyên mục

TẢI APP ĐỂ XEM OFFLINE