Giải bài 3 trang 58 vở thực hành Toán 8

Cho tam giác ABC, đường cao AH. Gọi M là trung điểm của AC, N là điểm sao cho M là trung điểm của HN. Chứng minh tứ giác AHCN là hình chữ nhật.

Đề bài

Cho tam giác ABC, đường cao AH. Gọi M là trung điểm của AC, N là điểm sao cho M là trung điểm của HN. Chứng minh tứ giác AHCN là hình chữ nhật.

Phương pháp giải - Xem chi tiết

Dựa vào dấu hiệu nhận biết hình chữ nhật.

Lời giải chi tiết

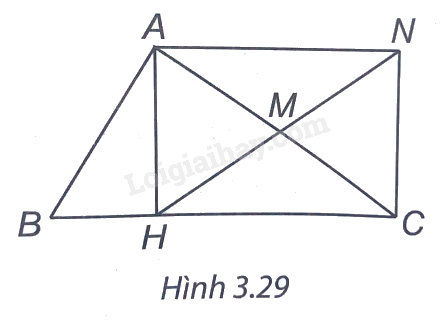
(H.3.29). Ta có: AM = MC, HM = MN nên tứ giác AHCN có hai đường chéo AC, HN cắt nhau tại trung điểm mỗi đường nên AHCN là hình bình hành.

Vì \(\widehat {AHC} = 90^\circ \) hay hình bình hành AHCN có một góc vuông nên AHCN là hình chữ nhật.

Bình luận

Chia sẻ

Bình chọn:

4.9 trên 7 phiếu

Bài tiếp theo

Giải bài 4 trang 58 vở thực hành Toán 8
Xét một điểm M trên cạnh huyền của tam giác ABC vuông cân tại A. Gọi N và P lần lượt là hình chiếu vuông góc của M trên các cạnh AB và AC.
Giải bài 5 trang 58 vở thực hành Toán 8
Cho hình chữ nhật ABCD. Gọi O là trung điểm của AC. Hạ OM vuông góc với BC tại M, ON vuông góc với BC tại N.
Giải bài 2 trang 58 vở thực hành Toán 8
Bằng compa, nêu cách kiểm tra một tứ giác có là hình chữ nhật hay không. Giải thích kết quả.
Giải bài 1 trang 57 vở thực hành Toán 8
Bằng ê ke, nêu cách kiểm tra một tứ giác có là hình chữ nhật hay không. Hãy giải thích kết quả.
Giải câu hỏi trắc nghiệm trang 57, 58 vở thực hành Toán 8
Chọn phương án đúng trong mỗi câu sau:

>> Xem thêm

Luyện Bài Tập Trắc nghiệm Toán 8 - Kết nối tri thức - Xem ngay

Báo lỗi - Góp ý

Tham Gia Group Dành Cho 2K10 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí

>> Học trực tuyến lớp 9 & lộ trình Up 10! trên Tuyensinh247.com Đầy đủ khoá học các bộ sách (Kết nối tri thức với cuộc sống; Chân trời sáng tạo; Cánh diều), theo lộ trình 3 bước: Nền Tảng, Luyện Thi, Luyện Đề. Bứt phá điểm lớp 9, thi vào lớp 10 kết quả cao. Hoàn trả học phí nếu học không hiệu quả.