-
Toán 8 tập 1 - Cánh diều
-
Toán 8 tập 2 - Cánh diều
-
Chương 6 Một số yếu tố thống kê và xác suất
- Bài 1. Thu thập và phân loại dữ liệu
- Bài 2. Mô tả và biểu diễn dữ liệu trên các bảng, biểu đồ
- Bài 3. Phân tích và xử lí dữ liệu thu được ở dạng bảng, biểu đồ
- Bài 4. Xác suất của biến cố ngẫu nhiên trong một số trò chơi đơn giản
- Bài 5. Xác suất thực nghiệm của một biến cố trong một số trò chơi đơn giản
- Bài tập cuối chương 6
-
Chương 7 Phương trình bậc nhất một ẩn
-
Chương 8 Tam giác đồng dạng. Hình đồng dạng
- Bài 1. Định lí Thalès trong tam giác
- Bài 2. Ứng dụng của định lí Thalès trong tam giác
- Bài 3. Đường trung bình của tam giác
- Bài 4. Tính chất đường phân giác của tam giác
- Bài 5. Tam giác đồng dạng
- Bài 6. Trường hợp đồng dạng thứ nhất của tam giác
- Bài 7. Trường hợp đồng dạng thứ hai của tam giác
- Bài 8. Trường hợp đồng dạng thứ ba của tam giác
- Bài 9. Hình đồng dạng
- Bài 10. Hình đồng dạng trong thực tiễn
- Bài tập cuối chương 8
-
Giải bài 3 trang 111 SGK Toán 8 tập 1 - Cánh diều
Cho hình chữ nhật ABCD
Tổng hợp đề thi học kì 2 lớp 8 tất cả các môn - Cánh diều
Toán - Văn - Anh - Khoa học tự nhiên
Đề bài
Cho hình chữ nhật ABCD có điểm E nằm trên cạnh CD sao cho \(\widehat {A{\rm{E}}B} = {78^o};\widehat {EBC} = {39^o}\). Tính số đo của \(\widehat {BEC}\) và \(\widehat {E{\rm{A}}B}\).
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
Vận dụng định lí: tổng các trong của một tứ giác bằng 360 độ
Lời giải chi tiết
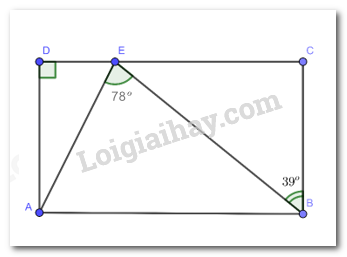
Xét tam giác BEC vuông tại C có:
\(\begin{array}{l}\widehat {BEC} + \widehat {EBC} + \widehat {BCE} = {180^o}\\ \Rightarrow \widehat {BEC} + {39^o} + {30^o} = {180^o}\\ \Rightarrow \widehat {BEC} = {180^o} - {39^o} - {30^o} = {51^o}\end{array}\)
Mà: \(\begin{array}{l}\widehat {EBA} + \widehat {EBC} = {90^o}\\ \Rightarrow \widehat {EBA} = {90^o} - \widehat {EBC} = {90^o} - {39^o} = {51^o}\end{array}\)
Xét tam giác AEB có:
\(\begin{array}{l}\widehat {A{\rm{E}}B} + \widehat {E{\rm{A}}B} + \widehat {EBA} = {180^o}\\ \Rightarrow \widehat {E{\rm{A}}B} = {180^o} - \widehat {A{\rm{E}}B} - \widehat {EBA} = {180^o} - {78^o} - {51^o} = {51^o}\end{array}\)
Bình luận
Chia sẻ
- Giải bài 4 trang 111 SGK Toán 8 tập 1 - Cánh diều
- Giải bài 5 trang 111 SGK Toán 8 tập 1 - Cánh diều
- Giải bài 2 trang 111 SGK Toán 8 tập 1 - Cánh diều
- Giải bài 1 trang 111 SGK Toán 8 tập 1 - Cánh diều
- Giải mục 3 trang 110,111 SGK Toán 8 tập 1 - Cánh diều
>> Xem thêm
Luyện Bài Tập Trắc nghiệm Toán 8 - Cánh diều - Xem ngay
Tham Gia Group Dành Cho 2K10 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí
>> Học trực tuyến lớp 9 & lộ trình Up 10! trên Tuyensinh247.com Đầy đủ khoá học các bộ sách (Kết nối tri thức với cuộc sống; Chân trời sáng tạo; Cánh diều), theo lộ trình 3 bước: Nền Tảng, Luyện Thi, Luyện Đề. Bứt phá điểm lớp 9, thi vào lớp 10 kết quả cao. Hoàn trả học phí nếu học không hiệu quả.
 |
 |
 |
 |
 |
 |
Các bài khác cùng chuyên mục
