Bài 22 trang 102 SBT toán 9 tập 2

Giải bài 22 trang 102 sách bài tập toán 9.Vẽ một tam giác vuông biết cạnh huyền là 4cm và đường cao ứng với cạnh huyền là 1,5cm.

Đề bài

Vẽ một tam giác vuông biết cạnh huyền là $4cm$ và đường cao ứng với cạnh huyền là $1,5cm.$

Phương pháp giải - Xem chi tiết

Ta sử dụng kiến thức:

+) Góc nội tiếp chắn nửa đường tròn là góc vuông.

Lời giải chi tiết

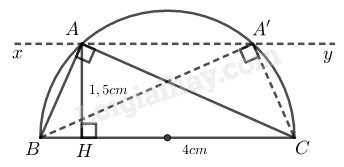
Cách vẽ:

- Vẽ đoạn $BC = 4cm.$

- Vẽ nửa đường tròn đường kính $BC$

- Vẽ đường thẳng $xy$ nằm trên nửa mặt phẳng chứa nửa đường tròn và $xy // BC,$ cách $BC$ một khoảng bằng $1,5cm.$

- Đường thẳng $xy$ cắt nửa đường tròn đường kính $BC$ tại $A$ và $A’.$ Nối $AB, AC, A’B, A’C$ ta có $∆ABC$ hoặc $∆A'BC$ cần vẽ.

Chứng minh:

Vì $xy$ cách $BC$ một khoảng $1,5m < \displaystyle {{BC} \over 2} = 2cm$ nên đường thẳng $xy$ cắt nửa đường tròn đường kính $BC.$

Ta lại có $∆ABC$ nội tiếp trong nửa đường tròn đường kính $BC$ nên $\widehat {BAC} = {90^o}$

Có $AH \bot BC$ và $AH = 1,5 cm.$

Vậy tam giác $ABC$ hoặc tam giác $A'BC$ thỏa mãn đề bài.

Loigiaihay.com

Bình luận

Chia sẻ

Bình chọn:

3.9 trên 9 phiếu

Bài tiếp theo

Bài 23 trang 103 SBT toán 9 tập 2
Giải bài 23 trang 103 sách bài tập toán 9. Cho tam giác cân ABC (AB = AC) nội tiếp đường tròn tâm O...
Bài 3.1 phần bài tập bổ sung trang 103 SBT toán 9 tập 2
Giải bài 3.1 phần bài tập bổ sung trang 103 SBT toán 9.Mỗi câu sau đây đúng hay sai...
Bài 3.2 phần bài tập bổ sung trang 103 SBT toán 9 tập 2
Giải bài 3.2 phần bài tập bổ sung trang 103 sách bài tập toán 9.Cho nửa đường tròn đường kính AB, tâm O. Đường tròn tâm A bán kính AO cắt nửa đường tròn đã cho tại C...
Bài 21 trang 102 SBT toán 9 tập 2
Giải bài 21 trang 102 sách bài tập toán 9. Cho tam giác ABC nội tiếp trong đường tròn tâm O,...
Bài 20 trang 102 SBT toán 9 tập 2
Giải bài 20 trang 102 sách bài tập toán 9.Cho tam giác đều ABC nội tiếp đường tròn (O) và M là một điểm của cung nhỏ BC. Trên MA lấy điểm D sao cho MD = MB...
Bài 19 trang 102 SBT toán 9 tập 2
Giải bài 19 trang 102 sách bài tập toán 9. Để giúp xe lửa chuyển từ một đường ray từ hướng này sang một đường ray theo hướng khác, người ta làm xen giữa một đoạn đường ray hình vòng cung...
Bài 18 trang 102 SBT toán 9 tập 2
Giải bài 18 trang 102 sách bài tập toán 9. Cho đường tròn (O) và một điểm M cố định không nằm trên đường tròn. Qua M vẽ một cát tuyến bất kì cắt đường tròn ở A và B. Chứng minh rằng tích MA.MB không đổi.
Bài 17 trang 102 SBT toán 9 tập 2
Giải bài 17 trang 102 sách bài tập toán 9. Cho đường tròn (O) và hai dây AB, AC bằng nhau. Qua A vẽ một cát tuyến cắt dây BC ở D và cắt đường tròn (O) ở E...
Bài 16 trang 102 SBT toán 9 tập 2
Giải bài 16 trang 102 sách bài tập toán 9. Cho đường tròn (O) và hai đường kính AB, CD vuông góc với nhau. Lấy một điểm M trên cung AC rồi vẽ tiếp tuyến với đường tròn (O) tại M...
Bài 15 trang 102 SBT toán 9 tập 2
Giải bài 15 trang 102 sách bài tập toán 9. Cho đường tròn tâm O, bán kính 1,5cm. Hãy vẽ hình vuông ABCD có bốn đỉnh nằm trên đường tròn đó. Nêu cách vẽ.