Giải bài 2 trang 121 sách bài tập toán 11 - Chân trời sáng tạo tập 1

Cho hai hình bình hành ABCD và ABEF không cùng nằm trong một mặt phẳng có tâm lần lượt là O và O’. a) Chứng minh OO’ song song với các mặt phẳng (ADF) và (BCE). b) Gọi M, N lần lượt là hai điểm thuộc hai cạnh AF, AD sao cho \(AM = \frac{1}{3}AF,\) \(AN = \frac{1}{3}AD\). Chứng minh MN//(DCEF).

Tổng hợp đề thi giữa kì 1 lớp 11 tất cả các môn - Chân trời sáng tạo

Toán - Văn - Anh - Lí - Hóa - Sinh

Đề bài

Cho hai hình bình hành ABCD và ABEF không cùng nằm trong một mặt phẳng có tâm lần lượt là O và O’.

a) Chứng minh OO’ song song với các mặt phẳng (ADF) và (BCE).

b) Gọi M, N lần lượt là hai điểm thuộc hai cạnh AF, AD sao cho \(AM = \frac{1}{3}AF,\) \(AN = \frac{1}{3}AD\). Chứng minh MN//(DCEF).

Phương pháp giải - Xem chi tiết

Sử dụng kiến thức về điều kiện để một đường thẳng song song với một mặt phẳng để chứng minh: Nếu đường thẳng a không nằm trong mặt phẳng (P) và song song với một đường thẳng b nào đó nằm trong (P) thì a song song với (P).

Lời giải chi tiết

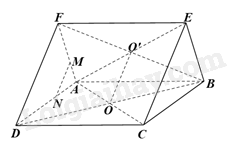
a) Vì O, O’ lần lượt là tâm của hình bình hành ABCD và ABEF nên O là trung điểm của BD, AC và O’ là trung điểm của BF, AE.

Vì O là trung điểm của BD, O’ là trung điểm của BF nên OO’ là đường trung bình của tam giác BDF. Do đó, OO’//DF (1)

Vì O là trung điểm của AC, O’ là trung điểm của AE nên OO’ là đường trung bình của tam giác ACE. Do đó, OO’//CE (2)

Từ (1) và (2) ta có: OO’//DF//CE

Vì OO’//DF, OO’ không nằm trên mặt phẳng (ADF) và \(DF \subset \left( {ADF} \right)\) nên OO’//(ADF).

Vì OO’//CE, OO’ không nằm trên mặt phẳng (BCE) và \(CE \subset \left( {BCE} \right)\) nên OO’//(BCE).

b) Vì \(AM = \frac{1}{3}AF,AN = \frac{1}{3}AD \Rightarrow \frac{{AM}}{{AF}} = \frac{{AN}}{{AD}} = \frac{1}{3}\)

Tam giác ADF có: \(\frac{{AM}}{{AF}} = \frac{{AN}}{{AD}} = \frac{1}{3}\) nên MN//DF (định lí Thalès đảo)

Vì MN//DF, MN không nằm trên mặt phẳng (DCEF) và \(DF \subset \left( {DCEF} \right)\) nên MN//(DCEF).

Bình luận

Chia sẻ

Bình chọn:

4.9 trên 7 phiếu

Bài tiếp theo

Giải bài 3 trang 122 sách bài tập toán 11 - Chân trời sáng tạo tập 1
Cho hình chóp S. ABCD có đáy ABCD là một hình bình hành. Gọi G là trọng tâm của tam giác SAB, I là trung điểm của AB và M là điểm thuộc cạnh AD sao cho \(AM = \frac{1}{3}AD\). Đường thẳng đi qua M và song song với AB cắt CI tại N. Chứng minh: a) NG//(SCD); b) MG//(SCD).
Giải bài 4 trang 122 sách bài tập toán 11 - Chân trời sáng tạo tập 1
Cho hình chóp S. ABCD có đáy ABCD là hình bình hành. Gọi M, N lần lượt là trung điểm của hai cạnh AB và CD, P là trung điểm của SA. Chứng minh: a) MN song song với các mặt phẳng (SBC) và (SAD); b) SB song song với (MNP); c) SC song song với (MNP); d) Gọi \({G_1}\) và \({G_2}\) theo thứ tự là trọng tâm của hai tam giác ABC và SBC. Chứng minh \({G_1}{G_2}\) song song với (SAD).
Giải bài 5 trang 122 sách bài tập toán 11 - Chân trời sáng tạo tập 1
Cho hình chóp S. ABCD có đáy là hình bình hành. Gọi \(\left( \alpha \right)\) là mặt phẳng đi qua trung điểm M của cạnh AB, song song với BD và SA. Tìm giao tuyến của mặt phẳng \(\left( \alpha \right)\) với các mặt của hình chóp.
Giải bài 1 trang 121 sách bài tập toán 11 - Chân trời sáng tạo tập 1
Cho tứ diện ABCD. Gọi \({G_1}\) và \({G_2}\) lần lượt là trọng tâm của hai tam giác ABD và ACD. Chứng minh \({G_1}{G_2}\) song song với các mặt phẳng (ABC) và (BCD).