Giải bài 2 trang 108 vở thực hành Toán 9

Cho tam giác ABC không là tam giác vuông. Gọi H và K là chân các đường vuông góc lần lượt hạ từ B và C xuống AC và AB. Chứng minh rằng: a) Đường tròn đường kính BC đi qua các điểm H và K; b) (KH < BC).

Tổng hợp đề thi học kì 1 lớp 9 tất cả các môn - Kết nối tri thức

Toán - Văn - Anh - KHTN - Lịch sử và Địa lí

Đề bài

Cho tam giác ABC không là tam giác vuông. Gọi H và K là chân các đường vuông góc lần lượt hạ từ B và C xuống AC và AB. Chứng minh rằng:

a) Đường tròn đường kính BC đi qua các điểm H và K;

b) \(KH < BC\).

Phương pháp giải - Xem chi tiết

a) Gọi O là trung điểm của BC. Chứng minh \(OH = OK = \frac{1}{2}BC\) nên đường tròn đường kính BC đi qua các điểm H và K.

b) Trong một đường tròn, đường kính là dây cung lớn nhất.

Lời giải chi tiết

(H.5.20)

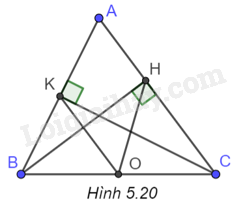
a) Gọi O là trung điểm của BC. Do \(\widehat {BHC} = \widehat {BKC} = {90^o}\) nên các tam giác BKC, BHC lần lượt vuông tại K và H.

Ta có: \(OH = OK = \frac{1}{2}BC\). Do đó, đường tròn đường kính BC đi qua các điểm H và K.

b) Theo câu a, HK là dây của đường tròn đường kính BC. Do đó, \(KH < BC\).

Bình luận

Chia sẻ

Bình chọn:

3.6 trên 5 phiếu

Bài tiếp theo

Giải bài 3 trang 108 vở thực hành Toán 9
Có thể xem guồng nước (còn gọi là cọn nước) là một công cụ hay cỗ máy có dạng hình tròn, quay được nhờ sức nước chảy (H.5.21a). Guồng nước thường thấy ở các vùng miền núi. Nhiều guồng nước được làm bằng tre, dùng để đưa nước lên ruộng cao, giã gạo hoặc làm một số việc khác. Giả sử ngấn nước ngăn cách giữa phần trên và phần dưới của một guồng nước được biểu thị bởi cung ứng với một dây dài 4 m và điểm ngập sâu nhất là 0,5 m (trên Hình 5.21b, điểm ngập sâu nhất là điểm C, ta có AB = 4 m và HC = 0
Giải bài 4 trang 109 vở thực hành Toán 9
Cho đường tròn (O; 5cm). a) Hãy nêu cách vẽ dây AB sao cho khoảng cách từ điểm O đến dây AB bằng 2,5cm. b) Tính độ dài của dây AB trong câu a (làm tròn đến hàng phần trăm). c) Tính số đo và độ dài của cung nhỏ AB. d) Tính diện tích hình quạt tròn ứng với cung nhỏ AB.
Giải bài 5 trang 109, 110 vở thực hành Toán 9
Ba bộ phận truyền chuyển động của một chiếc xe đạp gồm một giò đĩa (bánh răng gắn với bàn đạp), một chiếc líp (cũng có dạng bánh răng) gắn với bánh xe và bộ xích (H.5.23). Biết rằng giò đĩa có bán kính 15 cm, líp có bán kính 4 cm và bánh xe có đường kính 65 cm. Hỏi khi người đi xe đạp một vòng thì xe chạy được quãng đường dài bao nhiêu mét (làm tròn kết quả đến hàng phần chục)?
Giải bài 6 trang 110, 111 vở thực hành Toán 9
Cho tam giác đều ABC có (AB = 2sqrt 3 cm). Nửa đường tròn đường kính BC cắt hai cạnh AB và AC lần lượt tại D và E (khác B và C). (H.5.24). a) Chứng tỏ rằng ba cung nhỏ BD, DE và EC bằng nhau. Tính số đo mỗi cung ấy. b) Tính diện tích của hình viên phân giới hạn bởi dây BD và cung nhỏ BD.
Giải bài 7 trang 111 vở thực hành Toán 9
Cho đường tròn (O), đường kính (AB = 4sqrt 3 cm). Điểm C thuộc đường tròn tâm O sao cho (widehat {AOC} = {60^o}). Tính diện tích hình viên phân giới hạn bởi dây AC và cung nhỏ AC.
Giải bài 1 trang 107 vở thực hành Toán 9
Cho dây AB không đi qua tâm của đường tròn (O). Gọi A’ và B’ là hai điểm lần lượt đối xứng với A và B qua O. Hỏi đường trung trực của A’B’ có phải là trục đối xứng của (O) hay không? Tại sao?