Giải bài 16 trang 90 sách bài tập toán 9 - Cánh diều tập 2

Cho đường tròn (O) ngoại tiếp tam giác đều ABC. Điểm E nằm trên cung nhỏ BC (E khác B và C). ED là tia đối của tia EB. Chứng minh EC là phân giác của góc AED và EA là phân giác của góc BEC.

Đề bài

Cho đường tròn (O) ngoại tiếp tam giác đều ABC. Điểm E nằm trên cung nhỏ BC (E khác B và C). ED là tia đối của tia EB. Chứng minh EC là phân giác của góc AED và EA là phân giác của góc BEC.

Phương pháp giải - Xem chi tiết

Chứng minh \(\widehat {AEB} = \widehat {AEC} = {60^o}\)suy ra EA là phân giác của góc BEC.

Lời giải chi tiết

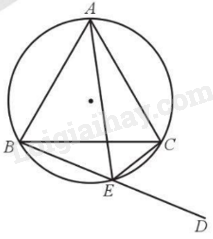
Ta có tứ giác ABEC nội tiếp đường tròn nên \(\widehat {CED} = \widehat {BAC} = {60^o}( = {180^o} - \widehat {BEC})\). Mặt khác \(\widehat {AEC} = \widehat {CED} = {60^o}\). Do đó, EC là phân giác của góc AED.

Tương tự ta có \(\widehat {AEC} = \widehat {ABC} = {60^o}\) và \(\widehat {AEB} = \widehat {ACB} = {60^o}\).

Do đó \(\widehat {AEB} = \widehat {AEC} = {60^o}\) hay EA là phân giác của góc BEC.

Bình luận

Chia sẻ

Bình chọn:

4.9 trên 7 phiếu

Bài tiếp theo

Giải bài 17 trang 90 sách bài tập toán 9 - Cánh diều tập 2
Cho tam giác ABC cân ở A, H là trung điểm của BC và (widehat {BAC} < {90^o}). Đường vuông góc với AB tại A cắt đường thẳng BC ở D. Kẻ DE vuông góc với AC. Chứng minh: a) AH = EH b) (widehat {DCE} = widehat {ABD}).
Giải bài 18 trang 91 sách bài tập toán 9 - Cánh diều tập 2
Cho (widehat {xAy} = {60^o}) và điểm B nằm trong góc xAy. Kẻ đường thẳng BN vuông góc với Ay cắt Ax tại H; kẻ đường thẳng BM vuông góc với Ax cắt Ay tại K (Hình 14). Chứng minh: a) Các tứ giác AMBN, HMNK là các tứ giác nội tiếp đường tròn. b) HK = 2MN
Giải bài 19 trang 91 sách bài tập toán 9 - Cánh diều tập 2
Cho hình vuông ABCD. Trên cạnh AB lấy điểm M. Đường thẳng qua C vuông góc với CM cắt các tia AB, AD lần lượt tại E và F. Tia CM cắt đường thẳng AD tại N. Chứng minh rằng: a) (widehat {NCA} = widehat {MFN}) và (widehat {NEA} = widehat {NCA}) b) CM + CN = EF.
Giải bài 20 trang 91 sách bài tập toán 9 - Cánh diều tập 2
Chứng minh rằng mỗi hình thang cân là một tứ giác nội tiếp đường tròn.
Giải bài 21 trang 91 sách bài tập toán 9 - Cánh diều tập 2
Hình vuông ABCD có cạnh bằng 1, người ta nối trung điểm các cạnh liên tiếp của nó để tạo thành tứ giác EFGH, tiếp tục như vậy được tứ giác mới IKPQ (Hình 15). Chứng minh: a) Tứ giác EFGH và tứ giác IKPQ là các tứ giác nội tiếp đường tròn. b) Tỉ số bán kính đường tròn ngoại tiếp hình vuông ABCD và bán kính của đường tròn ngoại tiếp tứ giác EFGH bằng tỉ số bán kính đường tròn ngoại tiếp tứ giác EFGH và bán kính đường tròn ngoại tiếp tứ giác IKPQ.
Giải bài 22 trang 91 sách bài tập toán 9 - Cánh diều tập 2
Cho tam giác ABC vuông cân tại C và nội tiếp đường tròn (O;R). E là điểm tùy ý trên cung nhỏ AC. Gọi I là giao điểm của EB và AC. Kẻ IK vuông góc với AB. Chứng minh rằng khi E di chuyển trên cung nhỏ AC thì EK luôn đi qua một điểm cố định.
Giải bài 15 trang 90 sách bài tập toán 9 - Cánh diều tập 2
Ở Hình 13, hai đường tròn (O), (O’) giao nhau tại A, B và CD là một dây cung của (O). Tia CA cắt (O’) tại E và tia DB cắt (O’) tại F. Chứng minh EF song song với CD.
Giải bài 14 trang 90 sách bài tập toán 9 - Cánh diều tập 2
Chứng minh rằng trong một đường tròn, hai dây không đi qua tâm không thể cắt nhau tại trung điểm mỗi đường.
Giải bài 13 trang 90 sách bài tập toán 9 - Cánh diều tập 2
Cho tứ giác ABCD nội tiếp đường tròn. Tính số đo mỗi góc còn lại của tứ giác đó trong mỗi trường hợp sau: a) (widehat A = 3widehat C) và (widehat B = 5widehat D); b) (widehat A - widehat C = {12^o}) và (widehat D - widehat B = {76^o}) c) (widehat A = 7widehat B) và (widehat A + 2widehat B = {180^o}) d) (widehat D - widehat C = {20^o}) và (widehat D + widehat C = {100^o})
Giải bài 12 trang 90 sách bài tập toán 9 - Cánh diều tập 2
Tìm phát biểu sai trong các phát biểu sau: a) Tứ giác có bốn đỉnh thuộc một đường tròn được gọi là tứ giác nội tiếp đường tròn. b) Trong một tứ giác nội tiếp đường tròn, tổng số đo hai góc bất kì bằng 180o. c) Hình chữ nhật luôn nội tiếp đường tròn. d) Mỗi hình vuông là tứ giác nội tiếp đường tròn