Giải bài 12 trang 77 sách bài tập toán 11 - Chân trời sáng tạo tập 1
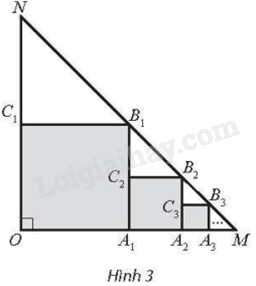
Cho tam giác OMN vuông cân tại O, \(OM = ON = 1\). Trong tam giác OMN, vẽ hình vuông \(O{A_1}{B_1}{C_1}\) sao cho các đỉnh \({A_1},{B_1},{C_1}\) lần lượt nằm trên các cạnh OM, MN, ON. Trong tam giác \({A_1}M{B_1}\), vẽ hình vuông \({A_1}{A_2}{B_2}{C_2}\) sao cho các đỉnh \({A_2},{B_2},{C_2}\) lần lượt nằm trên các cạnh \({A_1}M,M{B_1},{A_1}{B_1}\). Tiếp tục quá trình đó, ta được một dãy các hình vuông (Hình 3). Tính tổng diện tích các hình vuông này.
Đề bài
Cho tam giác OMN vuông cân tại O, \(OM = ON = 1\). Trong tam giác OMN, vẽ hình vuông \(O{A_1}{B_1}{C_1}\) sao cho các đỉnh \({A_1},{B_1},{C_1}\) lần lượt nằm trên các cạnh OM, MN, ON. Trong tam giác \({A_1}M{B_1}\), vẽ hình vuông \({A_1}{A_2}{B_2}{C_2}\) sao cho các đỉnh \({A_2},{B_2},{C_2}\) lần lượt nằm trên các cạnh \({A_1}M,M{B_1},{A_1}{B_1}\). Tiếp tục quá trình đó, ta được một dãy các hình vuông (Hình 3). Tính tổng diện tích các hình vuông này.
Phương pháp giải - Xem chi tiết
Sử dụng kiến thức về tổng của cấp số nhân lùi vô hạn để tính tổng: Cấp số nhân vô hạn \(\left( {{u_n}} \right)\) có công bội q thỏa mãn \(\left| q \right| < 1\) được gọi là cấp số nhân lùi vô hạn. Cấp số nhân lùi vô hạn này có tổng là: \(S = {u_1} + {u_2} + ... + {u_n} + ... = \frac{{{u_1}}}{{1 - q}}\)
Lời giải chi tiết
Độ dài cạnh của các hình vuông lần lượt là:
\({a_1} = \frac{1}{2},{a_2} = \frac{1}{2}{a_1} = \frac{1}{2}.\frac{1}{2} = {\left( {\frac{1}{2}} \right)^2},{a_3} = \frac{1}{2}{a_2} = \frac{1}{2}{\left( {\frac{1}{2}} \right)^2} = {\left( {\frac{1}{2}} \right)^3},...\)
Diện tích của các hình vuông lần lượt là:
\({S_1} = a_1^2 = {\left( {\frac{1}{2}} \right)^2} = \frac{1}{4},\)
\({S_2} = a_2^2 = {\left( {{{\left( {\frac{1}{2}} \right)}^2}} \right)^2} = {\left( {\frac{1}{4}} \right)^2},\)
\({S_3} = a_3^2 = {\left( {{{\left( {\frac{1}{2}} \right)}^3}} \right)^2} = {\left( {\frac{1}{4}} \right)^3},...\)
Các diện tích \({S_1},{S_2},{S_3},...\) lập thành một cấp số nhân lùi vô hạn với số hạng đầu là \({S_1} = \frac{1}{4}\) và công bội bằng \(\frac{1}{4}\).
Do đó, tổng diện tích các hình vuông là: \(S = \frac{1}{4}.\frac{1}{{1 - \frac{1}{4}}} = \frac{1}{3}\)
- Giải bài 13 trang 77 sách bài tập toán 11 - Chân trời sáng tạo tập 1
- Giải bài 11 trang 76 sách bài tập toán 11 - Chân trời sáng tạo tập 1
- Giải bài 10 trang 76 sách bài tập toán 11 - Chân trời sáng tạo tập 1
- Giải bài 9 trang 76 sách bài tập toán 11 - Chân trời sáng tạo tập 1
- Giải bài 8 trang 76 sách bài tập toán 11 - Chân trời sáng tạo tập 1
>> Xem thêm
Luyện Bài Tập Trắc nghiệm Toán 11 - Chân trời sáng tạo - Xem ngay
Các bài khác cùng chuyên mục
- Giải bài 5 trang 162 sách bài tập toán 11 - Chân trời sáng tạo tập 1
- Giải bài 4 trang 161 sách bài tập toán 11 - Chân trời sáng tạo tập 1
- Giải bài 3 trang 161 sách bài tập toán 11 - Chân trời sáng tạo tập 1
- Giải bài 2 trang 161 sách bài tập toán 11 - Chân trời sáng tạo tập 1
- Giải bài 1 trang 161 sách bài tập toán 11 - Chân trời sáng tạo tập 1
- Giải bài 5 trang 162 sách bài tập toán 11 - Chân trời sáng tạo tập 1
- Giải bài 4 trang 161 sách bài tập toán 11 - Chân trời sáng tạo tập 1
- Giải bài 3 trang 161 sách bài tập toán 11 - Chân trời sáng tạo tập 1
- Giải bài 2 trang 161 sách bài tập toán 11 - Chân trời sáng tạo tập 1
- Giải bài 1 trang 161 sách bài tập toán 11 - Chân trời sáng tạo tập 1













Danh sách bình luận