Đề thi học kì 2 Toán 11 - Đề số 2
Phần I. Câu trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi thí sinh chỉ chọn một phương án.
Đề bài
Cho hàm số \(f(x) = \frac{{{x^3}}}{3} - \frac{3}{2}{x^2} - 4x + 6.\) Phương trình \(f'(x) = 0\) có nghiệm là
-
A.
\(x = - 1\)
-
B.
\(x = 1,\,\,x = 4\)
-
C.
\(x = - 1,\,\,x = 4\)
-
D.
\(x = 0,\,\,x = 3\)
Gọi (d) là tiếp tuyến của đồ thị hàm số\(y = f(x) = - {x^3} + x\) tại điểm \(M( - 2;6).\) Phương trình của (d) là
-
A.
y = -11x +30.
-
B.
y = 13x + 34.
-
C.
y = -11x – 16.
-
D.
y = 13x – 18.
Tính \(\mathop {\lim }\limits_{x \to 3} \frac{{\sqrt {x + 1} - 2}}{{9 - {x^2}}}\) bằng
-
A.
\( - \frac{1}{{24}}\)
-
B.
\( - \frac{1}{6}\)
-
C.
\(\frac{1}{6}\)
-
D.
\(\frac{1}{{24}}\)
Cho \(u = u\left( x \right),v = v\left( x \right),v\left( x \right) \ne 0\); với k là hằng số. Hãy chọn khẳng định sai?
-
A.
\({\left( {\frac{1}{v}} \right)^\prime } = - \frac{{v'}}{{{v^{}}}}\)
-
B.
\(\left( {u + v} \right)' = u' + v'\)
-
C.
\({\left( {k.u} \right)^\prime } = k.u'\)
-
D.
\(\left( {u.v} \right)' = u'.v + u.v'\)
Đạo hàm của hàm số \(y = \frac{{2x - 1}}{{1 - x}}\) là
-
A.
\(y' = \frac{3}{{{{\left( { - x + 1} \right)}^2}}}\)
-
B.
\(y' = \frac{1}{{{{\left( {x - 1} \right)}^2}}}\)
-
C.
\(y' = \frac{{ - 1}}{{{{\left( {1 - x} \right)}^2}}}\)
-
D.
\(y' = \frac{{ - 3}}{{{{\left( {1 - x} \right)}^2}}}\)
Cho hàm số: \(f(x) = \left\{ \begin{array}{l}\frac{{{x^2} - 1}}{{x - 1}}\quad khi\;x \ne 1\\m\quad \quad \quad khi\;x = 1\end{array} \right.\) . Để f(x) liên tục tại điểm \({x_0} = 1\)thì m bằng:
-
A.
-1
-
B.
1
-
C.
2
-
D.
0
Tìm đạo hàm của hàm số sau \(y = {x^4} - 3{x^2} + 2x - 1\)
-
A.
\(y' = 4{x^3} - 3x + 2\)
-
B.
\(y' = 4{x^4} - 6x + 2\)
-
C.
\(y' = 4{x^3} - 6x + 3\)
-
D.
\(y' = 4{x^3} - 6x + 2\)
Cho hàm số \(f(x) = \frac{{a{x^2} + 4x + 3}}{{3x - 2a{x^2}}},(a \in R,a \ne 0)\). Khi đó \(\mathop {\lim }\limits_{x \to - \infty } f(x)\) bằng
-
A.
\( - \frac{1}{2}\)
-
B.
\( + \infty \)
-
C.
\(\frac{a}{3}\)
-
D.
\( - \infty \)
Cho hình chóp \(S.ABC\) có đáy ABC là tam giác vuông tại B và SA vuông góc mặt đáy \(\left( {ABC} \right)\), \(SB = 2a\), \(AB = a\)( tham khảo hình vẽ). Tính góc giữa SB và \(mp\left( {ABC} \right)\)
-
A.
\(90^\circ .\)
-
B.
\(60^\circ .\)
-
C.
\(45^\circ .\)
-
D.
\(30^\circ .\)
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, cạnh bên SA vuông góc với đáy. Khẳng định nào sau đây đúng?
-
A.
\(AC \bot (SBD)\)
-
B.
\((SCD) \bot (SAD)\)
-
C.
\((SBD) \bot (SAC)\)
-
D.
\((SBC) \bot (SAC)\)
Cho hình chóp S.ABCD có đáy ABCD là hình thoi tâm O và SA = SC, SB = SD. Khẳng định nào sau đây đúng ?
-
A.
\(AC \bot (SBD)\)
-
B.
\(AB \bot (SAD)\)
-
C.
\(AC \bot (SBD)\)
-
D.
\(SO \bot (ABCD)\)
Với hàm số \(g\left( x \right) = \frac{{\left( {2x + 1} \right){{\left( {2 - 3x} \right)}^2}}}{{x - 1}};\,g'\left( 2 \right)\) bằng
-
A.
232.
-
B.
72.
-
C.
152.
-
D.
-75.
Trong một chiếc hộp có 20 viên bi, trong đó có 8 viên bi màu đỏ, 7 viên bi màu xanh và 5 viên bi màu vàng. Lấy ngẫu nhiên ra 3 viên bi
a) Xác suất để 3 viên bi lấy ra đều màu đỏ là \(\frac{{14}}{{285}}\)
b) Xác suất để 3 viên bi lấy ra có không quá hai màu là \(\frac{{43}}{{57}}\)
c) Xác suất để 3 viên bi lấy ra đều có màu vàng là \(\frac{1}{7}\)
d) Xác suất để 3 viên bi lấy ra có đủ cả ba màu là \(\frac{{14}}{{57}}\)
Cho hàm số có đồ thị (C): \(y = f(x) = \frac{{x - 2}}{{x - 1}}\)
a) Phương trình tiếp tuyến của (C) tại điểm M có tung độ bằng 4 là : \(y = 9x - 2\)
b) Phương trình tiếp tuyến của (C) tại điểm M là giao của đồ thị hàm số với trục hoành là\(y = x + 2\)
c) Phương trình tiếp tuyến của (C) tại điểm M là giao của đồ thị hàm số với trục tung là:\(y = x + 2\)
d) Phương trình tiếp tuyến của (C) biết tiếp tuyến vuông góc với đường thẳng \((d):y = - x + 1\) là \(y = - \frac{2}{5}x + 1\)
Cho hình chóp S.ABC có SA ⊥ (ABC), SA = h. Gọi M, N, P tương ứng là trung điểm của SA, SB, SC.
a) \(d((MNP),(ABC)) = h\)
b) \(d(NP,(ABC)) = \frac{h}{2}\)
c) \(d(A,(SBC)) = \frac{{ah}}{{\sqrt {{a^2} + {h^2}} }}\)
d) \((MNP)//(ABC)\)
Cho hàm số \(y = \sin x\)
a) Đạo hàm của hàm số là \(y' = - cosx\)
b) Biểu thức \(y'(\frac{\pi }{2}) = 0\)
c) Biểu thức \(y''(\frac{\pi }{2}) = 0\)
d) Biểu thức \({y^{(2024)}} = \sin (x + 1012\pi )\)
Lời giải và đáp án
Cho hàm số \(f(x) = \frac{{{x^3}}}{3} - \frac{3}{2}{x^2} - 4x + 6.\) Phương trình \(f'(x) = 0\) có nghiệm là
-
A.
\(x = - 1\)
-
B.
\(x = 1,\,\,x = 4\)
-
C.
\(x = - 1,\,\,x = 4\)
-
D.
\(x = 0,\,\,x = 3\)
Đáp án : C
Sử dụng công thức đạo hàm.
\(\begin{array}{l}f'(x) = (\frac{{{x^3}}}{3} - \frac{3}{2}{x^2} - 4x + 6)' = {x^2} - 3x - 4\\f'(x) = 0\,\,hay\,\,{x^2} - 3x - 4 = 0 \Leftrightarrow \left[ \begin{array}{l}x = - 1\\x = 4\end{array} \right.\end{array}\)
Đáp án C.
Gọi (d) là tiếp tuyến của đồ thị hàm số\(y = f(x) = - {x^3} + x\) tại điểm \(M( - 2;6).\) Phương trình của (d) là
-
A.
y = -11x +30.
-
B.
y = 13x + 34.
-
C.
y = -11x – 16.
-
D.
y = 13x – 18.
Đáp án : C
Phương trình tiếp tuyến với đồ thị (C): \(y = f(x)\)tại điểm \(M({x_0};f({x_0}))\)là:
\(y = f'({x_0})(x - {x_0}) + f({x_0})\)
Trong đó:
\(M({x_0};f({x_0}))\)gọi là tiếp điểm.
\(k = f'({x_0})\)là hệ số góc.
\(y' = f'(x) = ( - {x^3} + x)' = - 3{x^2} + 1\)
Phương trình tiếp tuyến của đồ thị \(y = f(x) = - {x^3} + x\) tại điểm \(M( - 2;6).\)
\(y = f'( - 2)(x + 2) + 6\,\,hay\,\,y = - 11(x + 2) + 6 = - 11x - 16\)
Đáp án C.
Tính \(\mathop {\lim }\limits_{x \to 3} \frac{{\sqrt {x + 1} - 2}}{{9 - {x^2}}}\) bằng
-
A.
\( - \frac{1}{{24}}\)
-
B.
\( - \frac{1}{6}\)
-
C.
\(\frac{1}{6}\)
-
D.
\(\frac{1}{{24}}\)
Đáp án : A
Nhận biết dạng vô định \(\frac{0}{0}\): Tính \(\mathop {\lim }\limits_{x \to {x_0}} \frac{{f(x)}}{{g(x)}}\)trong đó \(f(x{}_0) = g({x_0}) = 0\)
Khử dạng vô định \(\frac{0}{0}\): Phân tích tử thức và mẫu thức sao cho xuất hiện nhân tử chung \((x - {x_0})\)
\(\mathop {\lim }\limits_{x \to 3} \frac{{\sqrt {x + 1} - 2}}{{9 - {x^2}}} = \mathop {\lim }\limits_{x \to 3} \frac{{x - 3}}{{(\sqrt {x + 1} + 2)(9 - {x^2})}} = \mathop {\lim }\limits_{x \to 3} \frac{{ - 1}}{{(\sqrt {x + 1} + 2)(3 + x)}} = \frac{{ - 1}}{{24}}\)
Đáp án A.
Cho \(u = u\left( x \right),v = v\left( x \right),v\left( x \right) \ne 0\); với k là hằng số. Hãy chọn khẳng định sai?
-
A.
\({\left( {\frac{1}{v}} \right)^\prime } = - \frac{{v'}}{{{v^{}}}}\)
-
B.
\(\left( {u + v} \right)' = u' + v'\)
-
C.
\({\left( {k.u} \right)^\prime } = k.u'\)
-
D.
\(\left( {u.v} \right)' = u'.v + u.v'\)
Đáp án : A
Áp dụng công thức tính đạo hàm
\({\left( {\frac{1}{v}} \right)^\prime } = - \frac{{v'}}{{{v^2}}}\)
\(\left( {u + v} \right)' = u' + v'\)
\({\left( {k.u} \right)^\prime } = k.u'\)
\(\left( {u.v} \right)' = u'.v + u.v'\)
Đáp án A.
Đạo hàm của hàm số \(y = \frac{{2x - 1}}{{1 - x}}\) là
-
A.
\(y' = \frac{3}{{{{\left( { - x + 1} \right)}^2}}}\)
-
B.
\(y' = \frac{1}{{{{\left( {x - 1} \right)}^2}}}\)
-
C.
\(y' = \frac{{ - 1}}{{{{\left( {1 - x} \right)}^2}}}\)
-
D.
\(y' = \frac{{ - 3}}{{{{\left( {1 - x} \right)}^2}}}\)
Đáp án : B
Sử dụng công thức tính đạo hàm của hàm phân thức: \(y' = \left( {\frac{{ax + b}}{{cx + d}}} \right)' = \frac{{ad - bc}}{{{{\left( {cx + d} \right)}^2}}}\)
\(y' = \left( {\frac{{2x - 1}}{{1 - x}}} \right)' = \left( {\frac{{2x - 1}}{{ - x + 1}}} \right)' = \frac{{2.1 - ( - 1).( - 1)}}{{{{( - x + 1)}^2}}} = \frac{1}{{{{( - x + 1)}^2}}}\)
Đáp án B.
Cho hàm số: \(f(x) = \left\{ \begin{array}{l}\frac{{{x^2} - 1}}{{x - 1}}\quad khi\;x \ne 1\\m\quad \quad \quad khi\;x = 1\end{array} \right.\) . Để f(x) liên tục tại điểm \({x_0} = 1\)thì m bằng:
-
A.
-1
-
B.
1
-
C.
2
-
D.
0
Đáp án : C
Bước 1: Tính f(x0) = f2(x0).
Bước 2: Tính \(\mathop {\lim }\limits_{x \to {x_0}} f(x) = \mathop {\lim }\limits_{x \to {x_0}} {f_1}(x) = L\)
Bước 3: Nếu f2(x0) = L thì hàm số f(x) liên tục tại x0.
Nếu f2(x0) ≠ L thì hàm số f(x) không liên tục tại x0.
(Đối với bài toán tìm tham số m để hàm số liên tục tại x0, ta thay bước 3 thành: Giải phương trình L = f2(x0), tìm m)
Hàm số đã cho xác định trên R
Ta có:
\(\begin{array}{l}f(1) = m\\\mathop {\lim }\limits_{x \to 1} f(x) = \mathop {\lim }\limits_{x \to 1} \frac{{{x^2} - 1}}{{x - 1}} = \mathop {\lim }\limits_{x \to 1} \frac{{(x - 1)(x + 1)}}{{x - 1}} = \mathop {\lim }\limits_{x \to 1} (x + 1) = 2\end{array}\)
Ta thấy \(\mathop {\lim }\limits_{x \to 1} f(x) = f(1)\)
Nên m = 2
Vậy khi m = 2 thì hàm số liên tục tại \({x_0} = 1\)
Đáp án C.
Tìm đạo hàm của hàm số sau \(y = {x^4} - 3{x^2} + 2x - 1\)
-
A.
\(y' = 4{x^3} - 3x + 2\)
-
B.
\(y' = 4{x^4} - 6x + 2\)
-
C.
\(y' = 4{x^3} - 6x + 3\)
-
D.
\(y' = 4{x^3} - 6x + 2\)
Đáp án : D
Sử dụng công thức tính đạo hàm của hàm hợp
\(y' = \left( {{x^4} - 3{x^2} + 2x - 1} \right)' = 4{x^3} - 6x + 2\)
Đáp án D.
Cho hàm số \(f(x) = \frac{{a{x^2} + 4x + 3}}{{3x - 2a{x^2}}},(a \in R,a \ne 0)\). Khi đó \(\mathop {\lim }\limits_{x \to - \infty } f(x)\) bằng
-
A.
\( - \frac{1}{2}\)
-
B.
\( + \infty \)
-
C.
\(\frac{a}{3}\)
-
D.
\( - \infty \)
Đáp án : A
Nhận dạng: \(\mathop {\lim }\limits_{x \to \pm \infty } \frac{{f(x)}}{{g(x)}} = \)\(\frac{\infty }{\infty }\) với \(\mathop {\lim }\limits_{x \to \pm \infty } f(x) = \pm \infty ,\mathop {\lim }\limits_{x \to \pm \infty } g(x) = \pm \infty \)
TH1: Nếu f(x) , g(x) là các đa thức thì chia cả tử và mẫu cho lũy thừa cao nhất của x.
TH2: Nếu f(x) , g(x) chứa căn thì có thể chia cả tử và mẫu cho lũy thừa cao nhất của x hoặc nhân lượng liên hợp
\(\mathop {\lim }\limits_{x \to - \infty } f(x) = \mathop {\lim }\limits_{x \to - \infty } \frac{{a{x^2} + 4x + 3}}{{3x - 2a{x^2}}} = \mathop {\lim }\limits_{x \to - \infty } \frac{{{x^2}(a + \frac{4}{x} + \frac{3}{{{x^2}}})}}{{{x^2}(\frac{3}{x} - 2a)}} = \mathop {\lim }\limits_{x \to - \infty } \frac{{a + \frac{4}{x} + \frac{3}{{{x^2}}}}}{{\frac{3}{x} - 2a}} = \frac{a}{{ - 2a}} = - \frac{1}{2}\)
Đáp án A.
Cho hình chóp \(S.ABC\) có đáy ABC là tam giác vuông tại B và SA vuông góc mặt đáy \(\left( {ABC} \right)\), \(SB = 2a\), \(AB = a\)( tham khảo hình vẽ). Tính góc giữa SB và \(mp\left( {ABC} \right)\)
-
A.
\(90^\circ .\)
-
B.
\(60^\circ .\)
-
C.
\(45^\circ .\)
-
D.
\(30^\circ .\)
Đáp án : B
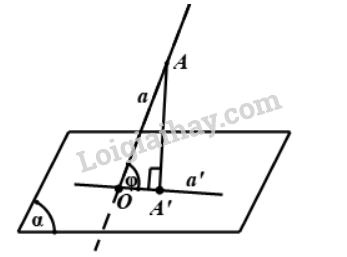
Bước 1: Tìm giao điểm O của đường thẳng a và \(\left( \alpha \right)\)
Bước 2: Xác định hình chiếu A’ của một điểm \(A \in \left( \alpha \right)\) xuống \(\left( \alpha \right)\)
Bước 3: Suy ra: \((a;\left( \alpha \right)) = (a;a') = \widehat {AOA'}\)
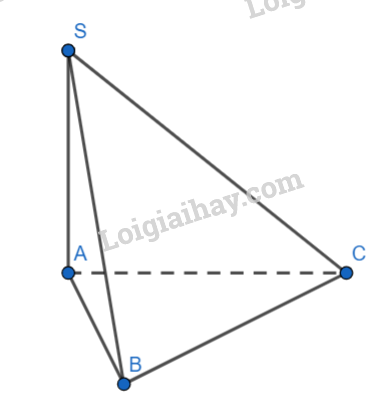
Do \(SA \bot (ABC)\) nên A là hình chiếu của S lên (ABC)
Ta có: \((SB,(ABC)) = (SB,AB) = \widehat {SBA}\)
Xét \(\Delta SAB:c{\rm{os}}\widehat {SBA} = \frac{{AB}}{{SB}} = \frac{a}{{2a}} = \frac{1}{2}\)
Suy ra: \(\widehat {SBA} = {60^0}\)
Đáp án B.
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, cạnh bên SA vuông góc với đáy. Khẳng định nào sau đây đúng?
-
A.
\(AC \bot (SBD)\)
-
B.
\((SCD) \bot (SAD)\)
-
C.
\((SBD) \bot (SAC)\)
-
D.
\((SBC) \bot (SAC)\)
Đáp án : B
Sử dụng định lý đường thẳng vuông góc với mặt phẳng và hai mặt phẳng vuông góc với nhau
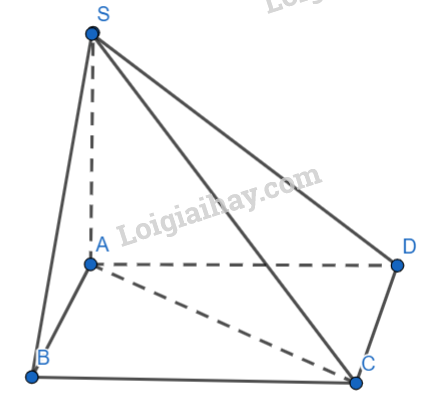
Ta có:
\(\left\{ \begin{array}{l}CD \bot AD\\CD \bot SA\,(do\,\,SA \bot (ABC{\rm{D}}))\\AD,SA \subset (SAD)\\AD \cap SA\end{array} \right. \Rightarrow CD \bot (SAD)\)
Mặt khác:
\(CD \subset (SCD) \Rightarrow (SCD) \bot (SAD)\)
Đáp án B.
Cho hình chóp S.ABCD có đáy ABCD là hình thoi tâm O và SA = SC, SB = SD. Khẳng định nào sau đây đúng ?
-
A.
\(AC \bot (SBD)\)
-
B.
\(AB \bot (SAD)\)
-
C.
\(AC \bot (SBD)\)
-
D.
\(SO \bot (ABCD)\)
Đáp án : C
Sử dụng định lý đường thẳng vuông góc với mặt phẳng
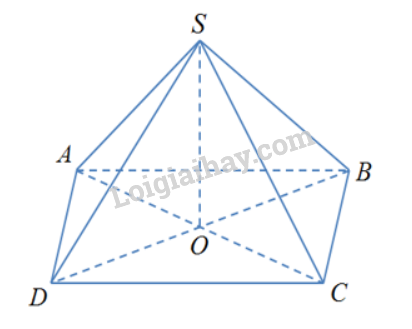
Ta có:
\(\left\{ \begin{array}{l}AC \bot BD\\AC \bot SO\\BD,SO \subset (SBD)\\BD \cap SO\end{array} \right. \Rightarrow AC \bot (SBD)\)
Đáp án C.
Với hàm số \(g\left( x \right) = \frac{{\left( {2x + 1} \right){{\left( {2 - 3x} \right)}^2}}}{{x - 1}};\,g'\left( 2 \right)\) bằng
-
A.
232.
-
B.
72.
-
C.
152.
-
D.
-75.
Đáp án : B
Sử dụng phương tính đạo hàm của hàm hợp
\(\begin{array}{l}g'\left( x \right) = \frac{{\left[ {\left( {2x + 1} \right){{\left( {2 - 3x} \right)}^2}} \right]'(x - 1) - \left( {2x + 1} \right){{\left( {2 - 3x} \right)}^2}.(x - 1)'}}{{{{\left( {x - 1} \right)}^2}}} = \frac{{\left[ {2{{\left( {2 - 3x} \right)}^2} + (2x + 1).2\left( {2 - 3x} \right).( - 3)} \right] + \left( {2x + 1} \right){{\left( {2 - 3x} \right)}^2}}}{{{{\left( {x - 1} \right)}^2}}}\\ = \frac{{3x(3x - 2)(4x - 5)}}{{{{\left( {x - 1} \right)}^2}}}\\ \Rightarrow g'\left( 2 \right) = \frac{{3x(3x - 2)(4x - 5)}}{{{{\left( {x - 1} \right)}^2}}} = 72\end{array}\)
Đáp án B.
Trong một chiếc hộp có 20 viên bi, trong đó có 8 viên bi màu đỏ, 7 viên bi màu xanh và 5 viên bi màu vàng. Lấy ngẫu nhiên ra 3 viên bi
a) Xác suất để 3 viên bi lấy ra đều màu đỏ là \(\frac{{14}}{{285}}\)
b) Xác suất để 3 viên bi lấy ra có không quá hai màu là \(\frac{{43}}{{57}}\)
c) Xác suất để 3 viên bi lấy ra đều có màu vàng là \(\frac{1}{7}\)
d) Xác suất để 3 viên bi lấy ra có đủ cả ba màu là \(\frac{{14}}{{57}}\)
a) Xác suất để 3 viên bi lấy ra đều màu đỏ là \(\frac{{14}}{{285}}\)
b) Xác suất để 3 viên bi lấy ra có không quá hai màu là \(\frac{{43}}{{57}}\)
c) Xác suất để 3 viên bi lấy ra đều có màu vàng là \(\frac{1}{7}\)
d) Xác suất để 3 viên bi lấy ra có đủ cả ba màu là \(\frac{{14}}{{57}}\)
Sử dụng các quy tắc đếm để xác định số phần tử của không gian mẫu và biến cố
Không gian mẫu: \((\Omega ) = C_{20}^3 = 1140\)
a) Gọi A là biến cố: “3 viên bi lấy ra đều màu đỏ”; \(P(A) = \frac{{n(A)}}{{n(\Omega )}} = \frac{{C_8^3}}{{C_{20}^3}} = \frac{{56}}{{1140}} = \frac{{14}}{{285}}\)
b) B là biến cố: “3 viên bi lấy ra có không quá hai màu”
TH1: Số cách lấy ra 3 viên bi lấy ra chỉ có một màu: \(C_8^3 + C_7^3 + C_5^3 = 101\)
TH2: Số cách lấy ra 3 viên bi lấy ra chỉ có đúng hai màu: \(\left[ {C_{15}^3 - \left( {C_8^3 + C_7^3} \right)} \right] + \left[ {C_{13}^3 - \left( {C_8^3 + C_5^3} \right)} \right] + \left[ {C_{12}^3 - \left( {C_5^3 + C_7^3} \right)} \right] = 759\)
Nên: \(P(B) = \frac{{n(B)}}{{n(\Omega )}} = \frac{{101 + 759}}{{1140}} = \frac{{43}}{{57}}\)
c) C là biến cố: “3 viên bi lấy ra đều có màu vàng”; \(P(C) = \frac{{n(C)}}{{n(\Omega )}} = \frac{{C_5^3}}{{C_{20}^3}} = \frac{{10}}{{1140}} = \frac{1}{{114}}\)
d) D là biến cố: “3 viên bi lấy ra có đủ cả ba màu”: \(P(D) = \frac{{n(D)}}{{n(\Omega )}} = \frac{{C_8^1.C_7^1.C_5^1}}{{C_{20}^3}} = \frac{{280}}{{1140}} = \frac{{14}}{{57}}\)
Cho hàm số có đồ thị (C): \(y = f(x) = \frac{{x - 2}}{{x - 1}}\)
a) Phương trình tiếp tuyến của (C) tại điểm M có tung độ bằng 4 là : \(y = 9x - 2\)
b) Phương trình tiếp tuyến của (C) tại điểm M là giao của đồ thị hàm số với trục hoành là\(y = x + 2\)
c) Phương trình tiếp tuyến của (C) tại điểm M là giao của đồ thị hàm số với trục tung là:\(y = x + 2\)
d) Phương trình tiếp tuyến của (C) biết tiếp tuyến vuông góc với đường thẳng \((d):y = - x + 1\) là \(y = - \frac{2}{5}x + 1\)
a) Phương trình tiếp tuyến của (C) tại điểm M có tung độ bằng 4 là : \(y = 9x - 2\)
b) Phương trình tiếp tuyến của (C) tại điểm M là giao của đồ thị hàm số với trục hoành là\(y = x + 2\)
c) Phương trình tiếp tuyến của (C) tại điểm M là giao của đồ thị hàm số với trục tung là:\(y = x + 2\)
d) Phương trình tiếp tuyến của (C) biết tiếp tuyến vuông góc với đường thẳng \((d):y = - x + 1\) là \(y = - \frac{2}{5}x + 1\)
Bước 1: Gọi M(x0; f(x0)) là tọa độ tiếp điểm của tiếp tuyến của (C) thì f'(x0) = k
Bước 2: Giải phương trình f'(x0) = k với ẩn là x0.
Bước 3: Phương trình tiếp tuyến của (C) có dạng y = k(x – x0) + f(x0)
\(y' = f'(x) = \left( {\frac{{x - 2}}{{x - 1}}} \right)' = \frac{1}{{{{\left( {x - 1} \right)}^2}}}\)
a) Gọi \(M({x_0};{y_0})\) là tiếp điểm. M có tung độ bằng 4 nên \(M(\frac{2}{3};4)\)
Gọi k là hệ số góc của tiếp tuyển tại M nên \(k = f'\left( {\frac{2}{3}} \right) = 9\)
Phương trình tiếp tuyến của (C) tại điểm \(M(\frac{2}{3};4)\) là \(y = 9(x - \frac{2}{3}) + 4\,\,hay\,\,y = 9x - 2\)
b) Gọi \(M({x_0};{y_0})\) là tiếp điểm. M là giao của đồ thị với trục hoành nên \(M(2;0)\)
Gọi k là hệ số góc của tiếp tuyến tại M nên \(k = f'\left( 2 \right) = 1\)
Phương trình tiếp tuyến của (C) (C) tại điểm \(M(2;0)\) là \(\,y = x - 2\)
c) Gọi \(M({x_0};{y_0})\) là tiếp điểm.
M là giao điểm của đồ thị với trục tung nên \(M(0;2)\)
Gọi k là hệ số góc của tiếp tuyến tại M. Khi đó \(k = f'\left( 0 \right) = 1\)
Phương trình tiếp tuyến tại M là: \(\,y = (x - 0) + 2\,\,hay\,\,y = x + 2\)
d) Gọi k là hệ số góc của tiếp tuyến của đồ thị (C)
Do tiếp tuyến vuông góc với \((d):y = - x + 1\) nên \( - 1.k = - 1 \Leftrightarrow k = 1\)
Gọi \(M({x_0},{y_0}) \in (C)\)mà tiếp tuyến của (C) tại M có hệ số góc k = 1
\(f'({x_0}) = 1 \Rightarrow \frac{1}{{{{(x - 1)}^2}}} = 1 \Leftrightarrow \left[ \begin{array}{l}{x_0} = 2\\{x_0} = 0\end{array} \right.\)
* Với \({x_0} = 2\) ta có \({y_0} = f(2) = 0 \Rightarrow {M_1}(2;0) \in (C)\)
Phương trình tiếp tuyến của (C) tại \({M_1}(2;0)\)) là \(y = x - 2\)
* Với \({x_0} = 0\) ta có \({y_0} = f(0) = 2 \Rightarrow {M_2}(0;2) \in (C)\)
Phương trình tiếp tuyến của (C) tại \({M_2}(0;2)\) là \(\,y = x + 2\)
Cho hình chóp S.ABC có SA ⊥ (ABC), SA = h. Gọi M, N, P tương ứng là trung điểm của SA, SB, SC.
a) \(d((MNP),(ABC)) = h\)
b) \(d(NP,(ABC)) = \frac{h}{2}\)
c) \(d(A,(SBC)) = \frac{{ah}}{{\sqrt {{a^2} + {h^2}} }}\)
d) \((MNP)//(ABC)\)
a) \(d((MNP),(ABC)) = h\)
b) \(d(NP,(ABC)) = \frac{h}{2}\)
c) \(d(A,(SBC)) = \frac{{ah}}{{\sqrt {{a^2} + {h^2}} }}\)
d) \((MNP)//(ABC)\)
Sử dụng phương pháp tính khoảng cách từ điểm đến mặt phẳng và khoảng cách từ đường thẳng đến mặt phẳng
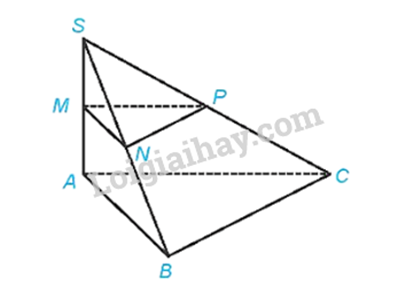
a) Xét tam giác SAB có M là trung điểm của SA, N là trung điểm của SB nên MN là đường trung bình của tam giác SAB. Suy ra \(MN//AB\),do đó \(MN//(ABC)\)
Xét tam giác SBC có N là trung điểm của SB, P là trung điểm của SC nên PN là đường trung bình của tam giác SBC. Suy ra \(PN//BC\),do đó \(PN//(ABC)\)
Khi đó, \(d((MNP),(ABC)) = d(M,(ABC))\)
Vì \(SA \bot (ABC)\) nên \(MA \bot (ABC)\). Do đó \(d(M,(ABC)) = MA\)
Vì M là trung điểm SA nên \(AM = \frac{{SA}}{2} = \frac{h}{2}\)
Do đó \(d((MNP),(ABC)) = \frac{h}{2}\)
b) Vì \(PN//(ABC)\) nên \(d(NP,(ABC)) = d(N,(ABC))\)
Vì \(MN//(ABC)\) nên \(d(N,(ABC)) = d(M,(ABC)) = MA = \frac{h}{2}\)
Vậy \(d(N,(ABC)) = \frac{h}{2}\)
c) Vì tam giác ABC là tam giác vuông tại B nên \(BC \bot AB\)
Vì \(SA \bot (ABC)\) nên \(SA \bot BC\)mà \(BC \bot AB\) nên \(BC \bot (SAB)\), suy ra \((SBC) \bot (SAB)\)
Kẻ \(AH \bot SB\) tại H
Vì \(\left\{ \begin{array}{l}(SBC) \bot (SAB)\\(SBC) \cap (SAB) = SB\\AH \subset (SAB)\\AH \bot SB\end{array} \right. \Rightarrow AH \bot (SBC)\)
Khi đó \(d(A,(SBC)) = AH\)\(\)
Vì \(SA \bot (SBC)\) nên \(SA \bot AB\)
Xét tam giác SAB vuông tại A, AH là đường cao, có:
\(\frac{1}{{A{H^2}}} = \frac{1}{{S{A^2}}} + \frac{1}{{A{B^2}}} = \frac{1}{{{h^2}}} + \frac{1}{{{a^2}}} = \frac{{{a^2} + {h^2}}}{{{a^2}{h^2}}} \Rightarrow AH = \frac{{ah}}{{\sqrt {{a^2} + {h^2}} }}\)
Vậy \(d(A,(SBC)) = \frac{{ah}}{{\sqrt {{a^2} + {h^2}} }}\)
d)\(MN//(ABC)\) mà \(MN \subset (MNP) \Rightarrow (MNP)//(ABC)\)
Cho hàm số \(y = \sin x\)
a) Đạo hàm của hàm số là \(y' = - cosx\)
b) Biểu thức \(y'(\frac{\pi }{2}) = 0\)
c) Biểu thức \(y''(\frac{\pi }{2}) = 0\)
d) Biểu thức \({y^{(2024)}} = \sin (x + 1012\pi )\)
a) Đạo hàm của hàm số là \(y' = - cosx\)
b) Biểu thức \(y'(\frac{\pi }{2}) = 0\)
c) Biểu thức \(y''(\frac{\pi }{2}) = 0\)
d) Biểu thức \({y^{(2024)}} = \sin (x + 1012\pi )\)
Sử dụng công thức tính đạo hàm của hàm số lượng giác
a) \(y' = (\sin x)' = cosx\)
b) \(y'(\frac{\pi }{2}) = \cos \frac{\pi }{2} = 0\)
c) \(\begin{array}{l}y'' = \left( {cosx} \right)' = - \sin x\\y''\left( {\frac{\pi }{2}} \right) = - 1\end{array}\)
d) \(\begin{array}{l}{y^{(n)}} = \sin (x + n\frac{\pi }{2})\\{y^{(2024)}} = \sin (x + 1012\pi )\end{array}\)
Sử dụng phương pháp nhân liên hợp và phân tích thành nhân tử
\(\mathop {lim}\limits_{x \to 2} \frac{{\sqrt {4x + 1} - 3}}{{x - 2}} = \mathop {lim}\limits_{x \to 2} \frac{{4x - 8}}{{\left( {x - 2} \right)\left( {\sqrt {4x + 1} + 3} \right)}} = \mathop {lim}\limits_{x \to 2} \frac{{4(x - 2)}}{{\left( {x - 2} \right)\left( {\sqrt {4x + 1} + 3} \right)}} = \mathop {lim}\limits_{x \to 2} \frac{4}{{\left( {\sqrt {4x + 1} + 3} \right)}} = \frac{2}{3}\)
Sử dụng công thức tính đạo hàm của hàm hợp
\(\begin{array}{l}y' = \left[ {{{\left( {{x^4} - 1} \right)}^4}} \right]' = 4.{\left( {{x^4} - 1} \right)^3}.4{x^3} = 16{x^3}{\left( {{x^4} - 1} \right)^3}\\y'(1) = 0\end{array}\)
Bước 1: Tính \(f({x_0}) = {f_2}({x_0})\)
Bước 2: Tính \(\mathop {\lim }\limits_{x \to {x_0}} f(x) = \mathop {\lim }\limits_{x \to {x_0}} {f_1}(x) = L\)
Bước 3: Nếu \({f_2}({x_0}) = L\) thì hàm số f(x) liên tục tại \({x_0}\)
Nếu \({f_2}({x_0}) \ne L\)thì hàm số f(x) không liên tục tại \({x_0}\).
(Đối với bài toán tìm tham số m để hàm số liên tục tại x0, ta thay bước 3 thành: Giải phương trình L = f2(x0), tìm m)
Hàm số đã cho xác định trên R
Ta có: \(f(1) = 1 - m\)
\(\mathop {\lim }\limits_{x \to 1} f(x) = \mathop {\lim }\limits_{x \to 1} \frac{{{x^2} - 3x + 2}}{{x - 1}} = \mathop {\lim }\limits_{x \to 1} \frac{{(x - 1)(x - 2)}}{{x - 1}} = \mathop {\lim }\limits_{x \to 1} (x - 2) = - 1\)
Để hàm số liên tục tại x = 1 khi \(f(1) = \mathop {\lim }\limits_{x \to 1} \frac{{{x^2} - 3x + 2}}{{x - 1}} \Leftrightarrow 1 - m = - 1 \Leftrightarrow m = 2\)
Sử dụng phương pháp tính góc giữa hai mặt phẳng
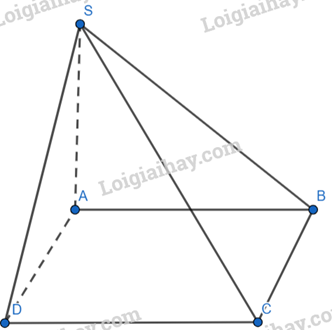
\(\begin{array}{l}\left\{ \begin{array}{l}BC \bot AB\,\\BC \bot SA\,\,(Do\,\,SA \bot (ABCD))\\AB,SA \subset (SAB)\\AB \cap SA\end{array} \right. \Rightarrow BC \bot (SAB)\\ \Rightarrow BC \bot SB\end{array}\)\(SA \bot (ABCD) \Rightarrow SA \bot AB\)
Ta có: \(\left\{ \begin{array}{l}(SBC) \cap (ABCD) = BC\\SB \subset (SBC),SB \bot BC\\AB \subset (ABCD),AB \bot BC\end{array} \right. \Rightarrow \left( {(SBC),(ABCD)} \right) = (SB,AB)\)
Do \(SA \bot (ABCD) \Rightarrow SA \bot AB\). Xét tam giác SAB vuông tại A có:
\(\tan (SB,AB) = \tan \widehat {SBA} = \frac{{SA}}{{AB}} = \frac{{a\sqrt 2 }}{a} = \sqrt 2 \)
Lập biểu thức tính khoảng cách từ điểm \(I( - 1;2)\) tới tiếp tuyển của đồ thị
Sử dụng BĐT Cauchy để tìm giá trị lớn nhất của biểu thức
Giả sử \(M({x_0};2 - \frac{3}{{{x_0} + 1}}) \in (C)\). PTTT của (C) tại M là:
\(y = \frac{3}{{{{({x_0} + 1)}^2}}}(x - {x_0}) + 2 - \frac{3}{{{x_0} + 1}}\,\,\,(\Delta )\)
Hay \(\begin{array}{l}(\Delta ):\,\,\,\frac{3}{{{{({x_0} + 1)}^2}}}x - y + \left[ {\frac{{3{x_0}}}{{{{({x_0} + 1)}^2}}} + 2 - \frac{3}{{{x_0} + 1}}} \right] = 0\,\,\,\\(\Delta ):\,\frac{3}{{{{({x_0} + 1)}^2}}}x - y + 2 - \frac{3}{{{{({x_0} + 1)}^2}}} = 0\\d(I,\Delta ) = \frac{{|\frac{3}{{{{({x_0} + 1)}^2}}}{x_0} - (2 - \frac{3}{{{x_0} + 1}}) + 2 - \frac{3}{{{{({x_0} + 1)}^2}}}|}}{{\sqrt {\frac{9}{{{{({x_0} + 1)}^4}}} + 1} }} = \frac{{6|{x_0} + 1|}}{{\sqrt {9 + {{({x_0} + 1)}^4}} }} = \frac{6}{{\sqrt {\frac{9}{{{{({x_0} + 1)}^2}}} + {{({x_0} + 1)}^2}} }}\end{array}\)
Áp dụng BĐT Cauchy: \(\frac{9}{{{{({x_0} + 1)}^2}}} + {({x_0} + 1)^2} \ge 2\sqrt 9 = 6 \Rightarrow d \le \sqrt 6 \)
Dấu “=” xảy ra khi \(\frac{9}{{{{({x_0} + 1)}^2}}} = {({x_0} + 1)^2} \Leftrightarrow {x_0} = - 1 \pm \sqrt 3 \)
Vậy có hai điểm cần tìm là \(M( - 1 + \sqrt 3 ;2 - \sqrt 3 )\) hoặc \(M( - 1 - \sqrt 3 ;2 + \sqrt 3 )\)
Lượng thức ăn mà trang trại ăn hết ở ngày thứ k là: \(M{(1 + r\% )^{k - 1}},k \in N*\)
Trong đó:
M: là lượng thứ ăn trang trại ăn hết trong mỗi ngày
r (%): là % mức tiêu thụ thức ăn tăng thêm mỗi ngày
Theo dự định, mỗi ngày, trang trại ăn hết: \(1:50 = \frac{1}{{50}}\)(lượng thức ăn)
Lượng thức ăn mà trang trại ăn hết ở ngày thứ k là: \(\frac{1}{{50}}{(1 + 3\% )^{k - 1}},k \in N*\)
Xác định số tự nhiên n nhỏ nhât để:
\(\begin{array}{l}\frac{1}{{50}} + \frac{1}{{50}}(1 + 3\% ) + \frac{1}{{50}}{(1 + 3\% )^2} + ... + \frac{1}{{50}}{(1 + 3\% )^{n - 1}} \ge 1\\ \Leftrightarrow \frac{1}{{50}}(1 + 1,03 + 1,{03^2} + ... + 1,{03^{n - 1}}) \ge 1\\ \Leftrightarrow \frac{1}{{50}}.\frac{{1,{{03}^{n - 1}} - 1}}{{1,03 - 1}} \ge 1 \Leftrightarrow 1,{03^{n - 1}} - 1 \ge 1,5 \Leftrightarrow 1,{03^{n - 1}} \ge 2,5 \Leftrightarrow n - 1 \ge {\log _{1,03}}2,5 \Leftrightarrow n \ge 31,99 \Rightarrow {n_{Min}} = 32\end{array}\)
Phần I. Câu trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi thí sinh chỉ chọn một phương án.
Phần I. Câu trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi thí sinh chỉ chọn một phương án.
Phần I. Câu trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi thí sinh chỉ chọn một phương án.
Phần I. Trắc nghiệm. Hãy chọn phương án trả lời đúng và viết chữ cái đứng trước đáp án đó vào bài làm.
Phần I. Trắc nghiệm. Hãy chọn phương án trả lời đúng và viết chữ cái đứng trước đáp án đó vào bài làm.
Câu 1: Với b,c là hai số thực dương tùy ý thỏa mãn \({\rm{lo}}{{\rm{g}}_5}b \ge {\rm{lo}}{{\rm{g}}_5}c\), khẳng định nào dưới đây là đúng? A. \(b \ge c\). B. \(b \le c\). C. \(b > c\). D. \(b < c\).
Phần I. Câu trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi thí sinh chỉ chọn một phương án.
A. NỘI DUNG ÔN TẬP I. Đại số 1. Hàm số mũ và hàm số logarit - Lũy thừa với số mũ thực - Logarit - Hàm số mũ và hàm số logarit - Phương trình, bất phương trình mũ và logarit
>> Học trực tuyến Lớp 11 cùng thầy cô giáo giỏi trên Tuyensinh247.com. Bứt phá điểm 9,10 chỉ sau 3 tháng. Cam kết giúp học sinh lớp 11 học tốt, hoàn trả học phí nếu học không hiệu quả.
 |
 |
 |
 |
 |
 |
 |
 |
