 Đề thi toán 11, đề kiểm tra toán 11 kết nối tri thức với cuộc sống có đáp án và lời giải chi tiết
Đề thi toán 11, đề kiểm tra toán 11 kết nối tri thức với cuộc sống có đáp án và lời giải chi tiết
 Đề thi giữa kì 1 Toán 11 - Kết nối tri thức
Đề thi giữa kì 1 Toán 11 - Kết nối tri thức Đề thi giữa kì 1 Toán 11 Kết nối tri thức - Đề số 3
Câu 1: Đường tròn lượng giác có bán kính bằng:
Đề bài
Phần trắc nghiệm (4 điểm)
Câu 1: Đường tròn lượng giác có bán kính bằng:
|
A. \(2\) |
B. \(1\) |
|
C. \(\frac{\pi }{2}\) |
D. \(\pi \) |
Câu 2: Cho \(\sin a = \frac{1}{3}\). Giá trị của biểu thức \(A = \frac{{\cot a - \tan a}}{{\tan a + 2\cot a}}\) bằng:
|
A. \(\frac{1}{9}\) |
B. \(\frac{7}{9}\) |
|
C. \(\frac{{17}}{{81}}\) |
D. \(\frac{7}{{17}}\) |
Câu 3: Trong các công thức sau, công thức nào đúng?
|
A. \(\sin \left( {a-b} \right) = \sin a.\cos b - \cos a.\sin b.\). |
B. \(\cos \left( {a-b} \right) = \cos a.\cos b - \sin a.\sin b.\). |
|
C. \(\sin \left( {a + b} \right) = \sin a.\cos b - \cos a.\sin b.\). |
D. \(\cos \left( {a + b} \right) = \cos a.\cos b + \sin a.\sin b.\). |
Câu 4: Mệnh đề nào sau đây đúng?
|
A. \(\cos 2a = {\cos ^2}a - {\sin ^2}a\) |
B. \(\cos 2a = {\cos ^2}a + {\sin ^2}a\) |
|
C. \(\cos 2a = 2{\cos ^2}a + 1\) |
D. \(\cos 2a = 2{\sin ^2}a - 1\) |
Câu 5: Hàm số nào sau đây là hàm số chẵn?
|
A. \(y = - 2\cos x\) |
B. \(y = - 2\sin x\) |
|
C. \(y = 2\sin \left( { - x} \right)\) |
D. \(y = \sin x - \cos x\) |
Câu 6: Hình nào dưới đây biểu diễn đồ thị hàm số \(y = f(x) = 2\sin 2x?\)
|
A. |
B. |
|
C. |
D. |
Câu 7: Nghiệm của phương trình \(\cos x = \frac{1}{2}\) là:
|
A. \(x = \pm \frac{\pi }{2} + k2\pi \) |
B. \(x = \pm \frac{\pi }{3} + k2\pi \) |
|
C. \(x = \pm \frac{\pi }{4} + k2\pi \) |
D. \(x = \pm \frac{\pi }{6} + k2\pi \) |
Câu 8: Trên đoạn \(\left[ {0;2018\pi } \right]\), phương trình \(\sqrt 3 \cot x - 3 = 0\) có số nghiệm là :
|
A. \(2018.\) |
B. \(6340.\) |
|
C. \(2017.\) |
D. \(6339.\) |
Câu 9: Cho dãy số có các số hạng đầu là: \(\frac{1}{3};\,\frac{1}{{{3^2}}};\,\frac{1}{{{3^3}}};\,\frac{1}{{{3^4}}};\,\frac{1}{{{3^5}}};\,...\)Số hạng tổng quát của dãy số này là?
|
A. \({u_n} = \frac{1}{3}.\frac{1}{{{3^{n + 1}}}}\) |
B. \({u_n} = \frac{1}{{{3^{n + 1}}}}\) |
|
C. \({u_n} = \frac{1}{{{3^n}}}\) |
D. \({u_n} = \frac{1}{{{3^{n - 1}}}}\) |
Câu 10: Cho dãy số \(\left( {{u_n}} \right)\) xác định bởi \(\left\{ \begin{array}{l}{u_1} = 2\\{u_{n + 1}} = \frac{1}{3}\left( {{u_n} + 1} \right)\end{array} \right..\) Tìm số hạng \({u_4}.\)
|
A. \({u_4} = \frac{5}{9}.\) |
B. \({u_4} = 1.\) |
|
C. \({u_4} = \frac{2}{3}.\) |
D. \({u_4} = \frac{{14}}{{27}}.\) |
Câu 11: Trong các dãy số sau đây, dãy số nào là cấp số cộng?
|
A. \({u_n} = {3^n}\) |
B. \({u_n} = {\left( { - 3} \right)^{n + 1}}\) |
|
C. \({u_n} = 3n + 1\) |
D. \({u_n} = {2^{n + 1}}\) |
Câu 12: Cho cấp số cộng \(\left( {{u_n}} \right)\) và gọi \({S_n}\) là tổng \(n\) số hạng đầu tiên của nó. Biết \({u_{21}} = - 19\) và \({S_{22}} = 0\). Tìm số hạng tổng quát \({u_n}\) của cấp số cộng đó.
|
A. \({u_n} = 21 + 2n\) |
B. \({u_n} = 21 - 2n\) |
|
C. \({u_n} = 23 - 2n\) |
D. \({u_n} = 23 + 2n\) |
Câu 13: Hùng đang tiết kiệm để mua một cây đàn piano có giá 142 triệu đồng. Trong tháng đầu tiên, anh ta để dành được 20 triệu đồng. Mỗi tháng tiếp theo anh ta để dành được 3 triệu đồng và đưa số tiền tiết kiệm của mình. Hỏi ít nhất vào tháng thứ bao nhiêu thì Hùng mới có đủ tiền để mua cây đàn piano đó?
|
A. \(43\) |
B. \(41\) |
|
C. \(40\) |
D. \(42\) |
Câu 14: Trong các dãy số cho dưới đây, dãy số nào là cấp số nhân?
|
A. \(1;\,2;\,3;\,4;\,5\) |
B. \(1;\,3;\,6;\,9;\,12\) |
|
C. \(2;\,4;\,6;\,8;\,10\) |
D. \(2;\,2;\,2;\,2;\,2\) |
Câu 15: Cho cấp số nhân \(\left( {{u_n}} \right)\) có số hạng đầu \({u_1} = 2\) và \({u_6} = 486\). Công bội q bằng
|
A. \(q = 3\) |
B. \(q = 5\) |
|
C. \(q = \frac{3}{2}\) |
D. \(q = \frac{2}{3}\) |
Câu 16: Cho \(\left( {{u_n}} \right)\) là cấp số nhân, đặt \({S_n} = {u_1} + {u_2} + ... + {u_n}\). Biết \({S_2} = 4;\,{S_3} = 13\)và \({u_2} < 0\), giá trị \({S_5}\) bằng
|
A. \(2\) |
B. \(\frac{{181}}{{16}}\) |
|
C. \(\frac{{35}}{{16}}\) |
D. \(121\) |
Câu 17: Cho mẫu số liệu ghép nhóm về thời gian (phút) đi từ nhà đến nơi làm việc của các nhân viên một công ty như sau:
|
Thời gian |
\(\left[ {15;20} \right)\) |
\(\left[ {20;25} \right)\) |
\(\left[ {25;30} \right)\) |
\(\left[ {30;35} \right)\) |
\(\left[ {35;40} \right)\) |
\(\left[ {40;45} \right)\) |
\(\left[ {45;50} \right)\) |
|
Số nhân viên |
6 |
14 |
25 |
37 |
21 |
13 |
9 |
Có bao nhiêu nhân viên có thời gian đi từ nhà đến nơi làm việc là từ 15 phút đến dưới 20 phút?
|
A. 6 |
B. \(9\) |
|
C. 14 |
D. 13 |
Câu 18: Cho mẫu số liệu ghép nhóm sau:
|
Nhóm |
\(\left[ {{a_1};{a_2}} \right)\) |
. |
\(\left[ {{a_i};{a_{i + 1}}} \right)\) |
. |
\(\left[ {{a_k};{a_{k + 1}}} \right)\) |
|
Tần số |
\({m_1}\) |
. |
\({m_i}\) |
. |
\({m_k}\) |
Với \(n = {m_1} + {m_2} + ... + {m_k}\) là cỡ mẫu và \({x_i} = \frac{{{a_i} + {a_{i + 1}}}}{2}\) (\(i = 1,...k\)) là giá trị đại diện của nhóm \(\left[ {{a_i};{a_{i + 1}}} \right)\). Khi đó công thức tính số trung bình cộng của mẫu số liệu ghép nhóm trên là:
|
A. \(\bar x = \frac{n}{{{m_1}{x_1} + \ldots + {m_k}{x_k}}}\) |
B. \(\bar x = \frac{{\left( {{m_1}{x_1}} \right) \ldots \left( {{m_k}{x_k}} \right)}}{n}\) |
|
C. \(\bar x = \frac{{{m_1}{x_1} - \ldots - {m_k}{x_k}}}{n}\) |
D. \(\bar x = \frac{{{m_1}{x_1} + \ldots + {m_k}{x_k}}}{n}\) |
Câu 19: Thời gian luyện tập trong một ngày (tính theo giờ) của một số vận động viên được ghi lại ở bảng sau:

Tứ phân vị thứ ba của mẫu số liệu trên gần nhất với giá trị nào trong các giá trị sau?
|
A. 3 |
B. 4 |
|
C. 7 |
D. 5 |
Câu 20: Trong một hội thao, thời gian chạy \(200{\rm{\;m}}\) của một nhóm các vận động viên được ghi lại ở bảng sau:

Trung vị của mẫu số liệu ghép nhóm trên thuộc khoảng nào trong các khoảng dưới đây?
|
A. \(\left[ {20;30} \right)\) |
B. \(\left[ {30;40} \right)\) |
|
C. \(\left[ {50;60} \right)\) |
D. \(\left[ {60;70} \right)\) |
Phần tự luận (6 điểm)
Bài 1. (1 điểm)
Tìm giá trị lớn nhất và giá trị nhỏ nhất : \(y = {\tan ^2}x - \tan x + 1\) với \(x \in \left[ { - \frac{\pi }{4};\,\frac{\pi }{4}} \right]\).
Bài 2. (1,5 điểm)
a) Giải phương trình \(\cot \;x = \sqrt 3 \)
b) Trong khoảng \(\left( {0;\pi } \right)\), phương trình \(\cos 4x + \sin x = 0\) có tập nghiệm là \(S\). Tìm S.
c) Giải phương trình \(\frac{3}{2} - 3cos4x = 6sinx.sin3x\).
Bài 3. (2 điểm)
a) Một cơ sở khoan giếng đưa ra định mức giá như sau : Giá từ mét khoan đầu tiên là \(100000\) đồng và kể từ mét khoan thứ hai, giá mỗi mét tăng thêm \(30000\) đồng so với giá của mét khoan ngay trước đó. Một người muốn kí hợp đồng với cơ sở khoan giếng này để khoan giếng sâu \(20\) mét lấy nước dùng cho sinh hoạt gia đình. Hỏi sau khi hoàn thành việc khoan giếng, gia đình đó phải thanh toán cho cơ sở khoan giếng số tiền bằng bao nhiêu?
b) Cho cấp số nhân \(\left( {{x_n}} \right)\) có \({x_2} = - 3\) và \({x_4} = - 27.\) Tính số hạng đầu \({x_1}\) và công bội \(q\) của cấp số nhân
Bài 4. (1,5 điểm)
Một người thống kê lại thời gian thực hiện các cuộc gọi điện thoại của người đó trong một tuần ở bảng sau:

a) Tính trung vị của mẫu số liệu ghép nhóm này.
b) Tìm tứ phân vị thứ nhất và tứ phân vị thứ ba của mẫu số liệu ghép nhóm này.
---- Hết ----
Lời giải chi tiết
Phần trắc nghiệm (4 điểm)
|
Câu 1: B |
Câu 2: D |
Câu 3: A |
Câu 4: A |
Câu 5: A |
Câu 6: C |
Câu 7: B |
Câu 8: A |
Câu 9: C |
Câu 10: A |
|
Câu 11: C |
Câu 12: C |
Câu 13: D |
Câu 14: D |
Câu 15: A |
Câu 16: B |
Câu 17: A |
Câu 18: D |
Câu 19: C |
Câu 20: A |
Câu 1: Đường tròn lượng giác có bán kính bằng:
|
A. \(2\) |
B. \(1\) |
|
C. \(\frac{\pi }{2}\) |
D. \(\pi \) |
Phương pháp
Đường tròn lượng giác có bán kính bằng 1.
Lời giải
Đường tròn lượng giác có bán kính bằng 1.
Đáp án B
Câu 2: Cho \(\sin a = \frac{1}{3}\). Giá trị của biểu thức \(A = \frac{{\cot a - \tan a}}{{\tan a + 2\cot a}}\) bằng:
|
A. \(\frac{1}{9}\) |
B. \(\frac{7}{9}\) |
|
C. \(\frac{{17}}{{81}}\) |
D. \(\frac{7}{{17}}\) |
Phương pháp
B1: Biến đổi biểu thức A để xuất hiện giả thiết .
B2: Thay \(\sin a = \frac{1}{3}\) vào biểu thức A sau đó rút gọn.
Lời giải
Ta có: \(A = \frac{{\cot a - \tan a}}{{\tan a + 2\cot a}} = \frac{{\frac{{\cos a}}{{\sin a}} - \frac{{\sin a}}{{\cos a}}}}{{\frac{{\sin a}}{{\cos a}} + 2\frac{{\cos a}}{{\sin a}}}} = \frac{{{{\cos }^2}a - {{\sin }^2}a}}{{{{\sin }^2}a + 2{{\cos }^2}a}}\)\( = \frac{{\left( {1 - {{\sin }^2}a} \right) - {{\sin }^2}a}}{{{{\sin }^2}a + 2\left( {1 - {{\sin }^2}a} \right)}} = \frac{{1 - 2{{\sin }^2}a}}{{2 - {{\sin }^2}a}} = \frac{7}{{17}}\).
Đáp án D
Câu 3: Trong các công thức sau, công thức nào đúng?
|
A. \(\sin \left( {a-b} \right) = \sin a.\cos b - \cos a.\sin b.\). |
B. \(\cos \left( {a-b} \right) = \cos a.\cos b - \sin a.\sin b.\). |
|
C. \(\sin \left( {a + b} \right) = \sin a.\cos b - \cos a.\sin b.\). |
D. \(\cos \left( {a + b} \right) = \cos a.\cos b + \sin a.\sin b.\). |
Phương pháp
Sử dụng công thức cộng.
Lời giải
Ta có: \(\sin \left( {a-b} \right) = \sin a.\cos b - \cos a.\sin b.\).
Đáp án A
Câu 4: Mệnh đề nào sau đây đúng?
|
A. \(\cos 2a = {\cos ^2}a - {\sin ^2}a\) |
B. \(\cos 2a = {\cos ^2}a + {\sin ^2}a\) |
|
C. \(\cos 2a = 2{\cos ^2}a + 1\) |
D. \(\cos 2a = 2{\sin ^2}a - 1\) |
Phương pháp
Áp dụng công thức nhân đôi
Lời giải
Ta có: \(\cos 2a = {\cos ^2}a - {\sin ^2}a = 2{\cos ^2}a - 1 = 1 - 2{\sin ^2}a\).
Đáp án A
Câu 5: Hàm số nào sau đây là hàm số chẵn?
|
A. \(y = - 2\cos x\) |
B. \(y = - 2\sin x\) |
|
C. \(y = 2\sin \left( { - x} \right)\) |
D. \(y = \sin x - \cos x\) |
Phương pháp
Để xét tính chẵn – lẻ của hàm số, ta làm như sau:
Bước 1: Tìm tập xác định \(D\) của hàm số, khi đó:
- Nếu \(D\) là tập đối xứng (tức \(\forall x \in D \Rightarrow - x \in D\)), thì ta thực hiện tiếp bước 2.
- Nếu \(D\) không phải tập đối xứng (tức là \(\exists x \in D\) mà \( - x \notin D\)) thì ta kết luận hàm số không chẵn không lẻ.
Bước 2: Xác định \(f\left( { - x} \right)\):
- Nếu \(f\left( { - x} \right) = f\left( x \right),\forall x \in D\) thì kết luận hàm số là hàm số chẵn.
- Nếu \(f\left( { - x} \right) = - f\left( x \right),\forall x \in D\) thì kết luận hàm số là hàm số lẻ.
- Nếu không thỏa mãn một trong hai điều kiện trên thì kết luận hàm số không chẵn không lẻ.
Lời giải
Xét đáp án A:
Do tập xác định \(D = \mathbb{R}\) nên \(\forall x \in \mathbb{R} \Rightarrow - x \in \mathbb{R}\).
Ta có: \(f\left( { - x} \right) = - 2\cos \left( { - x} \right) = - 2\cos x = f\left( x \right)\).
Vậy hàm số \(y = - 2\cos x\) là hàm số chẵn.
Đáp án A
Câu 6: Hình nào dưới đây biểu diễn đồ thị hàm số \(y = f(x) = 2\sin 2x?\)
|
A. |
B. |
|
C. |
D. |
Phương pháp
Dựa vào các điểm đặc biết của đồ thị để nhận biết hàm số.
Lời giải
Ta thấy \( - 2 \le 2\sin 2x \le 2\) nên ta có loại A và B.
Tiếp theo với C và D ta có :
Ta thấy với \(x = 0\) thì \(y = 0\) nên đồ thị hàm số đi qua gốc tọa độ.
Từ đây ta chọn đáp án C.
Đáp án C
Câu 7: Nghiệm của phương trình \(\cos x = \frac{1}{2}\) là:
|
A. \(x = \pm \frac{\pi }{2} + k2\pi \) |
B. \(x = \pm \frac{\pi }{3} + k2\pi \) |
|
C. \(x = \pm \frac{\pi }{4} + k2\pi \) |
D. \(x = \pm \frac{\pi }{6} + k2\pi \) |
Phương pháp
- Trường hợp \(\left| m \right| > 1\) phương trình vô nghiệm.
- Trường hợp \(\left| m \right| \le 1\), khi đó: Tồn tại duy nhất một số thực \(\alpha \in \left[ { - \frac{\pi }{2};\frac{\pi }{2}} \right]\) sao cho \(\cos \alpha = m\).
Ta có : \(\cos x = \cos \alpha \Leftrightarrow \left[ \begin{array}{l}x = \alpha + k2\pi \\x = - \alpha + k2\pi \end{array} \right.,\left( {k \in \mathbb{Z}} \right)\).
Lời giải
Ta có: \(\cos x = \frac{1}{2} \Leftrightarrow \cos x = \cos \frac{\pi }{3} \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{x = \frac{\pi }{3} + k2\pi }\\{x = - \frac{\pi }{3} + k2\pi }\end{array}} \right.\left( {k \in \mathbb{Z}} \right)\)
Đáp án B
Câu 8: Trên đoạn \(\left[ {0;2018\pi } \right]\), phương trình \(\sqrt 3 \cot x - 3 = 0\) có số nghiệm là :
|
A. \(2018.\) |
B. \(6340.\) |
|
C. \(2017.\) |
D. \(6339.\) |
Phương pháp
Áp dụng các công thức giải phương trình lượng giác cơ bản rồi kết hợp điều kiện đã cho để chọn nghiệm thỏa mãn.
Lời giải
Ta có : \(\cot x = \sqrt 3 \Leftrightarrow \cot x = \cot \frac{\pi }{6} \Leftrightarrow x = \frac{\pi }{6} + k\pi {\rm{ }}\left( {k \in \mathbb{Z}} \right).\)
Theo giả thiết, ta có $0\le \frac{\pi }{6}+k\pi \le 2018\pi \xrightarrow{\text{xap xi}}-\frac{1}{6}\le k\le 2017,833$.
$3\xrightarrow{k\in \mathbb{Z}}k\in \left\{ 0;1;...;2017 \right\}$.
Vậy có tất cả \(2018\) giá trị nguyên của \(k\) tương ứng với có \(2018\) nghiệm thỏa mãn yêu cầu bài toán.
Đáp án A
Câu 9: Cho dãy số có các số hạng đầu là: \(\frac{1}{3};\,\frac{1}{{{3^2}}};\,\frac{1}{{{3^3}}};\,\frac{1}{{{3^4}}};\,\frac{1}{{{3^5}}};\,...\)Số hạng tổng quát của dãy số này là?
|
A. \({u_n} = \frac{1}{3}.\frac{1}{{{3^{n + 1}}}}\) |
B. \({u_n} = \frac{1}{{{3^{n + 1}}}}\) |
|
C. \({u_n} = \frac{1}{{{3^n}}}\) |
D. \({u_n} = \frac{1}{{{3^{n - 1}}}}\) |
Phương pháp
Tìm tính chất chung của các số trong dãy số rồi dự đoán công thức tổng quát.
Lời giải
Từ các số hạng đầu tiên của dãy số ta dự đoán \({u_n} = \frac{1}{{{3^n}}},\,n \in {\mathbb{N}^*}\).
Đáp án C
Câu 10: Cho dãy số \(\left( {{u_n}} \right)\) xác định bởi \(\left\{ \begin{array}{l}{u_1} = 2\\{u_{n + 1}} = \frac{1}{3}\left( {{u_n} + 1} \right)\end{array} \right..\) Tìm số hạng \({u_4}.\)
|
A. \({u_4} = \frac{5}{9}.\) |
B. \({u_4} = 1.\) |
|
C. \({u_4} = \frac{2}{3}.\) |
D. \({u_4} = \frac{{14}}{{27}}.\) |
Phương pháp
Tính lần lượt \({u_2},{u_3},{u_4}\) theo bằng cách thay lần lượt \(n = 1,2,3\) vào công thức truy hồi của dãy số.
Lời giải
Ta có:
\({u_2} = \frac{1}{3}\left( {{u_1} + 1} \right) = \frac{1}{3}\left( {2 + 1} \right) = 1\).
\({u_3} = \frac{1}{3}\left( {{u_2} + 1} \right) = \frac{1}{3}\left( {1 + 1} \right) = \frac{2}{3}\).
\({u_4} = \frac{1}{3}\left( {{u_3} + 1} \right) = \frac{1}{3}\left( {\frac{2}{3} + 1} \right) = \frac{5}{9}\).
Vậy \({u_4} = \frac{5}{9}\).
Đáp án A
Câu 11: Trong các dãy số sau đây, dãy số nào là cấp số cộng?
|
A. \({u_n} = {3^n}\) |
B. \({u_n} = {\left( { - 3} \right)^{n + 1}}\) |
|
C. \({u_n} = 3n + 1\) |
D. \({u_n} = {2^{n + 1}}\) |
Phương pháp
Để chứng minh dãy số \(\left( {{u_n}} \right)\) là một cấp số cộng, ta xét \(A = {u_{n + 1}} - {u_n}\)
\( \bullet \) Nếu \(A\) là hằng số thì \(\left( {{u_n}} \right)\) là một cấp số cộng với công sai \(d = A\).
\( \bullet \) Nếu \(A\) phụ thuộc vào \(n\) thì \(\left( {{u_n}} \right)\) không là cấp số cộng.
Lời giải
Ta có:
Xét đáp án A: \({u_{n + 1}} - {u_n} = {3^{n + 1}} - {3^n} = {2.3^n}\left( {\forall n \in {{\rm N}^*}} \right)\) nên \({u_n} = {3^n}\) không phải là cấp số cộng.
Xét đáp án B: \({u_{n + 1}} - {u_n} = {\left( { - 3} \right)^{n + 1}} - {\left( { - 3} \right)^n} = - 4.{\left( { - 3} \right)^n}\left( {\forall n \in {{\rm N}^*}} \right)\) nên \({u_n} = {\left( { - 3} \right)^{n + 1}}\) không phải là cấp số cộng.
Xét đáp án C: \({u_{n + 1}} - {u_n} = \left[ {3\left( {n + 1} \right) + 1} \right] - \left( {3n + 1} \right) = 3\left( {\forall n \in {{\rm N}^*}} \right)\) không đổi, nên \({u_n} = 3n + 1\) là cấp số cộng.
Xét đáp án D: \({u_{n + 1}} - {u_n} = {2^{n + 2}} - {2^{n + 1}} = {2^{n + 1}}\left( {\forall n \in {{\rm N}^*}} \right)\) nên \({u_n} = {2^{n + 1}}\) không phải là cấp số cộng.
Đáp án C
Câu 12: Cho cấp số cộng \(\left( {{u_n}} \right)\) và gọi \({S_n}\) là tổng \(n\) số hạng đầu tiên của nó. Biết \({u_{21}} = - 19\) và \({S_{22}} = 0\). Tìm số hạng tổng quát \({u_n}\) của cấp số cộng đó.
|
A. \({u_n} = 21 + 2n\) |
B. \({u_n} = 21 - 2n\) |
|
C. \({u_n} = 23 - 2n\) |
D. \({u_n} = 23 + 2n\) |
Phương pháp
Dựa vào giả thuyết, ta lập một hệ phương trình chứa công sai d và số hạng đầu \({u_1}\), giải hệ phương trình này tìm được d và \({u_1}\).
Lời giải
Giả sử cấp số cộng có số hạng đầu là \({u_1}\) và công sai \(d\).
Ta có: \(\left\{ \begin{array}{l}{u_{21}} = - 19\\{S_{22}} = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{u_{21}} = {u_1} + 20d\\{S_{22}} = 22{u_1} + \frac{{22.21d}}{2}\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{u_1} + 20d = - 19\\2{u_1} + 21d = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{u_1} = 21\\d = - 2\end{array} \right.\).
Khi đó: \({u_n} = {u_1} + \left( {n - 1} \right)d = 21 - 2\left( {n - 1} \right) = 23 - 2n\).
Đáp án C
Câu 13: Hùng đang tiết kiệm để mua một cây đàn piano có giá 142 triệu đồng. Trong tháng đầu tiên, anh ta để dành được 20 triệu đồng. Mỗi tháng tiếp theo anh ta để dành được 3 triệu đồng và đưa số tiền tiết kiệm của mình. Hỏi ít nhất vào tháng thứ bao nhiêu thì Hùng mới có đủ tiền để mua cây đàn piano đó?
|
A. \(43\) |
B. \(41\) |
|
C. \(40\) |
D. \(42\) |
Phương pháp
Cho một cấp số cộng \(\left( {{u_n}} \right)\) có số hạng đầu \({u_1}\) và công sai \(d\).
Khi đó : \({u_n} = {u_1} + \left( {n - 1} \right)d\)
Lời giải
Tổng số tiền Hùng tiết kiệm được vào mỗi tháng lập thành một cấp số cộng \(\left( {{u_n}} \right)\) có số hạng đầu \({u_1} = 20\) và công sai \(d = 3\).
Tổng số tiền Hùng tiết kiệm được vào tháng thứ \(n\) bằng: \({u_n} = {u_1} + \left( {n - 1} \right)d = 20 + \left( {n - 1} \right).3 = 3n + 17\).
Hùng có đủ tiền mua cây đàn \({u_n} \ge 142 \Leftrightarrow 3n + 17 \ge 142\) \( \Leftrightarrow n \ge \frac{{125}}{3} \approx 41,67\).
Vậy ít nhất vào tháng thứ 42 thì Hùng mới có đủ tiền để mua cây đàn piano đó.
Đáp án D
Câu 14: Trong các dãy số cho dưới đây, dãy số nào là cấp số nhân?
|
A. \(1;\,2;\,3;\,4;\,5\) |
B. \(1;\,3;\,6;\,9;\,12\) |
|
C. \(2;\,4;\,6;\,8;\,10\) |
D. \(2;\,2;\,2;\,2;\,2\) |
Phương pháp
Chứng minh \(\forall n \ge 1,{u_{n + 1}} = {u_n}.q\) trong đó \(q\) là một số không đổi.
Nếu \({u_n} \ne 0\) với mọi \(n \in {\mathbb{N}^*}\) thì ta lập tỉ số \(T = \frac{{{u_{n + 1}}}}{{{u_n}}}\).
\( * \) T là hằng số thì \(({u_n})\) là cấp số nhân có công bội \(q = T\).
\( * \) T phụ thuộc vào n thì \(({u_n})\) không là cấp số nhân.
Lời giải
Ta thấy ở đáp án D có \({u_1} = {u_2} = {u_3} = {u_4} = {u_5} = 2\) nên đây là cấp số nhân với công bội \(q = 1\).
Đáp án D
Câu 15: Cho cấp số nhân \(\left( {{u_n}} \right)\) có số hạng đầu \({u_1} = 2\) và \({u_6} = 486\). Công bội q bằng
|
A. \(q = 3\) |
B. \(q = 5\) |
|
C. \(q = \frac{3}{2}\) |
D. \(q = \frac{2}{3}\) |
Phương pháp
Dựa vào giả thuyết, ta lập một hệ phương trình chứa công bội q và số hạng đầu \({u_1}\), giải hệ phương trình này tìm được q và \({u_1}\).
Lời giải
Theo đề ra ta có: \(\left\{ \begin{array}{l}{u_1} = 2\\{u_6} = 486\end{array} \right.\) \( \Leftrightarrow \left\{ \begin{array}{l}{u_1} = 2\\486 = {u_1}.{q^5}\end{array} \right.\)\( \Rightarrow {q^5} = 243 = {3^5}\)\( \Rightarrow q = 3\).
Đáp án A
Câu 16: Cho \(\left( {{u_n}} \right)\) là cấp số nhân, đặt \({S_n} = {u_1} + {u_2} + ... + {u_n}\). Biết \({S_2} = 4;\,{S_3} = 13\)và \({u_2} < 0\), giá trị \({S_5}\) bằng
|
A. \(2\) |
B. \(\frac{{181}}{{16}}\) |
|
C. \(\frac{{35}}{{16}}\) |
D. \(121\) |
Phương pháp
Cho một cấp số cộng \(\left( {{u_n}} \right)\) có số hạng đầu \({u_1}\) và công bội \(q\).
Đặt \({S_n} = {u_1} + {u_2} + ... + {u_n}\).
Khi đó : \({S_n} = {u_1}.\frac{{1 - {q^n}}}{{1 - q}},q \ne 1\).
Lời giải
Gọi \({u_1},q\) lần lượt là số hạng đầu tiên và công bội của cấp số nhân cần tìm.
Từ giả thiết ta có \(\left\{ \begin{array}{l}{S_2} = 4\\{S_3} = 13\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{u_1}\left( {1 + q} \right) = 4\\{u_1}\left( {1 + q + {q^2}} \right) = 13\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{u_1}\left( {1 + q} \right) = 4\\\left[ \begin{array}{l}q = 3\\q = \frac{{ - 3}}{4}\end{array} \right.\end{array} \right.\).
Vì \(\left\{ \begin{array}{l}{u_2} < 0\\{u_3} = {S_3} - {S_2} = 9 > 0\end{array} \right. \Rightarrow q = \frac{{{u_3}}}{{{u_2}}} < 0\) nên cấp số nhân cần tìm có \(\left\{ \begin{array}{l}{u_1} = 16\\q = - \frac{3}{4}\end{array} \right.\).
Do đó \({S_5} = {u_1}\left( {\frac{{1 - {q^5}}}{{1 - q}}} \right) = \frac{{181}}{{16}}\).
Đáp án B
Câu 17: Cho mẫu số liệu ghép nhóm về thời gian (phút) đi từ nhà đến nơi làm việc của các nhân viên một công ty như sau:
|
Thời gian |
\(\left[ {15;20} \right)\) |
\(\left[ {20;25} \right)\) |
\(\left[ {25;30} \right)\) |
\(\left[ {30;35} \right)\) |
\(\left[ {35;40} \right)\) |
\(\left[ {40;45} \right)\) |
\(\left[ {45;50} \right)\) |
|
Số nhân viên |
6 |
14 |
25 |
37 |
21 |
13 |
9 |
Có bao nhiêu nhân viên có thời gian đi từ nhà đến nơi làm việc là từ 15 phút đến dưới 20 phút?
|
A. 6 |
B. \(9\) |
|
C. 14 |
D. 13 |
Phương pháp
Đọc bảng số liệu.
Lời giải
Có 6 nhân viên có thời gian đi từ nhà đến nơi làm việc là từ 15 phút đến dưới 20 phút.
Đáp án A
Câu 18: Cho mẫu số liệu ghép nhóm sau:
|
Nhóm |
\(\left[ {{a_1};{a_2}} \right)\) |
. |
\(\left[ {{a_i};{a_{i + 1}}} \right)\) |
. |
\(\left[ {{a_k};{a_{k + 1}}} \right)\) |
|
Tần số |
\({m_1}\) |
. |
\({m_i}\) |
. |
\({m_k}\) |
Với \(n = {m_1} + {m_2} + ... + {m_k}\) là cỡ mẫu và \({x_i} = \frac{{{a_i} + {a_{i + 1}}}}{2}\) (\(i = 1,...k\)) là giá trị đại diện của nhóm \(\left[ {{a_i};{a_{i + 1}}} \right)\). Khi đó công thức tính số trung bình cộng của mẫu số liệu ghép nhóm trên là:
|
A. \(\bar x = \frac{n}{{{m_1}{x_1} + \ldots + {m_k}{x_k}}}\) |
B. \(\bar x = \frac{{\left( {{m_1}{x_1}} \right) \ldots \left( {{m_k}{x_k}} \right)}}{n}\) |
|
C. \(\bar x = \frac{{{m_1}{x_1} - \ldots - {m_k}{x_k}}}{n}\) |
D. \(\bar x = \frac{{{m_1}{x_1} + \ldots + {m_k}{x_k}}}{n}\) |
Phương pháp
Số trung bình của mẫu số liệu ghép nhóm kí hiệu là \(\bar x\).
\(\bar x = \frac{{{m_1}{x_1} + \ldots + {m_k}{x_k}}}{n}\)
trong đó, \(n = {m_1} + \ldots + {m_k}\) là cỡ mẫu và \({x_i} = \frac{{{a_i} + {a_{i + 1}}}}{2}\) (với \(i = 1, \ldots ,k\) ) là giá trị đại diện của nhóm \(\left[ {{a_i};{a_{i + 1}}} \right)\).
Lời giải
Số trung bình của mẫu số liệu ghép nhóm kí hiệu là \(\bar x\).
\(\bar x = \frac{{{m_1}{x_1} + \ldots + {m_k}{x_k}}}{n}\)
Đáp án D
Câu 19: Thời gian luyện tập trong một ngày (tính theo giờ) của một số vận động viên được ghi lại ở bảng sau:

Tứ phân vị thứ ba của mẫu số liệu trên gần nhất với giá trị nào trong các giá trị sau?
|
A. 3 |
B. 4 |
|
C. 7 |
D. 5 |
Phương pháp
Để tính tứ phân vị thứ nhất \({Q_3}\) của mẫu số liệu ghép nhóm, trước hết ta xác định nhóm chứa \({Q_3}\), giả sử đó là nhóm thứ \(p\) : \(\left[ {{a_p};{a_{p + 1}}} \right)\). Khi đó,
\({Q_3} = {a_p} + \frac{{\frac{{3n}}{4} - \left( {{m_1} + \ldots + {m_{p - 1}}} \right)}}{{{m_p}}} \cdot \left( {{a_{p + 1}} - {a_p}} \right),\)
trong đó, \(n\) là cỡ mẫu, \({m_p}\) là tần số nhóm \(p\), với \(p = 1\) ta quy ước \({m_1} + \ldots + {m_{p - 1}} = 0\).
Lời giải
Tứ phân vị thứ ba của dãy số liệu \({x_1};{x_2}, \ldots ,{x_{39}}\) là \({x_{30}} \in \left[ {6;8} \right)\). Do đó tứ phân vị thứ ba của mẫu số liệu ghép nhóm là
\({Q_3} = 6 + \frac{{\frac{{3.39}}{4} - \left( {3 + 8 + 12} \right)}}{{12}} \cdot \left( {8 - 6} \right) = \frac{{169}}{{24}} \approx 7,042\)
Đáp án C
Câu 20: Trong một hội thao, thời gian chạy \(200{\rm{\;m}}\) của một nhóm các vận động viên được ghi lại ở bảng sau:

Trung vị của mẫu số liệu ghép nhóm trên thuộc khoảng nào trong các khoảng dưới đây?
|
A. \(\left[ {20;30} \right)\) |
B. \(\left[ {30;40} \right)\) |
|
C. \(\left[ {50;60} \right)\) |
D. \(\left[ {60;70} \right)\) |
Phương pháp
- Gọi\(n\) là cỡ mẫu.
- Giả sử nhóm \(\left[ {{u_m};{u_{m + 1}}} \right)\) chứa trung vị;
- \({n_m}\) là tần số của nhóm chứa trung vị;
- \(C = {n_1} + {n_2} + \ldots + {n_{m - 1}}\).
Khi đó \({M_e} = {u_m} + \frac{{\frac{n}{2} - C}}{{{n_m}}} \cdot \left( {{u_{m + 1}} - {u_m}} \right)\)
Lời giải
Số vận động viên tham gia chạy là: \(n = 5 + 12 + 32 + 45 + 30 = 124\)
Gọi \({x_1};{x_2};{x_3}; \ldots ;{x_{124}}\) lần lượt là thời gian chạy của các vận động viên theo thứ tự từ nhỏ đến lớn
Do \({x_1}, \ldots ,{x_5} \in \left[ {21;21,5} \right);{x_6}, \ldots ,{x_{17}} \in \left[ {21,5;22} \right)\)
\({x_{18}}, \ldots ,{x_{49}} \in \left[ {22;22,5} \right);{x_{50}}, \ldots ,{x_{94}} \in \left[ {22,5;23} \right); \ldots \) nên trung vị của mẫu số liệu thuộc nhóm \(\left[ {22,5;23} \right)\)
Ta có: \(n = 124;{n_m} = 45;C = 5 + 12 + 32 = 49;{u_m} = 22,5;{u_{m + 1}} = 23\)
Trung vị của mẫu số liệu ghép nhóm là:
\({M_e} = 22,5 + \frac{{\frac{{124}}{2} - 49}}{{124}} \cdot \left( {23 - 22,5} \right) = 22,55\)
Đáp án A
Phần tự luận.
Bài 1.
Tìm giá trị lớn nhất và giá trị nhỏ nhất : \(y = {\tan ^2}x - \tan x + 1\) với \(x \in \left[ { - \frac{\pi }{4};\,\frac{\pi }{4}} \right]\).
Phương pháp
B1: Đặt ẩn phụ và tìm điều kiện của ẩn
B2: Lập bảng biến thiên, khảo sát hàm số rồi kết luận
Lời giải
Đặt \(tanx = t\), \(t \in \left[ { - 1\,;\,1} \right]\), hàm số có dạng: \(y = {t^2} - t + 1\).
Xét hàm số \(y = {t^2} - t + 1\) trên \(\left[ { - 1\,;\,1} \right]\) có BBT như sau:
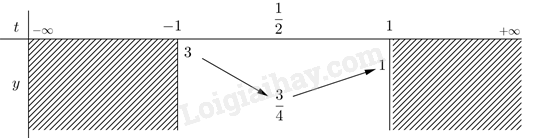
Giá trị nhỏ nhất của hàm số bằng \(\frac{3}{4}\) khi và chỉ khi \(t = \frac{1}{2}\) tức \(tanx = \frac{1}{2}\)\( \Leftrightarrow \)\(x = \arctan \left( {\frac{1}{2}} \right) + k\pi \), \(k \in \mathbb{Z}\).
Giá trị lớn nhất của hàm số bằng \(3\) khi và chỉ khi \(t = - 1\) tức là \(tanx = - 1\)\( \Leftrightarrow \)\(x = - \frac{\pi }{4} + k\pi \), \(k \in \mathbb{Z}\).
Bài 2.
a) Giải phương trình \(\cot \;x = \sqrt 3 \)
b) Trong khoảng \(\left( {0;\pi } \right)\), phương trình \(\cos 4x + \sin x = 0\) có tập nghiệm là \(S\). Tìm S.
c) Giải phương trình \(\frac{3}{2} - 3cos4x = 6sinx.sin3x\).
Phương pháp
a) Ta có: \(\cot x = m\,\)\( \Leftrightarrow \cot x = \cot \alpha \Leftrightarrow x = \alpha + k\pi \,\,\left( {k \in \mathbb{Z}} \right)\).
b) Áp dụng các công thức giải phương trình lượng giác cơ bản rồi kết hợp điều kiện đã cho để chọn nghiệm thỏa mãn.
c) Sử dụng công thức biến tích thành tổng để rút gọn phương trình: \(\sin a.\sin b = \frac{1}{2}\left[ {\cos \left( {a - b} \right) - \cos \left( {a + b} \right)} \right]\).
Lời giải
a) Ta có: \(\cot x = \sqrt 3 \)\( \Leftrightarrow \cot x = \cot \;\frac{\pi }{6}\)\( \Leftrightarrow x = \frac{\pi }{6} + k\pi \;\;\left( {k \in \mathbb{Z}} \right)\)\( \Leftrightarrow x = \frac{{ - 5\pi }}{6} + k\pi \;\;\left( {k \in \mathbb{Z}} \right)\).
b) Ta có \(\cos 4x + \sin x = 0 \Leftrightarrow {\rm{cos}}4x = - \sin x \Leftrightarrow {\rm{cos}}4x = \sin \left( { - x} \right) \Leftrightarrow {\rm{cos}}4x = {\rm{cos}}\left( {\frac{\pi }{2} + x} \right)\)
\( \Leftrightarrow \left[ \begin{array}{l}4x = \frac{\pi }{2} + x + k2\pi \\4x = - \frac{\pi }{2} - x + k2\pi \end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = \frac{\pi }{6} + k\frac{{2\pi }}{3}\\x = - \frac{\pi }{{10}} + k\frac{{2\pi }}{5}\end{array} \right.\), \(k \in \mathbb{Z}\).
Vì \(x \in \left( {0;\pi } \right)\) nên \(S = \left\{ {\frac{\pi }{6};\frac{{5\pi }}{6};\frac{{3\pi }}{{10}};\frac{{7\pi }}{{10}}} \right\}\).
c) Ta có: \(\frac{3}{2} - 3cos4x = 6sinx.sin3x\)
\( \Leftrightarrow \frac{3}{2} - 3\cos 4x = 3(\cos 2x - \cos 4x)\)
\( \Leftrightarrow 3\cos 2x = \frac{3}{2}\)
\(\begin{array}{l} \Leftrightarrow \cos 2x = \frac{1}{2}\,\\ \Leftrightarrow {\mathop{\rm x}\nolimits} = \pm \frac{\pi }{6} + {\mathop{\rm k}\nolimits} \pi ,{\mathop{\rm k}\nolimits} \in \mathbb{Z}\,\end{array}\).
Bài 3.
a) Một cơ sở khoan giếng đưa ra định mức giá như sau : Giá từ mét khoan đầu tiên là \(100000\) đồng và kể từ mét khoan thứ hai, giá mỗi mét tăng thêm \(30000\) đồng so với giá của mét khoan ngay trước đó. Một người muốn kí hợp đồng với cơ sở khoan giếng này để khoan giếng sâu \(20\) mét lấy nước dùng cho sinh hoạt gia đình. Hỏi sau khi hoàn thành việc khoan giếng, gia đình đó phải thanh toán cho cơ sở khoan giếng số tiền bằng bao nhiêu?
b) Cho cấp số nhân \(\left( {{x_n}} \right)\) có \({x_2} = - 3\) và \({x_4} = - 27.\) Tính số hạng đầu \({x_1}\) và công bội \(q\) của cấp số nhân
Phương pháp
a) Cho một cấp số cộng \(\left( {{u_n}} \right)\) có số hạng đầu \({u_1}\) và công sai \(d\).
Đặt \({S_n} = {u_1} + {u_2} + ... + {u_n}\).
Khi đó : \({S_n} = \frac{{n\left( {{u_1} + {u_n}} \right)}}{2}\) hoặc \({S_n} = \frac{{n\left[ {2{u_1} + (n - 1)d} \right]}}{2} = n{u_1} + \frac{{n\left( {n - 1} \right)}}{2}d\) .
b) Dựa vào giả thuyết, ta lập một hệ phương trình chứa công bội q và số hạng đầu \({u_1}\), giải hệ phương trình này tìm được q và \({u_1}\).
Lời giải
a) Giá tiền mỗi mét khoan giếng lập thành một cấp số cộng với
\({u_1} = 100000\) (số tiền mét khoan đầu tiên),
\({u_2} = {u_1} + 30000\) (số tiền mét khoan thứ hai),
\({u_3} = {u_2} + 30000 = {u_1} + 2.30000\) (số tiền mét khoan thứ ba)
…
\({u_{20}} = {u_{19}} + 30000 = {u_1} + 19.30000\) (số tiền mét khoan thứ 20),
và công sai \(d = 30000\).
Tổng chi phí cần phải thanh toán là:
\({S_{20}} = {u_1} + {u_2} + {u_3} + ... + {u_{20}}\) \( = \frac{{20(2.10000 + 19.30000)}}{2}\)\( = 7700000\).
b) Ta có : \(\left\{ {\begin{array}{*{20}{c}}{{x_2} = - 3}\\{{x_4} = - 27.}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{{x_1}q = - 3}\\{{x_1}{q^3} = - 27.}\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{{q^2} = 9}\\{{x_1} = - \frac{3}{q}.}\end{array}} \right.} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{q = \pm 3}\\{{x_1} = \mp 1.}\end{array}} \right.\).
Vậy dãy số có \({x_1} = - 1,q = 3\) hoặc \({x_1} = 1,q = - 3.\)
Bài 4.
Một người thống kê lại thời gian thực hiện các cuộc gọi điện thoại của người đó trong một tuần ở bảng sau:

a) Tính trung vị của mẫu số liệu ghép nhóm này.
b) Tìm tứ phân vị thứ nhất và tứ phân vị thứ ba của mẫu số liệu ghép nhóm này.
Phương pháp
a) Để tính trung vị của mẫu số liệu ghép nhóm, ta làm như sau:
Bước 1. Xác định nhóm chứa trung vị. Giả sử đó là nhóm thứ \(p\) : \(\left[ {{a_p};{a_{p + 1}}} \right)\).
Bước 2. Trung vị là \({M_e} = {a_p} + \frac{{\frac{n}{2} - \left( {{m_1} + \ldots + {m_{p - 1}}} \right)}}{{{m_p}}} \cdot \left( {{a_{p + 1}} - {a_p}} \right)\),
trong đó \(n\) là cỡ mẫu, \({m_p}\) là tần số nhóm \(p\). Với \(p = 1\), ta quy ước \({m_1} + \ldots + {m_{p - 1}} = 0\).
b) Để tính tứ phân vị thứ nhất \({Q_1}\) của mẫu số liệu ghép nhóm, trước hết ta xác định nhóm chứa \({Q_1}\), giả sử đó là nhóm thứ \(p\) : \(\left[ {{a_p};{a_{p + 1}}} \right)\). Khi đó,
\({Q_1} = {a_p} + \frac{{\frac{n}{4} - \left( {{m_1} + \ldots + {m_{p - 1}}} \right)}}{{{m_p}}} \cdot \left( {{a_{p + 1}} - {a_p}} \right),\)
trong đó, \(n\) là cỡ mẫu, \({m_p}\) là tần số nhóm \(p\), với \(p = 1\) ta quy ước \({m_1} + \ldots + {m_{p - 1}} = 0\).
Để tịnh tứ phân vị thứ ba \({Q_3}\) của mẫu số liệu ghép nhóm, trước hết ta xác định nhóm chứa \({Q_3}\). Giả sử đó là nhóm thứ \(p\) : \(\left[ {{a_p};{a_{p + 1}}} \right)\). Khi đó,
\({Q_3} = {a_p} + \frac{{\frac{{3n}}{4} - \left( {{m_1} + \ldots + {m_{p - 1}}} \right)}}{{{m_p}}} \cdot \left( {{a_{p + 1}} - {a_p}} \right),\)
trong đó, \(n\) là cỡ mẫu, \({m_p}\) là tần số nhóm \(p\), với \(p = 1\) ta quy ước \({m_1} + \ldots + {m_{p - 1}} = 0\).
Tứ phân vị thứ hai \({Q_2}\) chính là trung vị \({M_e}\).
Nhận xét. Ta cũng có thể xác định nhóm chứa tứ phân vi thứ \(r\) nhờ tính chất: có khoảng \(\left( {\frac{{r \cdot n}}{4}} \right)\) giá trị nhỏ hơn tứ phân vị này.
Lời giải
a) Số lần thực hiện cuộc gọi là: \({\rm{n}} = 8 + 10 + 7 + 5 + 2 + 1 = 33\).
Gọi \({x_1};{x_2};{x_3}; \ldots ;{x_{33}}\) lần lượt là thời gian thực hiện cuộc gọi theo thứ tự không gian.
Do \({x_1}, \ldots ,{x_8} \in \left[ {0;60} \right);{x_9}, \ldots ,{x_{18}} \in \left[ {60;120} \right);{x_{19}}, \ldots ,{x_{25}} \in \left[ {120;180} \right)\) \({x_{26}}, \ldots ,{x_{30}} \in \left[ {180;240} \right); \ldots \)
Trung vị của dãy số liệu là \(\frac{1}{2}\left( {{x_{16}} + {x_{17}}} \right)\) thuộc nhóm \(\left[ {60;120} \right)\)nên tứ phân vị thứ hai của mẫu số liệu là
\({Q_2} = 60 + \frac{{\frac{{33}}{2} - 8}}{{10}}\left( {120 - 60} \right) = 111\).
b) Tứ phân vị thứ hai của dãy số liệu là \(\frac{1}{2}\left( {{x_{16}} + {x_{17}}} \right)\) thuộc nhóm \(\left[ {60;120} \right)\)nên tứ phân vị thứ hai của mẫu số liệu là \({Q_2} = 60 + \frac{{\frac{{33}}{2} - 8}}{{10}}\left( {120 - 60} \right) = 111\).
Tứ phân vị thứ ba của dãy số liệu là \(\frac{1}{2}\left( {{x_{24}} + {x_{25}}} \right)\) thuộc nhóm [120;180) nên tứ phân vị thứ ba của mẫu số liệu là \({Q_3} = 120 + \frac{{\frac{{3.33}}{4} - 18}}{7}\left( {180 - 120} \right) = 177,8\).
- Đề thi giữa kì 1 Toán 11 Kết nối tri thức - Đề số 4
- Đề thi giữa kì 1 Toán 11 Kết nối tri thức - Đề số 5
- Đề thi giữa kì 1 Toán 11 Kết nối tri thức - Đề số 6
- Đề thi giữa kì 1 Toán 11 Kết nối tri thức - Đề số 7
- Đề thi giữa kì 1 Toán 11 Kết nối tri thức - Đề số 8
>> Xem thêm
Luyện Bài Tập Trắc nghiệm Toán 11 - Kết nối tri thức - Xem ngay














Danh sách bình luận