Đề thi, đề kiểm tra Toán lớp 7 - Chân trời sáng tạo Đề thi giữa kì 2 Toán 7 Chân trời sáng tạo

Đề thi giữa kì 2 Toán 7 Chân trời sáng tạo - Đề số 7

Tải về

Tổng hợp đề thi học kì 1 lớp 7 tất cả các môn - Chân trời sáng tạo

Toán - Văn - Anh - Khoa học tự nhiên...

Phần trắc nghiệm (3 điểm) Câu 1: Nếu 4.b = 5.c và b, c ≠ 0 thì:

Đề bài

Xem đáp án

Làm đề thi

Tải về

Đề bài

I. Trắc nghiệm

Câu 1 :

Nếu 4.b = 5.c và b, c ≠ 0 thì:

A.
$\frac{4}{c} = \frac{b}{5}$.
B.
$\frac{b}{5} = \frac{c}{4}$.
C.
$\frac{4}{b} = \frac{5}{c}$.
D.
$\frac{c}{5} = \frac{b}{4}$.

Câu 2 :

Nếu các số x, y, z tỉ lệ với các số 6; 4; 3 thì ta có dãy tỉ số bằng nhau nào:

A.
$\frac{x}{4} = \frac{y}{3} = \frac{z}{6}$.
B.
$\frac{3}{x} = \frac{4}{y} = \frac{6}{z}$.
C.
$\frac{x}{3} = \frac{y}{4} = \frac{z}{6}$.
D.
$\frac{x}{6} = \frac{y}{4} = \frac{z}{3}$.

Câu 3 :

Đại lượng y tỉ lệ thuận với đại lượng x theo hệ số tỉ lệ 5. Ta có:

A.
y = 5.x.
B.
$y = \frac{1}{5}.x$.
C.
y = x.
D.
y = x + 5.

Câu 4 :

Cho x và y là hai đại lượng tỉ lệ thuận với nhau. Biết hệ số tỉ lệ của x đối với y là 8. Hệ số tỉ lệ của y đối với x là:

A.
5.
B.
8.
C.
$\frac{1}{8}$.
D.
5.

Câu 5 :

Cho biết y và x là hai đại lượng tỉ lệ nghịch theo hệ số tỉ lệ a. Ta có:

A.
y = ax.
B.
$y = \frac{a}{x}$.
C.
$x = \frac{y}{a}$.
D.
$y = a - x$.

Câu 6 :

Cho tam giác ABC. Trong các khẳng định sau khẳng định nào sai?

A.
$AB + AC > BC$.
B.
$AB + BC > AC$.
C.
$AC - BC > AB$.
D.
$AB < AC + BC$.

Câu 7 :

Cho $\Delta ABC = \Delta DEF$. Khi đó:

A.
AB = DE.
B.
AC = DE.
C.
BC = DF.
D.
BC = DE.

Câu 8 :

Cho $\Delta ABC = \Delta DEF$, $\hat C = {40^0}$. Khi đó:

A.
$\hat F = {40^0}$.
B.
$\hat B = {40^0}$.
C.
$\hat D = {40^0}$.
D.
$\hat E = {40^0}$.

Câu 9 :

Cho tam giác ABC có: $\widehat A = {45^0};\widehat B = {60^0}$. So sánh các cạnh của tam giác ABC là:

A.
AB > AC > BC.
B.
AC > AB > BC.
C.
AB > BC > AC.
D.
AC > BC > AB.

Câu 10 :

Cho hình vẽ, hãy chỉ ra hai tam giác bằng nhau.

A.
$\Delta ABC = \Delta HEG$.
B.
$\Delta ABC = \Delta MNP$.
C.
$\Delta ABC = \Delta ISR$.
D.
$\Delta S{\rm{IR}} = \Delta MNP$.

Câu 11 :

Cho tam giác ABC cân tại A, cạnh AB = 5cm. Tính độ dài cạnh AC?

A.
10cm.
B.
2,5cm.
C.
7,5cm.
D.
5cm.

Câu 12 :

Cho hình vẽ, có bao nhiêu đường xiên kẻ từ điểm A đến đường thẳng BF?

A.
1.
B.
2.
C.
3.
D.
4.

II. Tự luận

Câu 1 :

1. Tìm x biết: $\frac{x}{4} = \frac{7}{5}$.

2. Cho biết đại lượng x và y tỉ lệ thuận với nhau và khi x = 20 thì y = 12.

a) Tìm hệ số tỉ lệ của y đối với x và biểu diễn y theo x.

b) Tính giá trị của x khi $y = \frac{{ - 1}}{3}$.

Câu 2 :

Ba lớp 7A, 7B, 7C thu tập tặng bạn vùng bão. Biết số vở của ba lớp lần lượt tỉ lệ với 3; 4; 5 và tổng số vở của lớp 7A và 7C là 240 cuốn. Tính số vở của mỗi lớp thu được.

Câu 3 :

Một đội công nhân có 15 người làm xong công việc trong 90 ngày. Hỏi cần bổ sung thêm bao nhiêu công nhân để hoàn thành công việc đó chỉ trong 50 ngày.

Câu 4 :

So sánh các cạnh của tam giác ABC có $\widehat A = {50^0},\,\widehat B = {60^0}$.

Câu 5 :

Cho tam giác ABC có AB = AC, N là trung điểm của BC.

a) Chứng minh $\Delta ABN = \Delta ACN$.

b) Qua A kẻ đường thẳng a vuông góc với AN. Chứng minh a // BC.

c) Vẽ điểm F sao cho N là trung điểm của AF. Chứng minh AB + AC > 2AN.

Lời giải và đáp án

I. Trắc nghiệm

Câu 1 :

Nếu 4.b = 5.c và b, c ≠ 0 thì:

A.
$\frac{4}{c} = \frac{b}{5}$.
B.
$\frac{b}{5} = \frac{c}{4}$.
C.
$\frac{4}{b} = \frac{5}{c}$.
D.
$\frac{c}{5} = \frac{b}{4}$.

Đáp án : B

Phương pháp giải :

Dựa vào tính chất của tỉ lệ thức: Nếu $ad = bc\left( {a,b,c,d \ne 0} \right)$ thì ta có các tỉ lệ thức:

$\frac{a}{b} = \frac{c}{d};\frac{a}{c} = \frac{b}{d};\frac{d}{b} = \frac{c}{a};\frac{d}{c} = \frac{b}{a}$

Lời giải chi tiết :

Nếu $4.b = 5.c$ thì ta có các tỉ lệ thức:

$\frac{4}{c} = \frac{5}{b};\frac{4}{5} = \frac{c}{b};\frac{c}{4} = \frac{b}{5};\frac{5}{4} = \frac{b}{c}$ nên B đúng.

Câu 2 :

Nếu các số x, y, z tỉ lệ với các số 6; 4; 3 thì ta có dãy tỉ số bằng nhau nào:

A.
$\frac{x}{4} = \frac{y}{3} = \frac{z}{6}$.
B.
$\frac{3}{x} = \frac{4}{y} = \frac{6}{z}$.
C.
$\frac{x}{3} = \frac{y}{4} = \frac{z}{6}$.
D.
$\frac{x}{6} = \frac{y}{4} = \frac{z}{3}$.

Đáp án : D

Phương pháp giải :

Dựa vào tính chất dãy tỉ số bằng nhau.

Lời giải chi tiết :

Nếu các số x, y, z tỉ lệ với các số 6; 4; 3 thì ta có dãy tỉ số bằng nhau:

$\frac{x}{6} = \frac{y}{4} = \frac{z}{3}$.

Câu 3 :

Đại lượng y tỉ lệ thuận với đại lượng x theo hệ số tỉ lệ 5. Ta có:

A.
y = 5.x.
B.
$y = \frac{1}{5}.x$.
C.
y = x.
D.
y = x + 5.

Đáp án : A

Phương pháp giải :

Dựa vào kiến thức về hai đại lượng tỉ lệ thuận.

Lời giải chi tiết :

Đại lượng y tỉ lệ thuận với đại lượng x theo hệ số tỉ lệ 5 ta có công thức $y = 5x$.

Câu 4 :

Cho x và y là hai đại lượng tỉ lệ thuận với nhau. Biết hệ số tỉ lệ của x đối với y là 8. Hệ số tỉ lệ của y đối với x là:

A.
5.
B.
8.
C.
$\frac{1}{8}$.
D.
5.

Đáp án : B

Phương pháp giải :

Khi đại lượng y tỉ lệ thuận với đại lượng x theo hệ số tỉ lệ k (khác 0) thì x cũng tỉ lệ thuận với y theo hệ số tỉ lệ $\frac{1}{k}$ và ta nói hai đại lượng đó tỉ lệ thuận với nhau.

Lời giải chi tiết :

Hệ số tỉ lệ của x đối với y là 8 nên hệ số tỉ lệ của y đối với x là $\frac{1}{8}$.

Câu 5 :

Cho biết y và x là hai đại lượng tỉ lệ nghịch theo hệ số tỉ lệ a. Ta có:

A.
y = ax.
B.
$y = \frac{a}{x}$.
C.
$x = \frac{y}{a}$.
D.
$y = a - x$.

Đáp án : B

Phương pháp giải :

Dựa vào kiến thức về hai đại lượng tỉ lệ nghịch.

Lời giải chi tiết :

Nếu y và x là hai đại lượng tỉ lệ nghịch theo hệ số tỉ lệ a thì $y = \frac{a}{x}$ hay $xy = a$.

Câu 6 :

Cho tam giác ABC. Trong các khẳng định sau khẳng định nào sai?

A.
$AB + AC > BC$.
B.
$AB + BC > AC$.
C.
$AC - BC > AB$.
D.
$AB < AC + BC$.

Đáp án : C

Phương pháp giải :

Dựa vào quan hệ giữa ba cạnh của một tam giác.

Lời giải chi tiết :

Trong một tam giác, tổng độ dài hai cạnh bất kỳ bao giờ cũng lớn hơn độ dài cạnh còn lại nên A, B và D đúng.

Trong một tam giác, hiệu độ dài hai cạnh bất kỳ bao giờ cũng nhỏ hơn độ dài cạnh còn lại nên C sai.

Câu 7 :

Cho $\Delta ABC = \Delta DEF$. Khi đó:

A.
AB = DE.
B.
AC = DE.
C.
BC = DF.
D.
BC = DE.

Đáp án : A

Phương pháp giải :

Dựa vào các kiến thức về hai tam giác bằng nhau.

Lời giải chi tiết :

$\Delta ABC = \Delta DEF$ nên ta có:

$\begin{array}{l}AB = DE\\BC = EF\\AC = DF\end{array}$

Câu 8 :

Cho $\Delta ABC = \Delta DEF$, $\hat C = {40^0}$. Khi đó:

A.
$\hat F = {40^0}$.
B.
$\hat B = {40^0}$.
C.
$\hat D = {40^0}$.
D.
$\hat E = {40^0}$.

Đáp án : A

Phương pháp giải :

Dựa vào các kiến thức về hai tam giác bằng nhau.

Lời giải chi tiết :

$\Delta ABC = \Delta DEF$ nên ta có:

$\widehat C = \widehat F = {40^0}$.

Câu 9 :

Cho tam giác ABC có: $\widehat A = {45^0};\widehat B = {60^0}$. So sánh các cạnh của tam giác ABC là:

A.
AB > AC > BC.
B.
AC > AB > BC.
C.
AB > BC > AC.
D.
AC > BC > AB.

Đáp án : A

Phương pháp giải :

Áp dụng định lí tổng ba góc của một tam giác và quan hệ giữa góc và cạnh đối diện trong một tam giác.

Lời giải chi tiết :

Xét tam giác ABC có:

$\begin{array}{l}\widehat A + \widehat B + \widehat C = {180^0}\\\widehat C = {180^0} - \widehat A - \widehat B\\ = {180^0} - {45^0} - {60^0}\\ = {75^0}\end{array}$

Trong tam giác ABC, ta có:

$\widehat C > \widehat B > \widehat A\left( {{{75}^0} > {{60}^0} > {{45}^0}} \right)$ suy ra $AB > AC > BC$.

Câu 10 :

Cho hình vẽ, hãy chỉ ra hai tam giác bằng nhau.

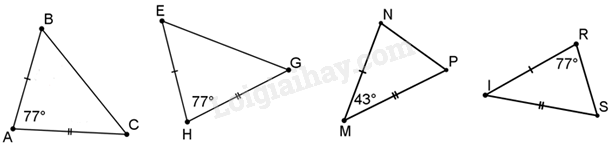
A.
$\Delta ABC = \Delta HEG$.
B.
$\Delta ABC = \Delta MNP$.
C.
$\Delta ABC = \Delta ISR$.
D.
$\Delta S{\rm{IR}} = \Delta MNP$.

Đáp án : A

Phương pháp giải :

Dựa vào các trường hợp bằng nhau của hai tam giác để xác định.

Lời giải chi tiết :

Trong các tam giác trên, chỉ có $\Delta ABC = \Delta HEG$(c.g.c) đủ điều kiện để xác định bằng nhau.

Câu 11 :

Cho tam giác ABC cân tại A, cạnh AB = 5cm. Tính độ dài cạnh AC?

A.
10cm.
B.
2,5cm.
C.
7,5cm.
D.
5cm.

Đáp án : D

Phương pháp giải :

Dựa vào tính chất của tam giác cân.

Lời giải chi tiết :

Tam giác ABC cân tại A nên AB = AC = 5cm.

Câu 12 :

Cho hình vẽ, có bao nhiêu đường xiên kẻ từ điểm A đến đường thẳng BF?

A.
1.
B.
2.
C.
3.
D.
4.

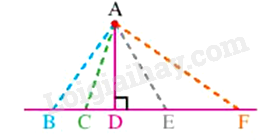
Đáp án : D

Phương pháp giải :

Dựa vào kiến thức về đường xiên.

Lời giải chi tiết :

Trong hình trên, có 4 đường xiên là: AB, AC, AE, AF.

II. Tự luận

Câu 1 :

1. Tìm x biết: $\frac{x}{4} = \frac{7}{5}$.

2. Cho biết đại lượng x và y tỉ lệ thuận với nhau và khi x = 20 thì y = 12.

a) Tìm hệ số tỉ lệ của y đối với x và biểu diễn y theo x.

b) Tính giá trị của x khi $y = \frac{{ - 1}}{3}$.

Phương pháp giải :

1. Dựa vào tính chất của tỉ lệ thức để tìm x.

2. Sử dụng kiến thức về hai đại lượng tỉ lệ thuận với nhau.

Lời giải chi tiết :

1. Ta có:

$\begin{array}{l}\frac{x}{4} = \frac{7}{5}\\5x = 7.4\\5x = 28\\x = \frac{{28}}{5}\end{array}$

Vậy $x = \frac{{28}}{5}$.

a) Vì đại lượng x và y tỉ lệ thuận với nhau nên $y = kx$ ($k \ne 0$)

Vì khi x = 20 thì y = 12 nên $20 = k.12$ suy ra $k = \frac{{20}}{{12}} = \frac{5}{3}$.

Vậy hệ số tỉ lệ của y đối với x là $k = \frac{5}{3}$ và $y = \frac{5}{3}x$.

b) Thay $y = \frac{{ - 1}}{3}$ vào công thức ta được: $\frac{{ - 1}}{3} = \frac{5}{3}x$ suy ra $x = \frac{{ - 1}}{5}$.

Câu 2 :

Phương pháp giải :

Áp dụng tính chất của dãy tỉ số bằng nhau để tìm số vở của mỗi lớp thu được.

Lời giải chi tiết :

Gọi số vở lớp 7A, 7B, 7C lần lượt là a, b, c $\left( {a,b,c \in \mathbb{N}*} \right)$ (cuốn)

Vì số học sinh lớp 7A, 7B, 7C tương ứng tỉ lệ với 3; 4; 5 nên ta có dãy tỉ số bằng nhau:

$\frac{a}{3} = \frac{b}{4} = \frac{c}{5}$

Do tổng số vở của lớp 7A và 7C là 240 nên áp dụng tính chất của dãy tỉ số bằng nhau, ta có:

$\frac{b}{4} = \frac{a}{3} = \frac{c}{5} = \frac{{a + c}}{{3 + 5}} = \frac{{240}}{8} = 30$.

Từ đó suy ra:

$\begin{array}{l}a = 30.3 = 90\\b = 30.4 = 120\\c = 30.5 = 150\end{array}$ (Thỏa mãn)

Vậy số vở lớp 7A, 7B, 7C thu được lần lượt là 90; 120; 150 cuốn.

Câu 3 :

Một đội công nhân có 15 người làm xong công việc trong 90 ngày. Hỏi cần bổ sung thêm bao nhiêu công nhân để hoàn thành công việc đó chỉ trong 50 ngày.

Phương pháp giải :

Áp dụng tính chất của hai đại lượng tỉ lệ nghịch với nhau.

Lời giải chi tiết :

Gọi số công nhân mà đội cần để hoàn thành công việc trong 50 ngày là x (người) ($x \in N*,x > 15$)

Vì lượng công việc là không thay đổi nên số công nhân và thời gian hoàn thành công việc là hai đại lượng tỉ lệ nghịch.

Theo tính chất của hai đại lượng tỉ lệ nghịch, ta có:

$15.90 = x.50$ suy ra $x = \frac{{15.90}}{{50}} = 27$.

Vậy đội cần bổ sung thêm 27 – 15 = 12 công nhân để hoàn thành công việc trong 50 ngày.

Câu 4 :

So sánh các cạnh của tam giác ABC có $\widehat A = {50^0},\,\widehat B = {60^0}$.

Phương pháp giải :

Áp dụng định lí tổng ba góc của một tam giác và quan hệ giữa góc và cạnh đối diện trong một tam giác.

Lời giải chi tiết :

Xét tam giác ABC có:

$\begin{array}{l}\widehat A + \widehat B + \widehat C = {180^0}\\\widehat C = {180^0} - \widehat A - \widehat B\\ = {180^0} - {50^0} - {60^0}\\ = {70^0}\end{array}$

Trong tam giác ABC, ta có:

$\widehat C > \widehat B > \widehat A\left( {{{70}^0} > {{60}^0} > {{50}^0}} \right)$ suy ra $AB > AC > BC$.

Câu 5 :

Cho tam giác ABC có AB = AC, N là trung điểm của BC.

a) Chứng minh $\Delta ABN = \Delta ACN$.

b) Qua A kẻ đường thẳng a vuông góc với AN. Chứng minh a // BC.

c) Vẽ điểm F sao cho N là trung điểm của AF. Chứng minh AB + AC > 2AN.

Phương pháp giải :

a) Dựa vào các trường hợp bằng nhau của hai tam giác.

b) Chứng minh $AN \bot BC$ suy ra a // BC.

c) Dựa vào bất đẳng thức tam giác để chứng minh.

Lời giải chi tiết :

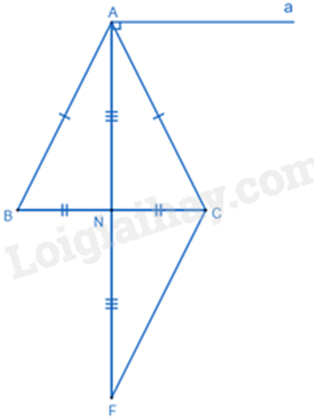
a) Xét $\Delta ABN$ và $\Delta ACN$ có:

$\begin{array}{l}AB = AC(gt)\\BN = CN(gt)\\AN\,chung\end{array}$

Suy ra $\Delta ABN = \Delta ACN$(c.c.c) (đpcm)

b) Ta có $\Delta ABN = \Delta ACN$ suy ra $\widehat {ANB} = \widehat {ANC}$.

Mà hai góc này là hai góc kề bù nên $\widehat {ANB} = \widehat {ANC} = \frac{{{{180}^0}}}{2} = {90^0}$.

Do đó $AN \bot BC$. Mà $a \bot AN$ (gt)

Suy ra $a//BC$ (từ vuông góc đến song song) (đpcm).

c) Xét $\Delta ABN$ và $\Delta FCN$ có:

$\begin{array}{l}AN = NF(gt)\\BN = CN(gt)\end{array}$

$\widehat {ANB} = \widehat {FNC}$ (hai góc đối đỉnh)

Suy ra $\Delta ABN = \Delta FCN$(c.g.c) (đpcm)

Suy ra AB = CF.

Xét $\Delta ACF$ có:

$\begin{array}{l}CF + AC > AF\\AB + AC > 2AN\end{array}$

(vì AB = CF và AF = 2AN) (đpcm).

Đề thi giữa kì 2 Toán 7 Chân trời sáng tạo - Đề số 8

Phần trắc nghiệm (3 điểm) Câu 1: Nếu 2.b = 5.c và b, c ≠ 0 thì:

Xem chi tiết

Đề thi giữa kì 2 Toán 7 Chân trời sáng tạo - Đề số 9

Phần trắc nghiệm (3 điểm) Câu 1: Thay tỉ số 1,2 : 1,35 bằng tỉ số giữa các số nguyên ta được:

Xem chi tiết

Đề thi giữa kì 2 Toán 7 Chân trời sáng tạo - Đề số 10

Phần trắc nghiệm (3 điểm) Câu 1: Từ tỉ lệ thức $\frac{a}{b}=\frac{c}{d}$ (giả thiết các tỉ số đều có nghĩa) ta suy ra đẳng thức:

Xem chi tiết

Đề thi giữa kì 2 Toán 7 Chân trời sáng tạo - Đề số 6

Phần trắc nghiệm (3 điểm) Câu 1: Trong các cặp tỉ số sau, cặp tỉ số nào lập thành một tỉ lệ thức?

Xem chi tiết

Đề thi giữa kì 2 Toán 7 - Đề số 5 - Chân trời sáng tạo

I. TRẮC NGHIỆM ( 2 điểm) Hãy chọn phương án trả lời đúng và viết chữ cái đứng trước đáp án đó vào bài làm.

Xem chi tiết

Đề thi giữa kì 2 Toán 7 - Đề số 4 - Chân trời sáng tạo

I. TRẮC NGHIỆM ( 2 điểm) Hãy chọn phương án trả lời đúng và viết chữ cái đứng trước đáp án đó vào bài làm.

Xem chi tiết

Đề thi giữa kì 2 Toán 7 - Đề số 3 - Chân trời sáng tạo

I. TRẮC NGHIỆM ( 2 điểm) Hãy chọn phương án trả lời đúng và viết chữ cái đứng trước đáp án đó vào bài làm.

Xem chi tiết

Đề thi giữa kì 2 Toán 7 - Đề số 2 - Chân trời sáng tạo

I. TRẮC NGHIỆM ( 3 điểm) Hãy chọn phương án trả lời đúng và viết chữ cái đứng trước đáp án đó vào bài làm.

Xem chi tiết

Đề thi giữa kì 2 Toán 7 - Đề số 1 - Chân trời sáng tạo

I. TRẮC NGHIỆM (2,0 điểm) Hãy chọn phương án trả lời đúng và viết chữ cái đứng trước đáp án đó vào bài làm.

Xem chi tiết

>> Học trực tuyến lớp 7 trên Tuyensinh247.com Đầy đủ khoá học các bộ sách (Kết nối tri thức với cuộc sống; Chân trời sáng tạo; Cánh diều). Cam kết giúp học sinh lớp 7 học tốt, hoàn trả học phí nếu học không hiệu quả.