Đề thi giữa kì 1 Toán 11 Chân trời sáng tạo - Đề số 10
Đề thi giữa kì 1 Toán 11 Chân trời sáng tạo - Đề số 10
Đề bài
Cho góc lượng giác $\left( {Oa,Ob} \right)$ có số đo là $50^\circ .$ Hỏi số đo của góc luọng giác nào trong bốn đáp án A, B, C, D bên dưới cũng có tia đầu là $Oa$ và tia cuối là $Ob?$
-
A.
\({\alpha _1} = 140^\circ .\)
-
B.
\({\alpha _2} = 410^\circ .\)
-
C.
\({\alpha _3} = 320^\circ .\)
-
D.
\({\alpha _4} = 230^\circ .\)
Cho một góc lượng giác (Ox, Ou) có số đo \( - {30^o}\) và một góc lượng giác (Ox, Ov) có số đo \({120^o}\). Tính số đo góc lượng giác (Ou, Ov).
-
A.
\({150^o} + k{360^o}(k \in Z)\)
-
B.
\( - {150^o} + k{360^o}\) \((k \in Z)\)
-
C.
\({90^o} + k{360^o}\) \((k \in Z)\)
-
D.
\( - {90^o} + k{360^o}\) \((k \in Z)\)
Góc có số đo \(\frac{{7\pi }}{4}\) radian bằng bao nhiêu độ?
-
A.
\({315^o}\)
-
B.
\({45^o}\)
-
C.
\({345^o}\)
-
D.
\({275^o}\)
Bánh xe đạp có bán kính 50cm. Một người quay bánh xe 5 vòng quanh trục thì quãng đường đi được là:
-
A.
\(250\pi (cm)\)
-
B.
\(1000\pi (cm)\)
-
C.
\(500\pi (cm)\)
-
D.
\(200\pi (cm)\)
Cho góc $\alpha $ thỏa mãn $\cos \alpha = \frac{3}{5}$. Giá trị của $P = \cos 2\alpha $ là
-
A.
$P = - \frac{2}{5}.$
-
B.
$P = - \frac{7}{{25}}.$
-
C.
$P = \frac{{16}}{{25}}.$
-
D.
$P = \frac{4}{5}.$
Cho dãy số \(\left( {{u_n}} \right)\) với \({u_n} = \frac{{{{( - 1)}^{n - 1}}}}{{n + 1}}\). Số hạng thứ 9 của dãy là
-
A.
\({u_9} = \frac{1}{{10}}\)
-
B.
\({u_9} = \frac{{ - 1}}{{10}}\)
-
C.
\({u_9} = \frac{{ - 1}}{9}\)
-
D.
\({u_9} = \frac{1}{9}\)
Trong các dãy số sau dãy số nào là dãy số tăng?
-
A.
$4;\,9;\,14;\,19;\,24$.
-
B.
$9;\,7;\,5;\,3;\,1;\,0$.
-
C.
$\frac{1}{2};\,\frac{2}{5};\,\frac{3}{7};\,\frac{4}{9};\,\frac{5}{{12}}$.
-
D.
\(0;\,1;\,2;\, - 3;\,7\).
Dãy số nào sau đây là dãy số bị chặn?
-
A.
\({a_n} = \sqrt {n + 10} \).
-
B.
${b_n} = \sqrt {5n + 10} $.
-
C.
${u_n} = \sqrt {n + 10} + \sqrt {20 - n} $.
-
D.
${v_n} = \sqrt {5n - 6} $.
Trong các dãy số sau, dãy số nào không phải là cấp số cộng?
-
A.
\(\frac{1}{2};\,\,\frac{3}{2};\,\,\frac{5}{2};\,\,\frac{7}{2};\,\,\frac{9}{2}.\)
-
B.
\(1;\,\,1;\,\,1;\,\,1;\,\,1.\)
-
C.
\( - 8;\,\, - 6;\,\, - 4;\,\, - 2;\,\,0.\)
-
D.
\(3;\,\,1;\,\, - 1;\,\, - 2;\,\, - 4.\)
Trong các dãy số sau, dãy số nào không phải là một cấp số nhân?
-
A.
$1;\,\,\,1\,\,;\,\,1;\,\,1;...$
-
B.
$2;\,\,4;\,\,8;\,\,16;...$
-
C.
$\sqrt 2 ;\,\,2;\,\,2\sqrt 2 ;\,\,4\sqrt 2 ;...$
-
D.
$1;\,\, - \frac{1}{3};\,\,\frac{1}{9};\,\, - \frac{1}{{27}};...$
Trong các khẳng định sau, khẳng định nào đúng?
-
A.
Qua 2 điểm phân biệt có duy nhất một mặt phẳng.
-
B.
Qua 3 điểm phân biệt bất kì có duy nhất một mặt phẳng.
-
C.
Qua 3 điểm không thẳng hàng có duy nhất một mặt phẳng.
-
D.
Qua 4 điểm phân biệt bất kì có duy nhất một mặt phẳng.
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành tâm O. Gọi E là trung điểm của SA. Mặt phẳng nào dưới đây chứa đường thẳng OE?
-
A.
(SBC)
-
B.
(ABCD)
-
C.
(SAC)
-
D.
(CDE)
Cho phương trình lượng giác \(\cos 2x = - \frac{1}{2}\) (*).
a) Phương trình (*) tương đương với phương trình: \(\cos 2x = \cos \left( { - \frac{\pi }{3}} \right)\).
b) Nghiệm dương nhỏ nhất của phương trình (*) bằng \(\frac{\pi }{3}\).
c) Tổng các nghiệm của phương trình (*) trong khoảng \(\left( {0;\pi } \right)\) bằng \(\frac{{3\pi }}{2}\).
d) Trong khoảng \(\left( {0;\pi } \right)\) phương trình (*) có 3 nghiệm.
Anh Bình là nhân viên của một công ty A. Từ ngày 1/2/2024 anh Bình được nâng lương lên bậc 4, mức lương anh hiện hưởng là 11.718.750 đồng mỗi tháng (chưa trừ thuế và bảo hiểm). Theo quy định của công ty, nếu không bị kỷ luật, không có khen thưởng đặc biệt thì cứ sau 3 năm anh Bình sẽ được nâng một bậc lương, tăng thêm 25% so với bậc lương trước, tối đa là bậc 7. Khi hết bậc 7 sẽ chuyển sang vượt khung. Lương vượt khung năm sau cao hơn năm trước 1% và vẫn nhận hàng tháng. Lương bậc 1 sẽ được tính sau khi hết đúng 1 năm tập sự. Anh Bình là người rất nghiêm túc, không vi phạm kỷ luật. Anh dự định sẽ làm việc 30 năm ở công ty này rồi nghỉ hưu.
Các mệnh đề sau đúng hay sai? (làm tròn đến đồng).
a) Lương bậc 5 của anh Bình sẽ là 14.500.000 đồng.
b) Lương bậc 1 của anh Bình là 6.000.000 đồng.
c) Lương bậc 7 anh Bình là 23.250.000 đồng.
d) Tổng tiền lương anh Bình nhận được kể từ khi hết tập sự đến khi nghỉ hưu là 5.554.357.709 đồng.
Số giờ có ánh sáng của thành phố T ở vĩ độ $40^{o}$ bắc trong ngày thứ t của một năm không nhuận được cho bởi hàm số $d(t) = 3 \cdot \sin\left\lbrack {\dfrac{\pi}{182}(t - 80)} \right\rbrack + 12$ với $t \in {\mathbb{Z}}$ và $0 < t \leq 365$. Bạn An muốn đi tham quan thành phố T nhưng lại không thích ánh sáng mặt trời, vậy bạn An nên chọn đi vào ngày nào trong năm để thành phố T có ít giờ có ánh sáng mặt trời nhất?
Litva là một nước trong liên minh Châu Âu, đã gia nhập khu vực đồng tiền chung Châu Âu thông qua việc sử dụng đồng Euro vào ngày 01 tháng 01 năm 2015. Để kỷ niệm thời khắc lịch sử này, chính quyền đất nước Litva quyết định dùng 122550 đồng tiền xu Litas Lithuania cũ của đất nước để xếp một mô hình kim tự tháp. Biết rằng tầng dưới cùng có 4901 đồng và cứ lên thêm một tầng thì số đồng xu giảm đi 100 đồng. Hỏi mô hình Kim tự tháp này có tất cả bao nhiêu tầng?

Một loại thuốc được dùng mỗi ngày một lần. Lúc đầu nồng độ thuốc trong máu của bệnh nhân tăng nhanh, nhưng mỗi liều kế tiếp có tác dụng ít hơn liều trước đó. Lượng thuốc trong máu ở ngày thứ nhất là 50mg, và mỗi ngày sau đó giảm chỉ còn một nửa so với ngày kể trước đó. Tính tổng lượng thuốc (tính bằng mg) trong máu của bệnh nhân sau khi dùng thuốc 10 ngày liên tiếp. (Kết quả được làm tròn đến hàng phần mười).
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi M, N lần lượt là trung điểm của các cạnh SB và CD. Đường thẳng SN cắt mặt phẳng (MAD) tại K. Biết SK = xKN. Tính x.
Lời giải và đáp án
Cho góc lượng giác $\left( {Oa,Ob} \right)$ có số đo là $50^\circ .$ Hỏi số đo của góc luọng giác nào trong bốn đáp án A, B, C, D bên dưới cũng có tia đầu là $Oa$ và tia cuối là $Ob?$
-
A.
\({\alpha _1} = 140^\circ .\)
-
B.
\({\alpha _2} = 410^\circ .\)
-
C.
\({\alpha _3} = 320^\circ .\)
-
D.
\({\alpha _4} = 230^\circ .\)
Đáp án : B
Các góc lượng giác có cùng tia đầu và tia cuối hơn kém nhau \(k{360^o}\).
Xét đáp án A: \({140^o} - {50^o} = {90^o}\).
Xét đáp án B: \({410^o} - {50^o} = {360^o}\).
Xét đáp án C: \({320^o} - {50^o} = {270^o}\).
Xét đáp án D: \({230^o} - {50^o} = {180^o}\).
Các góc lượng giác có cùng tia đầu và tia cuối hơn kém nhau \(k{360^o}\) nên chỉ có đáp án B thỏa mãn.
Cho một góc lượng giác (Ox, Ou) có số đo \( - {30^o}\) và một góc lượng giác (Ox, Ov) có số đo \({120^o}\). Tính số đo góc lượng giác (Ou, Ov).
-
A.
\({150^o} + k{360^o}(k \in Z)\)
-
B.
\( - {150^o} + k{360^o}\) \((k \in Z)\)
-
C.
\({90^o} + k{360^o}\) \((k \in Z)\)
-
D.
\( - {90^o} + k{360^o}\) \((k \in Z)\)
Đáp án : A
Sử dụng hệ thức Chasles: Với ba tia Ou, Ov, Ow bất kì, ta có:
sđ (Ou,Ov) + sđ (Ov,Ow) = sđ (Ou,Ow) + \(k{360^0}(k \in Z)\)
Với ba tia Ox, Ou, Ov bất kì, ta có:
sđ (Ox, Ou) + sđ (Ou, Ov) = sđ (Ox, Ov) \( + k{360^o}\) \((k \in \mathbb{Z})\)
\( - {30^o}\) + sđ (Ou, Ov) = \({120^o} + k{360^o}\)
sđ (Ou, Ov) = \({150^o} + k{360^o}\).
Góc có số đo \(\frac{{7\pi }}{4}\) radian bằng bao nhiêu độ?
-
A.
\({315^o}\)
-
B.
\({45^o}\)
-
C.
\({345^o}\)
-
D.
\({275^o}\)
Đáp án : A
Áp dụng quan hệ giữa radian và độ: \(1rad = {\left( {\frac{{180}}{\pi }} \right)^o}\), \({1^o} = \frac{\pi }{{180}}rad\).
Ta có: \(\frac{{7\pi }}{4}rad = \frac{{7\pi }}{4}.\frac{{{{180}^o}}}{\pi } = {315^o}\).
Bánh xe đạp có bán kính 50cm. Một người quay bánh xe 5 vòng quanh trục thì quãng đường đi được là:
-
A.
\(250\pi (cm)\)
-
B.
\(1000\pi (cm)\)
-
C.
\(500\pi (cm)\)
-
D.
\(200\pi (cm)\)
Đáp án : C
Một cung của đường tròn bán kính R và có số đo \(\alpha\) rad thì có độ dài \(l=R\alpha\).
Ta có R = 50 cm suy ra:
\(l = R\alpha = 50.2\pi .5 = 500\pi\) (cm).
Cho góc $\alpha $ thỏa mãn $\cos \alpha = \frac{3}{5}$. Giá trị của $P = \cos 2\alpha $ là
-
A.
$P = - \frac{2}{5}.$
-
B.
$P = - \frac{7}{{25}}.$
-
C.
$P = \frac{{16}}{{25}}.$
-
D.
$P = \frac{4}{5}.$
Đáp án : B
Sử dụng công thức nhân đôi \(\cos 2\alpha = 2{\cos ^2}\alpha - 1\).
Ta có \(P = \cos 2\alpha = 2{\cos ^2}\alpha - 1 = 2{\left( {\frac{3}{5}} \right)^2} - 1 = - \frac{7}{{25}}\).
Cho dãy số \(\left( {{u_n}} \right)\) với \({u_n} = \frac{{{{( - 1)}^{n - 1}}}}{{n + 1}}\). Số hạng thứ 9 của dãy là
-
A.
\({u_9} = \frac{1}{{10}}\)
-
B.
\({u_9} = \frac{{ - 1}}{{10}}\)
-
C.
\({u_9} = \frac{{ - 1}}{9}\)
-
D.
\({u_9} = \frac{1}{9}\)
Đáp án : A
Thay 9 vào n và tính.
\({u_9} = \frac{{{{( - 1)}^{9 - 1}}}}{{9 + 1}} = \frac{1}{{10}}\).
Trong các dãy số sau dãy số nào là dãy số tăng?
-
A.
$4;\,9;\,14;\,19;\,24$.
-
B.
$9;\,7;\,5;\,3;\,1;\,0$.
-
C.
$\frac{1}{2};\,\frac{2}{5};\,\frac{3}{7};\,\frac{4}{9};\,\frac{5}{{12}}$.
-
D.
\(0;\,1;\,2;\, - 3;\,7\).
Đáp án : A
Dãy số tăng có mọi số hạng lớn hơn số hạng liền trước nó.
Chỉ có dãy A là dãy số tăng.
Dãy số nào sau đây là dãy số bị chặn?
-
A.
\({a_n} = \sqrt {n + 10} \).
-
B.
${b_n} = \sqrt {5n + 10} $.
-
C.
${u_n} = \sqrt {n + 10} + \sqrt {20 - n} $.
-
D.
${v_n} = \sqrt {5n - 6} $.
Đáp án : C
Dãy số bị chặn là dãy số vừa bị chặn trên, vừa bị chặn dưới.
Xét ${u_n} = \sqrt {n + 10} + \sqrt {20 - n} $.
Ta có:
\(\left\{ {\begin{array}{*{20}{c}}{n + 10 \ge 0}\\{20 - n \ge 0}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{n \ge - 10}\\{n \le 20}\end{array}} \right. \Rightarrow n \le 20\) (vì \(n \in \mathbb{N}^*\)).
Dãy số chỉ có 20 số hạng nên dãy bị chặn.
Trong các dãy số sau, dãy số nào không phải là cấp số cộng?
-
A.
\(\frac{1}{2};\,\,\frac{3}{2};\,\,\frac{5}{2};\,\,\frac{7}{2};\,\,\frac{9}{2}.\)
-
B.
\(1;\,\,1;\,\,1;\,\,1;\,\,1.\)
-
C.
\( - 8;\,\, - 6;\,\, - 4;\,\, - 2;\,\,0.\)
-
D.
\(3;\,\,1;\,\, - 1;\,\, - 2;\,\, - 4.\)
Đáp án : D
Dựa vào định nghĩa cấp số cộng.
Dãy A là cấp số cộng với công sai d = 1.
Dãy B là cấp số cộng với công sai d = 0.
Dãy C là cấp số cộng với công sai d = 2.
Dãy D không phải cấp số cộng.
Trong các dãy số sau, dãy số nào không phải là một cấp số nhân?
-
A.
$1;\,\,\,1\,\,;\,\,1;\,\,1;...$
-
B.
$2;\,\,4;\,\,8;\,\,16;...$
-
C.
$\sqrt 2 ;\,\,2;\,\,2\sqrt 2 ;\,\,4\sqrt 2 ;...$
-
D.
$1;\,\, - \frac{1}{3};\,\,\frac{1}{9};\,\, - \frac{1}{{27}};...$
Đáp án : C
Dựa vào định nghĩa cấp số nhân.
Dãy đáp án A là cấp số nhân với số hạng đầu là 1, công bội bằng 1.
Dãy đáp án B là cấp số nhân với số hạng đầu là 2, công bội bằng 2.
Dãy đáp án D là cấp số nhân với số hạng đầu là 1, công bội bằng \( - \frac{1}{3}\).
Dãy đáp án C không phải cấp số nhân.
Trong các khẳng định sau, khẳng định nào đúng?
-
A.
Qua 2 điểm phân biệt có duy nhất một mặt phẳng.
-
B.
Qua 3 điểm phân biệt bất kì có duy nhất một mặt phẳng.
-
C.
Qua 3 điểm không thẳng hàng có duy nhất một mặt phẳng.
-
D.
Qua 4 điểm phân biệt bất kì có duy nhất một mặt phẳng.
Đáp án : C
Dựa vào lý thuyết các tính chất được thừa nhận về đường thẳng và mặt phẳng.
Có một và chỉ một mặt phẳng đi qua 3 điểm không thẳng hàng.
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành tâm O. Gọi E là trung điểm của SA. Mặt phẳng nào dưới đây chứa đường thẳng OE?
-
A.
(SBC)
-
B.
(ABCD)
-
C.
(SAC)
-
D.
(CDE)
Đáp án : C
Mặt phẳng cần tìm chứa cả hai điểm O và E.
Ta có \(\left\{ \begin{array}{l}O \in AC\\E \in SA\end{array} \right.\) nên \(OE \subset (SAC)\).
Cho phương trình lượng giác \(\cos 2x = - \frac{1}{2}\) (*).
a) Phương trình (*) tương đương với phương trình: \(\cos 2x = \cos \left( { - \frac{\pi }{3}} \right)\).
b) Nghiệm dương nhỏ nhất của phương trình (*) bằng \(\frac{\pi }{3}\).
c) Tổng các nghiệm của phương trình (*) trong khoảng \(\left( {0;\pi } \right)\) bằng \(\frac{{3\pi }}{2}\).
d) Trong khoảng \(\left( {0;\pi } \right)\) phương trình (*) có 3 nghiệm.
a) Phương trình (*) tương đương với phương trình: \(\cos 2x = \cos \left( { - \frac{\pi }{3}} \right)\).
b) Nghiệm dương nhỏ nhất của phương trình (*) bằng \(\frac{\pi }{3}\).
c) Tổng các nghiệm của phương trình (*) trong khoảng \(\left( {0;\pi } \right)\) bằng \(\frac{{3\pi }}{2}\).
d) Trong khoảng \(\left( {0;\pi } \right)\) phương trình (*) có 3 nghiệm.
Áp dụng công thức nghiệm của phương trình lượng giác cơ bản: \(\cos x = \cos \alpha \Leftrightarrow x = \pm \alpha + k2\pi \), \(k \in \mathbb{Z}\).
a) Sai. \(\cos 2x=-\frac{1}{2}\Leftrightarrow \cos 2x=\cos \left( \frac{2\pi }{3} \right)\).
b) Đúng. \( \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{2x = \frac{{2\pi }}{3} + k2\pi }\\{2x = - \frac{{2\pi }}{3} + k2\pi }\end{array}(k \in \mathbb{Z}) \Rightarrow \left[ {\begin{array}{*{20}{l}}{x = \frac{\pi }{3} + k\pi }\\{x = - \frac{\pi }{3} + k\pi }\end{array}(k \in \mathbb{Z})} \right.} \right.\).
\(0 < x < \pi \Rightarrow \left[ {\begin{array}{*{20}{l}}{0 < \frac{\pi }{3} + k\pi < \pi }\\{0 < - \frac{\pi }{3} + k\pi < \pi }\end{array}(k \in \mathbb{Z}) \Rightarrow \left[ {\begin{array}{*{20}{l}}{k = 0}\\{k = 1}\end{array}} \right. \Rightarrow \left[ {\begin{array}{*{20}{l}}{x = \frac{\pi }{3}}\\{x = \frac{{2\pi }}{3}}\end{array}} \right.} \right.\).
Do \(\frac{{2\pi }}{3} > \frac{\pi }{3}\) nghiệm dương nhỏ nhất của phương trình là \(x = \frac{\pi }{3}\).
c) Sai. Tổng các nghiệm của phương trình trong khoảng \(\left( {0;\pi } \right)\) là: $S=\frac{\pi }{3}+\frac{2\pi }{3}=\pi $.
d) Sai. Trong khoảng \(\left( {0;\pi } \right)\) phương trình (*) có 2 nghiệm là \(x = \frac{\pi }{3}\) và \(x = \frac{{2\pi }}{3}\).
Anh Bình là nhân viên của một công ty A. Từ ngày 1/2/2024 anh Bình được nâng lương lên bậc 4, mức lương anh hiện hưởng là 11.718.750 đồng mỗi tháng (chưa trừ thuế và bảo hiểm). Theo quy định của công ty, nếu không bị kỷ luật, không có khen thưởng đặc biệt thì cứ sau 3 năm anh Bình sẽ được nâng một bậc lương, tăng thêm 25% so với bậc lương trước, tối đa là bậc 7. Khi hết bậc 7 sẽ chuyển sang vượt khung. Lương vượt khung năm sau cao hơn năm trước 1% và vẫn nhận hàng tháng. Lương bậc 1 sẽ được tính sau khi hết đúng 1 năm tập sự. Anh Bình là người rất nghiêm túc, không vi phạm kỷ luật. Anh dự định sẽ làm việc 30 năm ở công ty này rồi nghỉ hưu.
Các mệnh đề sau đúng hay sai? (làm tròn đến đồng).
a) Lương bậc 5 của anh Bình sẽ là 14.500.000 đồng.
b) Lương bậc 1 của anh Bình là 6.000.000 đồng.
c) Lương bậc 7 anh Bình là 23.250.000 đồng.
d) Tổng tiền lương anh Bình nhận được kể từ khi hết tập sự đến khi nghỉ hưu là 5.554.357.709 đồng.
a) Lương bậc 5 của anh Bình sẽ là 14.500.000 đồng.
b) Lương bậc 1 của anh Bình là 6.000.000 đồng.
c) Lương bậc 7 anh Bình là 23.250.000 đồng.
d) Tổng tiền lương anh Bình nhận được kể từ khi hết tập sự đến khi nghỉ hưu là 5.554.357.709 đồng.
Áp dụng công thức số hạng tổng quát và tổng n số hạng đầu của cấp số nhân.
Gọi \({u_n}\) là mức lương bậc n của anh Bình.
Dãy \(\left( {{u_n}} \right)\) là một cấp số nhân với số hạng đầu \({u_1}\), công bội q = 1,25.
a) Sai. Lương bậc 5 của anh Bình là:
\({u_5} = {u_4}.q = 11718750.1,25 \approx 14648438\) (đồng).
b) Đúng. Ta có \({u_4} = {u_1}.{q^3} \Leftrightarrow 11718750 = {u_1}.1,{25^3} \Leftrightarrow {u_1} = 6000000\).
Vậy mức lương bậc 1 của anh Bình là 6.000.000 đồng.
c) Sai. Lương bậc 7 của anh Bình là:
\({u_7} = {u_1}.{q^6} = 6000000.1,{25^6} \approx 228888184\) (đồng).
d) Sai.
Từ năm 1 đến năm 3: lương bậc 1.
Từ năm 4 đến năm 6: lương bậc 2.
…
Từ năm 19 đến năm 21: lương bậc 7.
Từ năm 22 đến năm 30: lương vượt khung.
Tổng số lương anh Bình nhận được từ năm 1 đến năm 21 là:
\({S_1} = 12.3.\frac{{6000000.(1 - 1,{{25}^7})}}{{1 - 1,25}} \approx 3255873047\) (đồng).
(Mỗi bậc lương sẽ được nhận trong 12.3 = 36 tháng).
Tổng số lương anh Bình nhận được từ năm 22 đến năm 30 là:
\({S_2} \approx 12.\frac{{22888184.(1 - 1,{{01}^9})}}{{1 - 1,{{01}^9}}} \approx 2573142865\) (đồng).
(Mỗi bậc lương vượt khung sẽ nhận được trong 1 năm = 12 tháng).
Vậy tổng tiền lương anh Bình nhận được đến khi nghỉ hưu là:
\({S_1} + {S_2} \approx 5829015912\) (đồng).
Số giờ có ánh sáng của thành phố T ở vĩ độ $40^{o}$ bắc trong ngày thứ t của một năm không nhuận được cho bởi hàm số $d(t) = 3 \cdot \sin\left\lbrack {\dfrac{\pi}{182}(t - 80)} \right\rbrack + 12$ với $t \in {\mathbb{Z}}$ và $0 < t \leq 365$. Bạn An muốn đi tham quan thành phố T nhưng lại không thích ánh sáng mặt trời, vậy bạn An nên chọn đi vào ngày nào trong năm để thành phố T có ít giờ có ánh sáng mặt trời nhất?
Áp dụng kiến thức về tập giá trị của hàm sin.
Ta có: \(\sin \left[ {\frac{\pi }{{182}}\left( {t - 80} \right)} \right] \ge - 1\)nên \(d\left( t \right)\) nhỏ nhất khi \(\sin \left[ {\frac{\pi }{{182}}\left( {t - 80} \right)} \right] = - 1\).
\(\sin \left[ {\frac{\pi }{{182}}\left( {t - 80} \right)} \right] = - 1\)
\( \Leftrightarrow \frac{\pi }{{182}}\left( {t - 80} \right) = \frac{{3\pi }}{2} + k2\pi \)
\( \Leftrightarrow t - 80 = 273 + 364k\)
\( \Leftrightarrow t = 353 + 364k\).
Vì \(t \in \mathbb{Z}\) và \(0 < t \le 365\) nên lấy \(k = 0\) ta có \(t = 353\).
Litva là một nước trong liên minh Châu Âu, đã gia nhập khu vực đồng tiền chung Châu Âu thông qua việc sử dụng đồng Euro vào ngày 01 tháng 01 năm 2015. Để kỷ niệm thời khắc lịch sử này, chính quyền đất nước Litva quyết định dùng 122550 đồng tiền xu Litas Lithuania cũ của đất nước để xếp một mô hình kim tự tháp. Biết rằng tầng dưới cùng có 4901 đồng và cứ lên thêm một tầng thì số đồng xu giảm đi 100 đồng. Hỏi mô hình Kim tự tháp này có tất cả bao nhiêu tầng?

- Bài toán về cấp số cộng.
- Tổng của n số hạng đầu tiên trong CSC có số hạng đầu tiên là $u_1$ và công sai là d là:
$S_n = \frac{[2u_1 + (n-1)d]n}{2}$.
Bài toán là bài tập về cấp số cộng nếu ta coi số đồng xu ở tầng dưới cùng là số hạng đầu với công sai là hiệu số đồng xu của tầng 2 tầng liền kề.
Khi đó, ta có một cấp số cộng với $u_1 = 4901$ và công sai d = -100.
Gọi số tầng của kim tự tháp đó là $n$ ($n \in \mathbb{N}^*$).
Khi đó, tổng số đồng xu của $n$ tầng đó là $S_n = 122550$ nên ta có:
$S_n = \frac{[2u_1 + (n-1)d]n}{2}$
$\Leftrightarrow 122550 = \frac{[2 \cdot 4901 + (n-1) \cdot (-100)] \cdot n}{2}$
$\Leftrightarrow 245100 = [2 \cdot 4901 - 100n + 100] \cdot n$
$\Leftrightarrow 245100 = [9902 - 100n] . n$
$\Leftrightarrow 100n^2 - 9902n + 245100 = 0$
$\Leftrightarrow n = 50 \ (tm)$ hoặc $n = \frac{2451}{50} \ (ktm)$
Vậy mô hình kim tự tháp đã cho có 50 tầng.
Một loại thuốc được dùng mỗi ngày một lần. Lúc đầu nồng độ thuốc trong máu của bệnh nhân tăng nhanh, nhưng mỗi liều kế tiếp có tác dụng ít hơn liều trước đó. Lượng thuốc trong máu ở ngày thứ nhất là 50mg, và mỗi ngày sau đó giảm chỉ còn một nửa so với ngày kể trước đó. Tính tổng lượng thuốc (tính bằng mg) trong máu của bệnh nhân sau khi dùng thuốc 10 ngày liên tiếp. (Kết quả được làm tròn đến hàng phần mười).
Áp dụng công thức tính tổng n số hạng đầu của cấp số nhân.
Lượng thuốc ở ngày thứ nhất là 50 mg.
Lượng thuốc ở ngày thứ hai là \(50.\frac{1}{2} = 25\) mg.
Lượng thuốc ở ngày thứ ba là \(50.{\left( {\frac{1}{2}} \right)^2} = \frac{{25}}{2}\) mg.
…
Lượng thuốc ở ngày thứ n là \(50.{\left( {\frac{1}{2}} \right)^{n - 1}}\) mg.
Lượn thuốc mỗi ngày lập thành cấp số nhân với số hạng đầu \({u_1} = 50\), công bội \(q = \frac{1}{2}\).
Tổng lượng thuốc khi dùng 10 ngày liên tiếp là:
\({S_{10}} = {u_1}.\frac{{1 - {q^{10}}}}{{1 - q}} = 50.\frac{{1 - {{\left( {\frac{1}{2}} \right)}^{10}}}}{{1 - \frac{1}{2}}} = \frac{{25575}}{{256}} \approx 99,9\) (mg).
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi M, N lần lượt là trung điểm của các cạnh SB và CD. Đường thẳng SN cắt mặt phẳng (MAD) tại K. Biết SK = xKN. Tính x.
Áp dụng tính chất của hai đường thẳng song song, tính chất trọng tâm, đường trung bình của tam giác.
Để tìm giao điểm của đường thẳng và mặt phẳng, ta tìm một điểm thuộc cả đường thẳng và mặt phẳng đó.

Vì AD // BC nên giao tuyến của hai mặt phẳng (MAD) và (SBC) là đường thẳng MP // AD // BC (P thuộc SC).
Vì MP // BC nên theo định lí Thales ta có \(\frac{{SM}}{{MB}} = \frac{{SP}}{{PC}} = 1\) và P cũng là trung điểm của SC.
Xét trong (SCD), ta có SN cắt DP tại K’, do đó \(\left\{ \begin{array}{l}K' \in SN\\K' \in DP \subset (MAD)\end{array} \right.\)
Suy ra K’ là giao của SN và (MAD), hay K’ trùng K.
Có DP và SN là hai đường trung tuyến của tam giác SCD và chúng giao nhau tại K. Do đó K là trọng tâm của tam giác SCD. Suy ra SK = 2KN. Vậy x = 2.
a) Thay \(n = 1,{\rm{ }}2,{\rm{ 3, 4}}\) vào công thức \({u_n} = \sin \left[ {\left( {2n - 1} \right)\frac{\pi }{4}} \right]\) để xác định 4 số hạng đầu của dãy số.
b) Thay \(n\) bởi \(n + 4\) vào công thức \({u_n} = \sin \left[ {\left( {2n - 1} \right)\frac{\pi }{4}} \right]\) để xác định \({u_{n + 4}}\) và chú ý rằng \(\sin \left( {x + k2\pi } \right) = \sin x\).
c) Sử dụng kết quả câu b, ta có \({u_1} = {u_5} = {u_9}\), \({u_2} = {u_6} = {u_{10}}\), \({u_3} = {u_7} = {u_{11}}\), \({u_4} = {u_8} = {u_{12}}\). Do đó tổng 12 số hạng đầu tiên bằng \(3\left( {{u_1} + {u_2} + {u_3} + {u_4}} \right)\).
a) Ta có:
\({u_1} = \sin \left[ {\left( {2.1 - 1} \right)\frac{\pi }{4}} \right] = \sin \frac{\pi }{4} = \frac{{\sqrt 2 }}{2}\);
\({u_2} = \sin \left[ {\left( {2.2 - 1} \right)\frac{\pi }{4}} \right] = \sin \frac{{3\pi }}{4} = \frac{{\sqrt 2 }}{2}\);
\({u_3} = \sin \left[ {\left( {2.3 - 1} \right)\frac{\pi }{4}} \right] = \sin \frac{{5\pi }}{4} = - \frac{{\sqrt 2 }}{2}\);
\({u_4} = \sin \left[ {\left( {2.4 - 1} \right)\frac{\pi }{4}} \right] = \sin \frac{{7\pi }}{4} = - \frac{{\sqrt 2 }}{2}\).
Như vậy 4 số hạng đầu của dãy số là: \(\frac{{\sqrt 2 }}{2},\frac{{\sqrt 2 }}{2}, - \frac{{\sqrt 2 }}{2}, - \frac{{\sqrt 2 }}{2}\).
b) Ta có:
\({u_{n + 4}} = \sin \left\{ {\left[ {2\left( {n + 4} \right) - 1} \right]\frac{\pi }{4}} \right\} = \sin \left[ {\left( {2n - 1 + 8} \right)\frac{\pi }{4}} \right] \)
\(= \sin \left[ {\left( {2n - 1} \right)\frac{\pi }{4} + 2\pi } \right] = \sin \left[ {\left( {2n - 1} \right)\frac{\pi }{4}} \right] = {u_n}\).
Vậy \({u_{n + 4}} = {u_n}\) với \(\forall n \in {\mathbb{N}^*}\).
c) Theo câu b, ta có \({u_{n + 4}} = {u_n}\) với \(\forall n \in {\mathbb{N}^*}\). Như vậy \({u_1} = {u_5} = {u_9}\), \({u_2} = {u_6} = {u_{10}}\), \({u_3} = {u_7} = {u_{11}}\), \({u_4} = {u_8} = {u_{12}}\).
Do đó:
\({u_1} + {u_2} + {u_3} + ... + {u_{12}} = 3\left( {{u_1} + {u_2} + {u_3} + {u_4}} \right) \)
\(= 3\left( {\frac{{\sqrt 2 }}{2} + \frac{{\sqrt 2 }}{2} + \frac{{ - \sqrt 2 }}{2} + \frac{{ - \sqrt 2 }}{2}} \right) = 0\).
Xét dấu \(\cos x\) khi \(x \in \left( {\pi ;\frac{{3\pi }}{2}} \right)\).
Thay vào đẳng thức \({\sin ^2}x + {\cos ^2}x = 1\) ta tìm được \(\cos x\).
Áp dụng công thức cộng:
\(\cos \left( {a - b} \right) = \cos a.\cos b + \sin a.\sin b\).
\(x \in \left( {\pi ;\frac{{3\pi }}{2}} \right) \Rightarrow \cos x < 0\).
\(\Rightarrow \cos x = - \sqrt {1 - {{\sin }^2}x} \)
\(= - \sqrt {1 - {{\left( { - \frac{1}{3}} \right)}^2}} = - \frac{{2\sqrt 2 }}{3}\).
Ta tính được: \(\cos x = - \frac{{2\sqrt 2 }}{3}\).
Khi đó: \(\cos \left( {2x - \frac{\pi }{3}} \right) = \frac{1}{2}\cos 2x + \frac{{\sqrt 3 }}{2}\sin 2x\)
\( = \frac{1}{2}(1 - 2{\sin ^2}x) + \sqrt 3 \sin x\cos x = \frac{{7 + 4\sqrt 6 }}{{18}}\).
a) Tìm 2 điểm chung của 2 mặt phẳng (SAC) và (SBD). Giao tuyến của 2 mặt phẳng là đường thẳng đi qua 2 điểm chung đó.
b) Chứng minh NG song song với 1 đường thẳng thuộc (SAC).
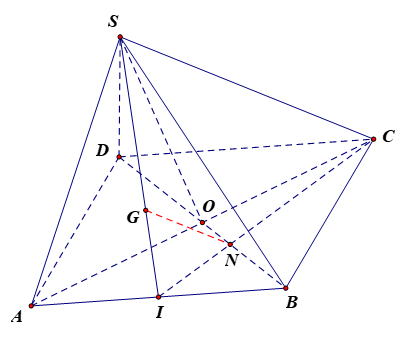
a) Ta có:
\(\left\{ \begin{array}{l}S \in (SAC)\\O \in AC \subset (SAC)\end{array} \right.\) suy ra \(SO \subset (SAC)\).
\(\left\{ \begin{array}{l}S \in (SBD)\\O \in BD \subset (SBD)\end{array} \right.\) suy ra \(SO \subset (SBD)\).
Vậy SO là giao tuyến của (SAC) và (SBD).
b) Gọi I là trung điểm của AB.
Xét tam giác ABC có N là trọng tâm và CI là trung tuyến, ta có: \(\frac{{IN}}{{IC}} = \frac{1}{3}\).
Xét tam giác SAB có G là trọng tâm và SI là trung tuyến, ta có: \(\frac{{IG}}{{IS}} = \frac{1}{3}\).
Xét tam giác SIC có \(G \in SI\), \(N \in IC\) và \(\frac{{IG}}{{IS}} = \frac{{IN}}{{IC}} = \frac{1}{3}\).
Suy ra GN//SC (định lý Thales đảo).
Mà SC thuộc mặt phẳng (SAC) và GN không thuộc mặt phẳng (SAC).
Vậy GN//(SAC).
Đề thi giữa kì 1 Toán 11 Chân trời sáng tạo - Đề số 9
Phần trắc nghiệm
Phần trắc nghiệm
Phần trắc nghiệm
Câu 1: Góc lượng giác nào dưới đây tương ứng với chuyển động quay (2frac{1}{5}) vòng theo chiều kim đồng hồ?
Câu 1: Góc lượng giác nào dưới đây tương ứng với chuyển động quay \(3\frac{2}{5}\) vòng ngược chiều kim đồng hồ?
Câu 1: Giá trị biểu thức \(P = {\cos ^2}\frac{\pi }{3} - \tan \frac{\pi }{4} + {\cot ^2}\frac{\pi }{6} + \sin \frac{\pi }{2}\) là:
Câu 1: Cho góc lượng giác (Ov, Ow) có số đo là \(\frac{{4\pi }}{5}\), góc lượng giác (Ou, Ow) có số đo là \(\frac{{7\pi }}{5}\). Số đo góc lượng giác (Ou, Ov) là:
Câu 1: Cho góc lượng giác (Ou, Ov) có số đo là (frac{{2pi }}{5}), góc lượng giác (Ou, Ow) có số đo là (frac{{3pi }}{5}). Số đo góc lượng giác (Ov, Ow) là:
>> 2K9 Học trực tuyến - Định hướng luyện thi TN THPT, ĐGNL, ĐGTD ngay từ lớp 11 (Xem ngay) cùng thầy cô giáo giỏi trên Tuyensinh247.com. Bứt phá điểm 9,10 chỉ sau 3 tháng, tiếp cận sớm các kì thi.
 |
 |
 |
 |
 |
 |
 |
 |










Danh sách bình luận