Đề tham khảo thi vào 10 môn Toán Hà Nội năm 2025 - Đề số 11

Đề bài

Câu 1: (1,5 điểm)

1) Cân nặng của các bạn học sinh lớp 9A (đơn vị: kilogam) có kết quả như sau:

Mẫu số liệu thống kê ở trên đã được ghép thành năm nhóm ứng với năm nửa khoảng: [50;55), [55;60), [60;65), [65;70), [70;75). Lập bảng tần số ghép nhóm của mẫu số liệu trên và tính tần số tương đối ghép nhóm của nhóm [50;55).

2) Một hộp đựng 20 tấm thẻ như nhau được đánh số từ 1 đến 20. Rút ngẫu nhiên một tấm thẻ trong hộp. Tính xác suất của biến cố A: “Số ghi trên tấm thẻ là bội của 4”.

Câu 2: (1,5 điểm) Cho hai biểu thức \(P = \frac{{3\sqrt x }}{{\sqrt x  + 2}} + \frac{{\sqrt x }}{{2 - \sqrt x }} + \frac{{8\sqrt x }}{{x - 4}}\) và \(Q = \frac{1}{{\sqrt x  + 2}}\) (với \(x \ge 0\), \(x \ne 4\)).

1) Tính giá trị của biểu thức Q khi x = 9.

2) Rút gọn biểu thức P.

3) Biết \(M = \frac{P}{Q}\). Tìm các giá trị của x để M = 18.

Câu 3: (2,5 điểm)

1) Mai mua hai loại hàng và phải trả tổng cộng 165 000 đồng, trong đó đã tính 15 000 đồng là thuế giá trị gia tăng (viết tắt là VAT). Biết rằng thuế VAT với loại hàng thứ nhất là 12%, thuế VAT với loại hàng thứ hai là 9%. Hỏi nếu không kể thuế thì Mai phải trả bao nhiêu tiền cho mỗi loại hàng?

2) Hưởng ứng phong trào thi đua “Xây dựng trường học thân thiện, học sinh tích cực”, lớp 9A trường THCS Hoàng Hoa Thám dự định trồng 300 cây xanh. Đến ngày lao động, có 5 bạn được Liên Đội triệu tập tham gia chiến dịch an toàn giao thông nên mỗi bạn còn lại phải trồng thêm 2 cây mới đảm bảo kế hoạch đặt ra. Hỏi lớp 9A có bao nhiêu học sinh?

3) Phương trình \({x^2} - 2x - m + 1 = 0\) (m là tham số) có một nghiệm là \(x = 1 + \sqrt 7 \). Tính giá trị của biểu thức \(A = {x_1}^2{x_2} + {x_2}^2{x_1}\).

Câu 4: (4 điểm)

1) Trong truyện ngụ ngôn La Phông ten, Cò mời Cáo đến ăn tiệc với món súp hảo hạng. Món súp đó Cò thường cho vào một cái bình hình trụ, có bán kính đáy là 4 cm, chiều cao 30 cm. Nhưng khi Cáo đến, Cò chỉ đổ súp sao cho phần súp trong bình đó cao 10 cm và mới Cáo dùng bữa.

a) Tính thể tích của phần súp mà Cò mời Cáo ăn.

b) Cổ của Cáo quá ngắn nên không thể lấy được súp, Cáo nhìn quanh và phát hiện ra nhà Cò có những viên sỏi hình cầu giống hệt nhau, bán kính 2 cm. Cáo bèn cho từng viên sỏi vào bình súp đến khi súp dâng lên vừa đầy đến miệng bình rồi Cáo thảnh thơi ăn súp. Hỏi Cáo đã cho vào bình bao nhiêu viên sỏi?

2) Cho đường tròn (O;R) và dây MN cố định (MN < 2R). Kẻ đường kính AB vuông góc với dây MN tại E (điểm A thuộc cung nhỏ MN). Lấy điểm C thuộc dây MN (C khác M, N, E). Đường thẳng BC cắt (O;R) tại điểm K (K khác B).

a) Chứng minh AKCE là tứ giác nội tiếp.

b) Chứng minh \(B{M^2} = BK.BC\).

c) Gọi I là giao điểm của hai đường thẳng AK và MN; D là giao điểm của hai đường thẳng AC và BI. Chứng minh C cách đều ba cạnh của \(\Delta DEK\).

Câu 5: (0,5 điểm) Công ty sản xuất thùng gỗ muốn thiết kế số lượng lớn thùng đựng hàng hóa bên trong, dang hình lăng trụ tứ giác đều không nắp với thể tích là 62,5 \(d{m^3}\). Để tiết kiệm vật gỗ làm thùng, người ta cần thiết kế thùng sao cho có tổng S diện tích xung quanh và diện tích mặt đáy là nhỏ nhất. Hỏi S có giá trị nhỏ nhất bằng bao nhiêu?

Lời giải chi tiết

Câu 1: (1,5 điểm)

1) Cân nặng của các bạn học sinh lớp 9A (đơn vị: kilogam) có kết quả như sau:

Mẫu số liệu thống kê ở trên đã được ghép thành năm nhóm ứng với năm nửa khoảng: [50;55), [55;60), [60;65), [65;70), [70;75). Lập bảng tần số ghép nhóm của mẫu số liệu trên và tính tần số tương đối ghép nhóm của nhóm [50;55).

2) Một hộp đựng 20 tấm thẻ như nhau được đánh số từ 1 đến 20. Rút ngẫu nhiên một tấm thẻ trong hộp. Tính xác suất của biến cố A: “Số ghi trên tấm thẻ là bội của 4”.

Phương pháp

1) Xác định tần số cho các nhóm để lập bảng tần số ghép nhóm.

Tần số tương đối của nhóm bằng: tần số của nhóm : tổng . 100%.

2) Xác định không gian mẫu của phép thử, tính số phần tử của không gian mẫu.

Tính số kết quả thuận lợi của biến cố.

Xác suất của biến cố = số kết quả thuận lợi của biến cố : số phần tử của không gian mẫu.

Lời giải

1) Bảng tần số ghép nhóm của mẫu số liệu trên:

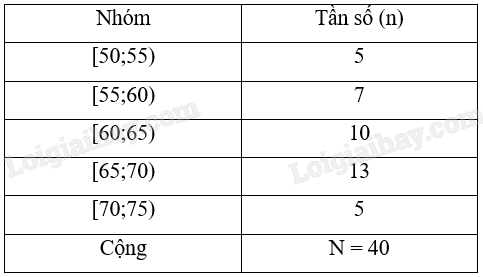
Tần số tương đối ghép nhóm của nhóm [50;55) là \(\frac{5}{{40}}.100\%  = 12,5\% \).

2) Số phần tử của không gian mẫu là \(n\left( \Omega  \right) = 20\).

Kết quả thuận lợi cho biến cố A là {4; 8; 12; 16; 20}, suy ra n(A) = 5.

Vậy xác suất của biến cố A là \(P(A) = \frac{{n\left( A \right)}}{{n\left( \Omega  \right)}} = \frac{5}{{20}} = \frac{1}{4}\).

Câu 2: (1,5 điểm) Cho hai biểu thức \(P = \frac{{3\sqrt x }}{{\sqrt x  + 2}} + \frac{{\sqrt x }}{{2 - \sqrt x }} + \frac{{8\sqrt x }}{{x - 4}}\) và \(Q = \frac{1}{{\sqrt x  + 2}}\) (với \(x \ge 0\), \(x \ne 4\)).

1) Tính giá trị của biểu thức Q khi x = 9.

2) Rút gọn biểu thức P.

3) Biết \(M = \frac{P}{Q}\). Tìm các giá trị của x để M = 18.

Phương pháp

1) Kiểm tra điều kiện của x. Nếu thỏa mãn, thay x = 9 vào Q.

2) Kết hợp các tính chất của căn thức bậc hai để rút gọn biểu thức.

3) Rút gọn \(M = \frac{P}{Q}\) rồi giải phương trình M = 18.

Lời giải

1) Thay x = 9 (thỏa mãn điều kiện) vào Q, ta được:

\(Q = \frac{1}{{\sqrt 9  + 2}} = \frac{1}{{3 + 2}} = \frac{1}{5}\).

Vậy khi x = 9 thì \(Q = \frac{1}{5}\).

2) \(P = \frac{{3\sqrt x }}{{\sqrt x  + 2}} + \frac{{\sqrt x }}{{2 - \sqrt x }} + \frac{{8\sqrt x }}{{x - 4}}\) (với \(x \ge 0\), \(x \ne 4\))

\( = \frac{{3\sqrt x }}{{\sqrt x  + 2}} - \frac{{\sqrt x }}{{\sqrt x  - 2}} + \frac{{8\sqrt x }}{{\left( {\sqrt x  + 2} \right)\left( {\sqrt x  - 2} \right)}}\)

\( = \frac{{3\sqrt x \left( {\sqrt x  - 2} \right)}}{{\left( {\sqrt x  + 2} \right)\left( {\sqrt x  - 2} \right)}} - \frac{{\sqrt x \left( {\sqrt x  + 2} \right)}}{{\left( {\sqrt x  + 2} \right)\left( {\sqrt x  - 2} \right)}} + \frac{{8\sqrt x }}{{\left( {\sqrt x  + 2} \right)\left( {\sqrt x  - 2} \right)}}\)

\( = \frac{{3x - 6\sqrt x  - x - 2\sqrt x  + 8\sqrt x }}{{\left( {\sqrt x  + 2} \right)\left( {\sqrt x  - 2} \right)}}\)

\( = \frac{{2x}}{{\left( {\sqrt x  + 2} \right)\left( {\sqrt x  - 2} \right)}}\).

3) \(M = \frac{P}{Q} = \frac{{2x}}{{\left( {\sqrt x  + 2} \right)\left( {\sqrt x  - 2} \right)}}:\frac{1}{{\sqrt x  + 2}} = \frac{{2x}}{{\left( {\sqrt x  + 2} \right)\left( {\sqrt x  - 2} \right)}}.\left( {\sqrt x  + 2} \right) = \frac{{2x}}{{\sqrt x  - 2}}\).

Để M = 18 thì \(\frac{{2x}}{{\sqrt x  - 2}} = 18\)

\(2x = 18\left( {\sqrt x  - 2} \right)\)

\(2x - 18\sqrt x  + 36 = 0\)

\(x - 9\sqrt x  + 18 = 0\).

Giải phương trình trên, ta được \(\sqrt x  = 3\) hoặc \(\sqrt x  = 6\).

Suy ra x = 9 hoặc x = 36 (cả hai nghiệm đều thỏa mãn).

Vậy để M = 18 thì \(x \in \{ 9;36\} \).

Câu 3: (2,5 điểm)

1) Mai mua hai loại hàng và phải trả tổng cộng 165 000 đồng, trong đó đã tính 15 000 đồng là thuế giá trị gia tăng (viết tắt là VAT). Biết rằng thuế VAT với loại hàng thứ nhất là 12%, thuế VAT với loại hàng thứ hai là 9%. Hỏi nếu không kể thuế thì Mai phải trả bao nhiêu tiền cho mỗi loại hàng?

2) Hưởng ứng phong trào thi đua “Xây dựng trường học thân thiện, học sinh tích cực”, lớp 9A trường THCS Hoàng Hoa Thám dự định trồng 300 cây xanh. Đến ngày lao động, có 5 bạn được Liên Đội triệu tập tham gia chiến dịch an toàn giao thông nên mỗi bạn còn lại phải trồng thêm 2 cây mới đảm bảo kế hoạch đặt ra. Hỏi lớp 9A có bao nhiêu học sinh?

3) Phương trình \({x^2} - 2x - m + 1 = 0\) (m là tham số) có một nghiệm là \(x = 1 + \sqrt 7 \). Tính giá trị của biểu thức \(A = {x_1}^2{x_2} + {x_2}^2{x_1}\).

Phương pháp

1) Gọi x, y lần lượt là số tiền của loại hàng thứ nhất và loại hàng thứ hai không kể thuế VAT mà Mai đã mua (đồng; x , y > 0).

Biểu diễn tổng số tiền Mai phải trả và tổng số tiền thuế theo x, y.

Lập hệ phương trình, giải hệ tìm x, y.

2) Gọi số học sinh lớp 9A là x (học sinh; \(x \in {\mathbb{N}^*}\), x > 5).

Biểu diễn số cây mỗi học sinh phải trồng theo kế hoạch và thực tế.

Vì thực tế mỗi học sinh phải trồng thêm 2 cây so với kế hoạch nên ta lập được phương trình.

Giải phương trình và kết luận.

3) Thay nghiệm vào phương trình, tính m.

Biến đổi biểu thức và áp dụng định lí Viète: \(S = {x_1} + {x_2} =  - \frac{b}{a}\); \(P = {x_1}.{x_2} = \frac{c}{a}\).

Lời giải

1) Gọi x, y lần lượt là số tiền của loại hàng thứ nhất và loại hàng thứ hai không kể thuế VAT mà Mai đã mua (đồng; x , y > 0).

Số tiền thuế của hai loại hàng lần lượt là 12%x = 0,12x (đồng) và 9%y = 0,09y (đồng).

Vì tổng số tiền thuế là 15 000 đồng nên ta có phương trình \(0,12x + 0,09y = 15000\) (1)

Số tiền mua loại hàng thứ nhất sau tính thuế là x + 0,12x = 1,12x (đồng), số tiền mua loại hàng thứ hai sau tính thuế là y + 0,09y = 1,09y (đồng).

Vì số tiền phải trả tổng cộng là 165 000 cả thuế nên ta có phương trình \(1,12x + 1,09y = 165000\) (2)

Từ (1) và (2) ta có hệ phương trình \(\left\{ \begin{array}{l}0,12x + 0,09 = 15000\\1,12x + 1,09y = 165000\end{array} \right.\)

Giải hệ trên, ta được x = 50 000 (thỏa mãn) và y = 100 000 (thỏa mãn).

Vậy giá tiền không kể thuế của loại hàng thứ nhất là 50 000 đồng, giá tiền không kể thuế của loại hàng thứ hai là 100 000 đồng.

2) Gọi số học sinh lớp 9A là x (học sinh; \(x \in {\mathbb{N}^*}\), x > 5).

Số học sinh thực tế tham gia trồng cây là x – 5 (học sinh).

Theo kế hoạch, mỗi học sinh phải trồng \(\frac{{300}}{x}\) (cây).

Thực tế, mỗi học sinh phải trồng \(\frac{{300}}{{x - 5}}\) (cây).

Vì thực tế, mỗi học sinh phải trồng thêm 2 cây so với kế hoạch nên ta có phương trình:

\(\frac{{300}}{{x - 5}} - \frac{{300}}{x} = 2\)

\(\frac{{300x}}{{x(x - 5)}} - \frac{{300(x - 5)}}{{x(x - 5)}} = \frac{{2x(x - 5)}}{{x(x - 5)}}\)

\(300x - 300(x - 5) = 2x(x - 5)\)

\(300x - 300x + 1500 = 2{x^2} - 10x\)

\(2{x^2} - 10x - 1500 = 0\)

\({x^2} - 5x - 750 = 0\).

Giải phương trình trên, được x = 30 (thỏa mãn) và x = -25 (loại).

Vậy lớp 9A có 30 học sinh.

3) Thay \(x = 1 + \sqrt 7 \) vào phương trình, ta có: \({\left( {1 + \sqrt 7 } \right)^2} - 2\left( {1 + \sqrt 7 } \right) - m + 1 = 0\)

\(8 + 2\sqrt 7  - 2 - 2\sqrt 7  - m + 1 = 0\)

\(m = 7\).

Vậy phương trình đã cho là \({x^2} - 2x - 6 = 0\).

Gọi \({x_1}\), \({x_2}\) là hai nghiệm của phương trình.

Áp dụng hệ thức Viète: \(\left\{ \begin{array}{l}{x_1} + {x_2} =  - \frac{b}{a} =  - \frac{{ - 2}}{1} = 2\\{x_1}{x_2} = \frac{c}{a} = \frac{{ - 6}}{1} =  - 6\end{array} \right.\)

Ta có \(A = {x_1}^2{x_2} + {x_2}^2{x_1} = {x_1}{x_2}\left( {{x_1} + {x_2}} \right) =  - 6.2 =  - 12\).

Vậy A = -12.

Câu 4: (4 điểm)

1) Trong truyện ngụ ngôn La Phông ten, Cò mời Cáo đến ăn tiệc với món súp hảo hạng. Món súp đó Cò thường cho vào một cái bình hình trụ, có bán kính đáy là 4 cm, chiều cao 30 cm. Nhưng khi Cáo đến, Cò chỉ đổ súp sao cho phần súp trong bình đó cao 10 cm và mới Cáo dùng bữa.

a) Tính thể tích của phần súp mà Cò mời Cáo ăn.

b) Cổ của Cáo quá ngắn nên không thể lấy được súp, Cáo nhìn quanh và phát hiện ra nhà Cò có những viên sỏi hình cầu giống hệt nhau, bán kính 2 cm. Cáo bèn cho từng viên sỏi vào bình súp đến khi súp dâng lên vừa đầy đến miệng bình rồi Cáo thảnh thơi ăn súp. Hỏi Cáo đã cho vào bình bao nhiêu viên sỏi?

2) Cho đường tròn (O;R) và dây MN cố định (MN < 2R). Kẻ đường kính AB vuông góc với dây MN tại E (điểm A thuộc cung nhỏ MN). Lấy điểm C thuộc dây MN (C khác M, N, E). Đường thẳng BC cắt (O;R) tại điểm K (K khác B).

a) Chứng minh AKCE là tứ giác nội tiếp.

b) Chứng minh \(B{M^2} = BK.BC\).

c) Gọi I là giao điểm của hai đường thẳng AK và MN; D là giao điểm của hai đường thẳng AC và BI. Chứng minh C cách đều ba cạnh của \(\Delta DEK\).

Phương pháp

1)

a) Áp dụng công thức tính thể tích hình trụ \(V = \pi {r^2}h\).

b) Thể tích các viên sỏi = Thể tích bình – Thể tích lượng nước ban đầu.

Tính thể tích mỗi viên sỏi áp dụng công thức \(V = \frac{4}{3}\pi {r^3}\).

Số viên sỏi = Thể tích các viên sỏi : Thể tích mỗi viên sỏi.

2)

a) Chứng minh \(\widehat {AKC} = \widehat {AEC} = {90^o}\) suy ra K, E cùng thuộc đường tròn đường kính AC.

b) Chứng minh $\Delta BMK\backsim \Delta BCM$ (g.g) rồi suy ra tỉ lệ thức.

c) Chứng minh C là giao điểm của hai đường phân giác trong \(\Delta DEK\).

Lời giải

1)

a) Thể tích phần súp Cò mới Cáo ăn là \({V_1} = \pi {.4^2}.10 = 160\pi \) \(\left( {c{m^3}} \right)\).

b) Thể tích bình trụ là \({V_0} = \pi {.4^2}.30 = 480\pi \) \(\left( {c{m^3}} \right)\).

Vì súp dâng đầy bình khi Cáo thả các viên sỏi vào nên thể tích các viên sỏi là:

\(V = {V_0} - {V_1} = 480\pi  - 160\pi  = 320\pi \) \(\left( {c{m^3}} \right)\).

Thể tích 1 viên sỏi là \({V_{soi}} = \frac{4}{3}\pi {.2^3} = \frac{{32}}{3}\pi \) \(\left( {c{m^3}} \right)\).

Số viên sỏi được thả vào bình là \(320\pi :\frac{{32}}{3}\pi  = 30\) (viên).

Vậy Cáo đã cho 30 viên sỏi vào bình.

2)

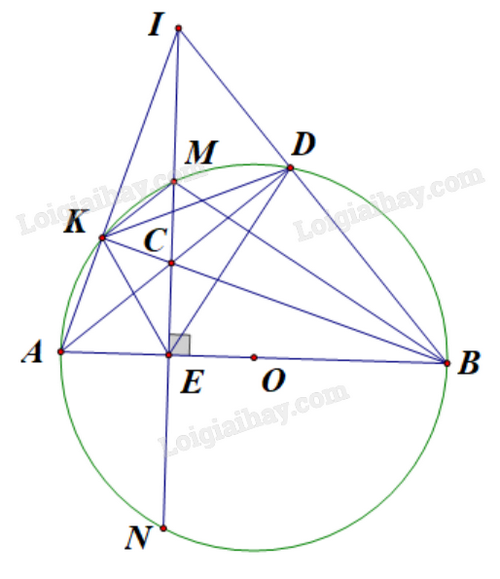
a) Vì K thuộc đường tròn đường kính AB nên \(\widehat {AKC} = {90^o}\).

Theo giả thiết, \(MN \bot AB\) nên \(\widehat {AEC} = {90^o}\).

Vì \(\widehat {AKC} = \widehat {AEC} = {90^o}\) nên K, E cùng thuộc đường tròn đường kính AC.

Vậy AKCE là tứ giác nội tiếp.

b) Vì AKCE là tứ giác nội tiếp nên \(\widehat {KAE} + \widehat {KCE} = {180^o}\).

Mặt khác, AKMB là tứ giác nội tiếp (O;R) nên \(\widehat {KAE} + \widehat {KMB} = {180^o}\).

Suy ra \(\widehat {KCE} = \widehat {KMB}\) (cùng bù với \(\widehat {KAE}\)); mà \(\widehat {KCE} = \widehat {MCB}\) (góc đối đỉnh) nên \(\widehat {KMB} = \widehat {MCB}\left( { = \widehat {KCE}} \right)\).

Xét \(\Delta BMK\) và \(\Delta BCM\) có:

+ \(\widehat {MBC}\) chung;

+ \(\widehat {KMB} = \widehat {MCB}\) (chứng minh trên).

Do đó $\Delta BMK\backsim \Delta BCM$ (g.g), suy ra \(\frac{{BM}}{{BC}} = \frac{{BK}}{{BM}}\), như vậy \(B{M^2} = BC.BK\).

c) Xét \(\Delta IAB\) có hai đường cao BK, IE cắt nhau tại C, do đó C là trực tâm \(\Delta IAB\).

Khi đó AD cũng là đường cao của \(\Delta IAB\), hay \(AD \bot IB\).

Vì \(\widehat {ADB} = {90^o}\) nên D thuộc đường tròn đường kính AB, hay D thuộc (O;R).

Vì tứ giác AKDB nội tiếp (O;R) nên \(\widehat {DKB} = \widehat {DAB}\) (góc nội tiếp cùng chắn cung BD).

Mà tứ giác AKCE nội tiếp (chứng minh trên) nên \(\widehat {BKE} = \widehat {DAB}\) (góc nội tiếp cùng chắn cung CE).

Suy ra \(\widehat {DKB} = \widehat {BKE}\left( { = \widehat {DAB}} \right)\) hay KB là phân giác của \(\widehat {DKE}\).

Vì \(\widehat {CDB} = \widehat {CEB} = {90^o}\) nên D, E thuộc đường tròn đường kính BC hay tứ giác BDCE nội tiếp.

Khi đó \(\widehat {EBC} = \widehat {EDC}\) (góc nội tiếp cùng chắn cung CE).

Mà tứ giác AKDB nội tiếp nên \(\widehat {EBC} = \widehat {CDK}\) (góc nội tiếp cùng chắn cung AK).

Suy ra \(\widehat {EDC} = \widehat {CDK}\left( { = \widehat {EBC}} \right)\) hay DC là phân giác của \(\widehat {KDE}\).

Xét \(\Delta DEK\) có các đường phân giác góc \(\widehat {DKE}\), \(\widehat {KDE}\) cắt nhau tại C.

Do đó, C là tâm đường tròn nội tiếp \(\Delta DEK\), hay C cách đều các cạnh của \(\Delta DEK\).

Câu 5: (0,5 điểm) Công ty sản xuất thùng gỗ muốn thiết kế số lượng lớn thùng đựng hàng hóa bên trong, dang hình lăng trụ tứ giác đều không nắp với thể tích là 62,5 \(d{m^3}\). Để tiết kiệm vật gỗ làm thùng, người ta cần thiết kế thùng sao cho có tổng S diện tích xung quanh và diện tích mặt đáy là nhỏ nhất. Hỏi S có giá trị nhỏ nhất bằng bao nhiêu?

Phương pháp

Gọi a là độ dài cạnh đáy của hình lăng trụ (dm; a > 0).

Biểu diễn diện tích S theo a.

Áp dụng bất đẳng thức Cauchy cho ba số dương, tìm giá trị nhỏ nhất của S.

Lời giải

Gọi a là độ dài cạnh đáy của hình lăng trụ (dm; a > 0).

Thùng gỗ là lăng trụ tứ giác đều nên đáy thùng là hình vuông có diện tích \({a^2}\) \(\left( {d{m^2}} \right)\).

Thể tích lăng trụ là 62,5 \(d{m^3}\) nên chiều cao là \(h = \frac{{62,5}}{{{a^2}}}\) (dm).

Diện tích gỗ làm một chiếc thùng là:

\(S = 4.\frac{{62,5}}{{{a^2}}}.a + {a^2} = \frac{{250}}{a} + {a^2} = \frac{{125}}{a} + \frac{{125}}{a} + {a^2}\) \(\left( {d{m^2}} \right)\).

Áp dụng bất đẳng thức Cauchy cho ba số dương \(\frac{{125}}{a}\), \(\frac{{125}}{a}\), \({a^2}\), ta có:

\(S = \frac{{125}}{a} + \frac{{125}}{a} + {a^2} \ge 3.\sqrt[3]{{\frac{{125}}{a}.\frac{{125}}{a}.{a^2}}} = 75\).

Dấu “=” xảy ra khi \(\frac{{125}}{a} = {a^2}\), suy ra a = 5.

Vậy S nhỏ nhất bằng 75 \(d{m^2}\) khi độ dài cạnh đáy là 5 dm.