Copyright © 2021 loigiaihay.com
Từ điển Toán 12 | Các dạng bài tập Toán 12
Vecto trong không gian - Từ điển môn Toán 12
Vecto trong không gian - Từ điển môn Toán 12 Cách phân tích một vecto theo các vecto cho trước - Toán 12
1. Cách phân tích một vecto theo các vecto cho trước
Để phân tích vecto \(\overrightarrow x \) theo các vecto \(\overrightarrow {{x_1}} \), \(\overrightarrow {{x_2}} \),…, \(\overrightarrow {{x_n}} \) cho trước, ta chèn các điểm để xuất hiện \(\overrightarrow {{x_1}} \), \(\overrightarrow {{x_2}} \),…, \(\overrightarrow {{x_n}} \) và biến đổi đến khi nào chỉ còn \(\overrightarrow {{x_1}} \), \(\overrightarrow {{x_2}} \),…, \(\overrightarrow {{x_n}} \) và các hệ số của chúng.
2. Ví dụ minh hoạ
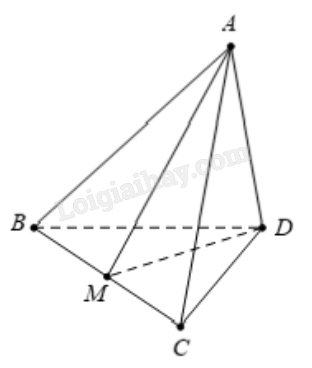
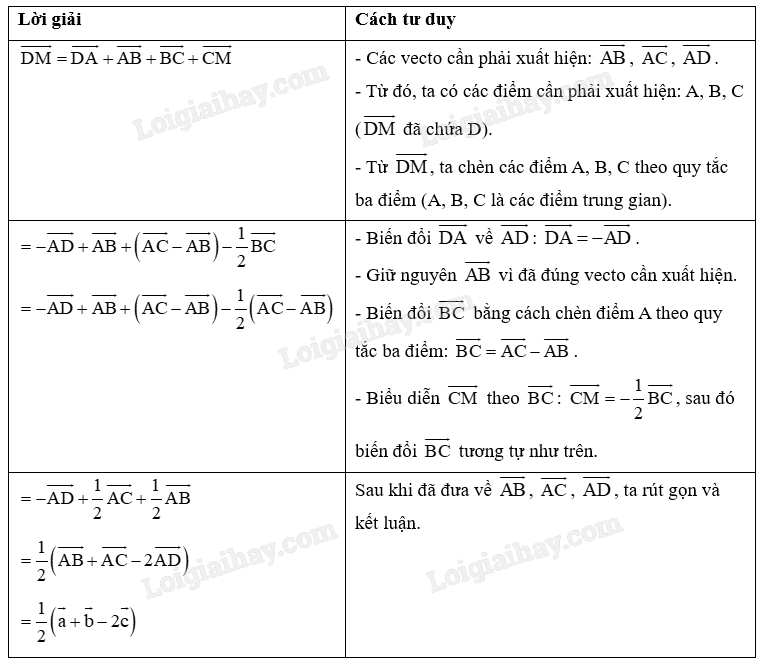
Cho tứ diện ABCD. Đặt \(\overrightarrow {AB} = \overrightarrow a \), \(\overrightarrow {AC} = \overrightarrow b \), \(\overrightarrow {AD} = \overrightarrow c \). Gọi M là trung điểm của đoạn thẳng BC. Phân tích \(\overrightarrow {DM} \) theo các vecto \(\overrightarrow a \), \(\overrightarrow b \), \(\overrightarrow c \).
Giải:
