Cách tính cường độ hợp lực trong không gian - Toán 12

Tổng hợp lực là thay thế nhiều lực tác dụng đồng thời vào một vật bằng một lực có tác dụng giống hệt như tác dụng của toàn bộ những lực ấy.

Lực thay thế gọi là hợp lực.

Các lực được thay thế gọi là các lực thành phần.

* Hợp của 2 lực:

+ Hướng: Áp dụng quy tắc hình bình hành để tìm \(\overrightarrow F  = \overrightarrow {{F_1}}  + \overrightarrow {{F_2}} \):

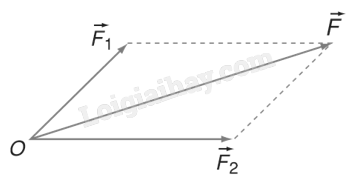
+ Độ lớn: \(F = \sqrt {{F_1}^2 + {F_2}^2 + 2{F_1}{F_2}\cos \left( {\overrightarrow {{F_1}} ,\overrightarrow {{F_2}} } \right)} \).

* Hợp của 3 lực:

+ Hướng: Áp dụng quy tắc hình bình hành để tìm \(\overrightarrow F  = \overrightarrow {{F_1}}  + \overrightarrow {{F_2}}  + \overrightarrow {{F_3}}  = \overrightarrow {{F_{12}}}  + \overrightarrow {{F_3}} \) (tương tự tổng hợp 2 lực).

+ Độ lớn: \(F = \sqrt {{F_1}^2 + {F_2}^2 + {F_3}^2 + 2{F_1}{F_2}\cos \left( {\overrightarrow {{F_1}} ,\overrightarrow {{F_2}} } \right) + 2{F_2}{F_3}\cos \left( {\overrightarrow {{F_2}} ,\overrightarrow {{F_3}} } \right) + 2{F_3}{F_1}\cos \left( {\overrightarrow {{F_3}} ,\overrightarrow {{F_1}} } \right)} \).

Ví dụ minh hoạ:

1) Có ba lực cùng tác động vào một cái bàn như hình vẽ. Trong đó hai lực \(\overrightarrow {{F_1}} \), \(\overrightarrow {{F_2}} \) có giá nằm trên mặt phẳng chứa mặt bàn, tạo với nhau một góc \({110^o}\) và có độ lớn lần lượt là 9N và 4N , lực \(\overrightarrow {{F_2}} \) vuông góc với mặt bàn và có độ lớn 7N. Độ lớn hợp lực của ba lực trên là a (N), tìm giá trị của a (kết quả quy tròn về số nguyên).

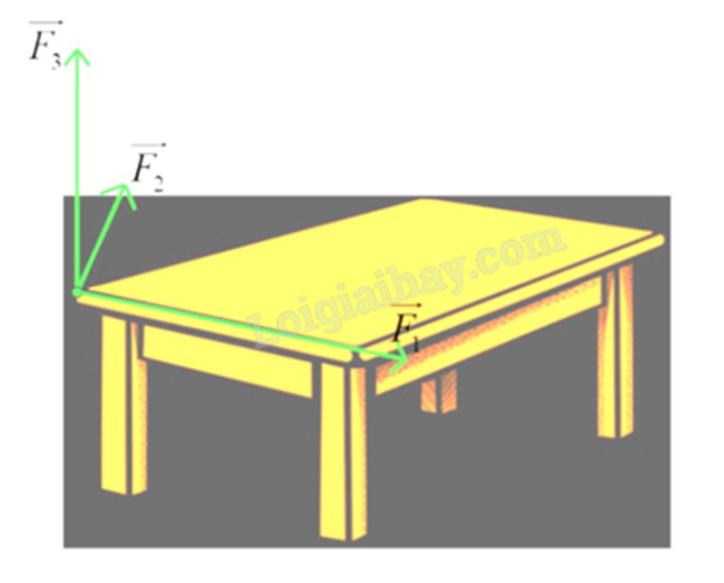
Giải:

\(\left| {\overrightarrow {{F_1}} + \overrightarrow {{F_2}} + \overrightarrow {{F_3}} } \right| = \sqrt {{{\left( {\overrightarrow {{F_1}} + \overrightarrow {{F_2}} + \overrightarrow {{F_3}} } \right)}^2}} \)

\( = \sqrt {{F_1}^2 + {F_2}^2 + {F_3}^2 + 2\overrightarrow {{F_1}} .\overrightarrow {{F_2}} + 2\overrightarrow {{F_2}} .\overrightarrow {{F_3}} + \overrightarrow {{F_3}} .\overrightarrow {{F_1}} } \)

\( = \sqrt {{F_1}^2 + {F_2}^2 + {F_3}^2 + 2{F_1}.{F_2}.\cos {{110}^o} + 2{F_2}.{F_3}.\cos {{90}^o} + 2{F_3}.{F_1}.\cos {{90}^o}} \)

\( = \sqrt {{9^2} + {4^2} + {7^2} + 2.9.4\cos {{110}^o} + 2.4.7.\cos {{90}^o} + 2.7.9.\cos {{90}^o}} \approx 11\) (N).

2) Ba lực \(\overrightarrow {{F_1}} \), \(\overrightarrow {{F_2}} \), \(\overrightarrow {{F_3}} \)​ cùng tác động vào một vật. Trong đó hai lực \(\overrightarrow {{F_1}} \), \(\overrightarrow {{F_2}} \) tạo với nhau một góc \({110^o}\) và có độ lớn lần lượt là 9 N, 4 N. Lực \(\overrightarrow {{F_3}} \) vuông góc với các lực \(\overrightarrow {{F_1}} \), \(\overrightarrow {{F_2}} \) và có độ lớn 7 N. Độ lớn hợp lực của ba lực trên là bao nhiêu Newton (N)? Kết quả làm tròn đến hàng đơn vị.

Giải:

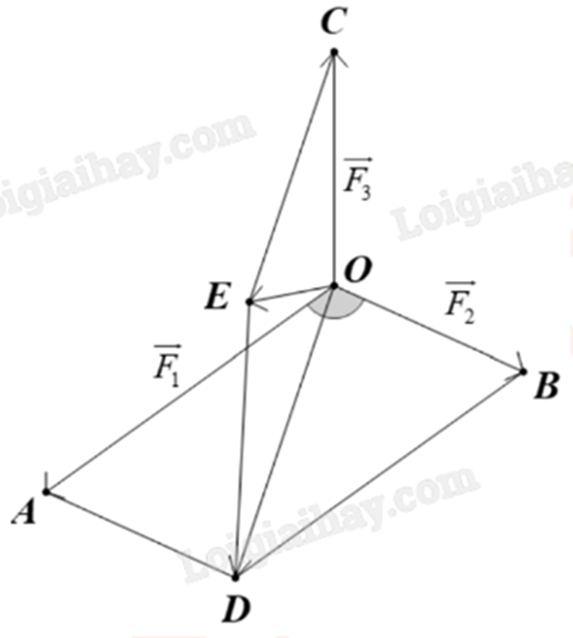
Giả sử các lực \(\overrightarrow {{F_1}} \), \(\overrightarrow {{F_2}} \), \(\overrightarrow {{F_3}} \)​ cùng tác động vào vật đặt tại điểm O.

Lấy các điểm A, B, C sao cho \(\overrightarrow {OA} = \overrightarrow {{F_1}} \), \(\overrightarrow {OB} = \overrightarrow {{F_2}} \), \(\overrightarrow {OC} = \overrightarrow {{F_3}} \).

Dựng các hình bình hành OADB và OCED như hình vẽ.

Hợp lực tác động vào vật là \(\vec F= \overrightarrow {OA} + \overrightarrow {OB} + \overrightarrow {OC} = \overrightarrow {OD} + \overrightarrow {OC} = \overrightarrow {OE} \) (quy tắc hình bình hành).

Xét hình bình hành OADB:

\(O{D^2} = O{A^2} + O{B^2} + 2.OA.OB.\cos \widehat {AOB}\)

\( = {9^2} + {4^2} + 2.9.4.\cos {110^o} = 97 + 72\cos {110^o}\).

Vì \(\overrightarrow {{F_3}} \) vuông góc với các lực \(\overrightarrow {{F_1}} \), \(\overrightarrow {{F_2}} \) nên OC vuông góc với OA và OB.

Khi đó, OC vuông góc với mặt phẳng (OADB), suy ra OC vuông góc với OD.

Suy ra OCED là hình chữ nhật.

\(OE = \sqrt {O{C^2} + C{E^2}} = \sqrt {O{C^2} + O{D^2}} = \sqrt {{7^2} + {{\left( {97 + 72\cos {{110}^o}} \right)}^2}} \approx 11\).

Vậy độ lớn hợp lực \(\vec F= \overrightarrow {OE} \) bằng 11 N.