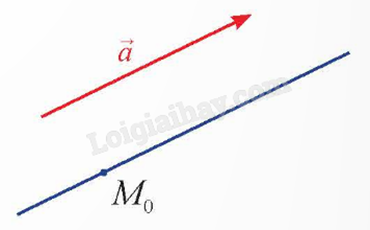
1. Vecto chỉ phương của đường thẳng
Vecto \(\overrightarrow a \ne \overrightarrow 0 \) có giá song song hoặc trùng với đường thẳng d được gọi là vecto chỉ phương của d.
2. Cách lập phương trình đường thẳng đi qua một điểm biết vecto chỉ phương trong không gian
Trong không gian Oxyz, cho đường thẳng d đi qua điểm \(M\left( {{x_0};{y_0};{z_0}} \right)\) và nhận \(\overrightarrow u = (a;b;c)\) làm vecto chỉ phương. Khi đó:
+ Phương trình chính tắc của d: \(\frac{{x - {x_0}}}{a} = \frac{{y - {y_0}}}{b} = \frac{{z - {z_0}}}{c}\) \(\left( {abc \ne 0} \right)\).
+ Phương trình tham số của d: \(\left\{ \begin{array}{l}x = {x_0} + at\\y = {y_0} + bt\\z = {z_0} + ct\end{array} \right.\) \((t \in \mathbb{R})\).
Ví dụ minh hoạ:
1) Phương trình của đường thẳng đi qua điểm M(1;-3;5) và có một vecto chỉ phương \(\vec u\left( {2; - 1;1} \right)\) là:
\(\frac{{x - 1}}{2} = \frac{{y + 3}}{{ - 1}} = \frac{{z - 5}}{1}\).
2) Đường thẳng đi qua điểm B(-1;3;6) nhận \(\vec u{\rm{\;}} = \left( {2; - 3;8} \right)\) làm vecto chỉ phương có phương trình chính tắc là:
\(\frac{{x - \left( { - 1} \right)}}{2} = \frac{{y - 3}}{{ - 3}} = \frac{{z - 6}}{8} \Leftrightarrow \frac{{x + 1}}{2} = \frac{{y - 3}}{{ - 3}} = \frac{{z - 6}}{8}\).
3) d đi qua điểm M(3;-1;4) có vecto chỉ phương \(\vec u{\rm{\;}} = ( - 2;4;5)\) có phương trình là \(\left\{ {\begin{array}{*{20}{c}}{x = 3 - 2t}\\{y = {\rm{\;}} - 1 + 4t}\\{z = 4 + 5t}\end{array}} \right.\) \((t \in \mathbb{R})\).
4) d đi qua điểm M(1;1;1) có vecto chỉ phương \(\vec u{\rm{\;}} = (2;3;4)\) có phương trình là \(\left\{ {\begin{array}{*{20}{l}}{x = 1 + 2t}\\{y = 1 + 3t}\\{z = 1 + 4t}\end{array}} \right.\) \((t \in \mathbb{R})\).

 Phương trình đường thẳng trong không gian - Từ điển Toá..
Phương trình đường thẳng trong không gian - Từ điển Toá.. 






Danh sách bình luận