Cho tam giác $ABC$ có $AB = AC$ và $MB = MC$ (\(M \in BC\)). Chọn câu sai.
-
A.
$\Delta AMC = \Delta BCM$
-
B.
$AM \bot BC$
-
C.
\(\widehat {BAM} = \widehat {CAM}\)
-
D.
\(\Delta AMB = \Delta AMC\)
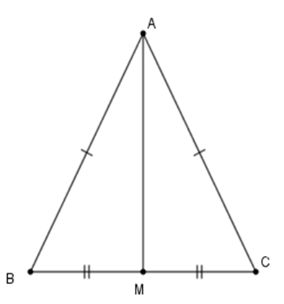
Xét \(\Delta AMB\) và \(\Delta AMC\) có
\(AB = AC\,\left( {gt} \right)\)
\(MB = MC\left( {gt} \right)\)
Cạnh \(AM\) chung
Nên \(\Delta AMB = \Delta AMC\,\left( {c - c - c} \right)\)
Suy ra \(\widehat {BAM} = \widehat {CAM}\) và $\widehat {AMB} = \widehat {AMC}$ (hai góc tương ứng bằng nhau) mà \(\widehat {AMB} + \widehat {AMC} = 180^\circ \) (hai góc kề bù)
Nên $\widehat {AMB} = \widehat {AMC} = \dfrac{{180^\circ }}{2} = 90^\circ .$ Hay \(AM \bot BC.\)
Vậy B, C, D đúng, A sai.
Đáp án : A

Các bài tập cùng chuyên đề
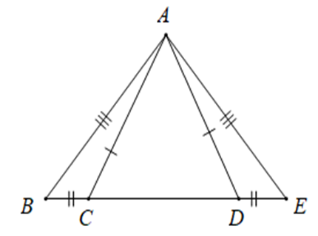
Cho hình vẽ sau. Tam giác nào bằng với tam giác \(ABC?\)
-
A.
\(\Delta ABC = \Delta {\rm E}DA\)
-
B.
\(\Delta ABC = \Delta EAD\)
-
C.
\(\Delta ABC = \Delta AED\)
-
D.
\(\Delta ABC = \Delta ADE\)
Cho hai tam giác $ABD$ và $CDB$ có cạnh chung $BD.$ Biết $AB = DC$ và $AD = CB.$ Phát biểu nào sau đây là sai:
-
A.
\(\Delta ABC = \Delta CDA\)
-
B.
\(\widehat {ABC} = \widehat {CDA}\)
-
C.
\(\widehat {BAC} = \widehat {DAC}\)
-
D.
\(\widehat {BCA} = \widehat {DAC}\)
Cho hình dưới đây.
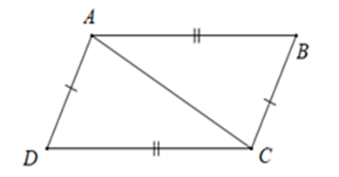
Chọn câu sai.
-
A.
\(AD//BC\)
-
B.
\(AB//CD\)
-
C.
\(\Delta ABC = \Delta CDA\)
-
D.
\(\Delta ABC = \Delta ADC\)
Cho đoạn thẳng \(AB = 6cm.\) Trên một nửa mặt hẳng bờ $AB$ vẽ tam giác $ABC$ sao cho \(AC = 4cm,\) \(BC = 5cm,\) trên nửa mặt phẳng còn lại vẽ tam giác $ABD$ sao cho \(BD = 4cm,\) \(AD = 5cm.\) Chọn câu đúng.
-
A.
\(\Delta CAB = \Delta DAB\)
-
B.
\(\Delta ABC = \Delta BDA\)
-
C.
\(\Delta CAB = \Delta DBA\)
-
D.
\({\rm{\Delta CAB = \Delta {\rm A}{\rm B}D}}\)
Cho tam giác $MNP$ có $MN = MP.$ Gọi $A$ là trung điểm của $NP.$ Biết \(\widehat {NMP} = {40^0}\) thì số đo góc $MPN$ là:
-
A.
\({100^0}\)
-
B.
\({70^0}\)
-
C.
\({80^0}\)
-
D.
\({90^0}\)
Cho tam giác $ABC$ có $AB < AC$ . Gọi \(E \in AC\) sao cho \(AB = CE\). Gọi $O$ là một điểm nằm ở trong tam giác sao cho $OA = OC,OB = OE.$ Khi đó:
-
A.
\(\Delta AOB = \Delta CEO\)
-
B.
\(\Delta AOB = \Delta COE\)
-
C.
\(\widehat {AOB} = \widehat {OEC}\)
-
D.
\(\widehat {ABO} = \widehat {OCE}\)
Cho \(\widehat {xOy} = {50^0}\), vẽ cung tròn tâm $O$ bán kính bằng $2cm,$ cung tròn này cắt $Ox, Oy$ lần lượt ở $A$ và $B.$ Vẽ các cung tròn tâm $A$ và tâm $B$ có bán kính $3cm,$ chúng cắt nhau tại điểm $C$ nằm trong góc $xOy.$ Tính \(\widehat {xOC}\) .
-
A.
\({25^0}\)
-
B.
\({50^0}\)
-
C.
\({80^0}\)
-
D.
\({90^0}\)






