Đề bài
Cho hình dưới đây.
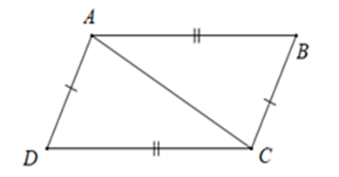
Chọn câu sai.
-
A.
\(AD//BC\)
-
B.
\(AB//CD\)
-
C.
\(\Delta ABC = \Delta CDA\)
-
D.
\(\Delta ABC = \Delta ADC\)
Phương pháp giải
Dựa vào trường hợp bằng nhau thứ nhất của tam giác cạnh-cạnh-cạnh.
Sử dụng dấu hiệu nhận biết hai đường thẳng song song.
Lời giải của GV Loigiaihay.com
Xét tam giác \(ADC\) và \(CBA\) có
$AB = CD$
$AD = BC$
$DB$ chung
$ \Rightarrow \Delta ADC = CBA\left( {c.c.c} \right)$
Do đó \(\widehat {DAC} = \widehat {BCA}\) (hai góc tương ứng) mà hai góc ở vị trí so le trong nên \(AD//BC.\)
Tương tự ta có \(AB//DC.\)
Vậy A, B, C đúng, D sai.
Đáp án : D







