Bài 3. Gia tốc và đồ thị vận tốc - thời gian trang 28, 29, 30, 31, 32 Vật Lí 10 Cánh diều
Một ô tô tăng tốc từ lúc đứng yên, sau 6,0 s đạt vận tốc 18 m/s. Tính độ lớn gia tốc của ô tô. Người lái xe ô tô hãm phanh để xe giảm tốc độ từ 23 m/s đến 11 m/s trong 20 s. Một người lái ô tô đang đi với tốc độ ổn định trên đường cao tốc, chợt nhìn thấy tín. Từ độ dốc của đồ thị vận tốc – thời gian của chuyển động thẳng. Bảng 1.2 liệt kê một số giá trị vậ tốc của người đi xe máy trong quá trình tốc độ dọc.
Câu hỏi tr 29 CH 1
Một ô tô tăng tốc từ lúc đứng yên, sau 6,0 s đạt vận tốc 18 m/s. Tính độ lớn gia tốc của ô tô
Phương pháp giải:
Biểu thức tính độ lớn của gia tốc: \(a = \frac{{\Delta v}}{{\Delta t}}\)
Trong đó:
+ \(\Delta v\): độ thay đổi vận tốc (m/s); \(\Delta v = \left| {{v_2} - {v_1}} \right|\)
+ \(\Delta t\): thời gian (s)
+ a: gia tốc (m/s2 )
Lời giải chi tiết:
Gia tốc của ô tô là:
\(a = \frac{{\Delta v}}{{\Delta t}} = \frac{{18 - 0}}{6} = 3(m/{s^2})\)
Câu hỏi tr 29 CH 2
Người lái xe ô tô hãm phanh để xe giảm tốc độ từ 23 m/s đến 11 m/s trong 20 s. Tính độ lớn của gia tốc.
Phương pháp giải:
Biểu thức tính độ lớn của gia tốc: \(a = \frac{{\Delta v}}{{\Delta t}}\)
Trong đó:
+ \(\Delta v\): độ thay đổi vận tốc (m/s); \(\Delta v = \left| {{v_2} - {v_1}} \right|\)
+ \(\Delta t\): thời gian (s)
+ a: gia tốc (m/s2 )
Lời giải chi tiết:
Gia tốc của ô tô là:
\(a = \frac{{\Delta v}}{{\Delta t}} = \frac{{\left| {11 - 23} \right|}}{{20}} = 0,6(m/{s^2})\)
Câu hỏi tr 29 CH 3
Trong một cuộc thi chạy, từ trạng thái đứng yên, một vận động viên chạy với gia tốc 5,0 m/s2 trong 2,0 giây đầu tiên. Tính vận tốc của vận động viên sau 2,0 s.
Phương pháp giải:
Biểu thức tính độ thay đổi vận tốc:
\(\Delta v = a.\Delta t\)
Trong đó:
+ \(\Delta v\): độ thay đổi vận tốc (m/s); \(\Delta v = \left| {{v_2} - {v_1}} \right|\)
+ \(\Delta t\): thời gian (s)
+ a: gia tốc (m/s2 )
Lời giải chi tiết:
Ta có:
a = 5 m/s2
\(\Delta t = 2\)s
v1 = 0 m/s
Độ thay đổi vận tốc của vận động viên là:
\(\Delta v = a.\Delta t = 5.2 = 10(m/s)\)
=> Vận tốc của vận động viên sau 2 s là: 10 – 0 = 10 m/s
Câu hỏi tr 30 CH 1
Một người lái ô tô đang đi với tốc độ ổn định trên đường cao tốc, chợt nhìn thấy tín hiệu báo có nguy hiểm ở phía trước nên dần dần giảm tốc độ. Ô tô tiến thêm một đoạn thì người này thấy một tai nạn đã xảy ra và phanh gấp để dừng lại. Vẽ phác đồ thị vận tốc – thời gian để biểu diễn chuyển động của ô tô này.
Phương pháp giải:
Vận dụng kiến thức đã học
Lời giải chi tiết:
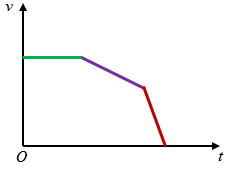
Câu hỏi tr 30 CH 2
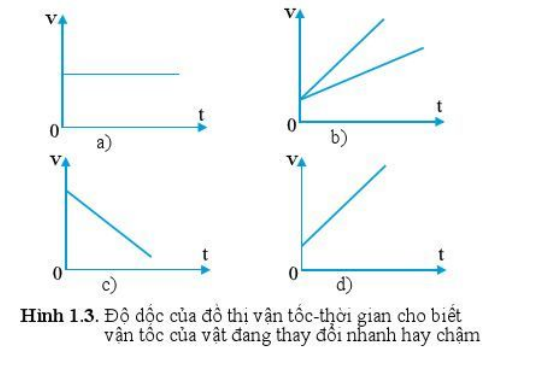
Từ độ dốc của đồ thị vận tốc – thời gian của chuyển động thẳng trên hình 1.3, hình nào tương ứng với mỗi phát biểu sau đây?
1. Độ dốc dương, gia tốc không đổi.
2. Độ dốc lớn hơn, gia tốc lớn hơn.
3. Độ dốc bằng không, gia tốc a = 0.
4. Độ dốc âm, gia tốc âm (chuyển động chậm dần).
Phương pháp giải:
Quan sát hình vẽ
Lời giải chi tiết:
1 – d
2 – b
3 – a
4 – c
Câu hỏi tr 31
Bảng 1.2 liệt kê một số giá trị vận tốc của người đi xe máy trong quá trình tốc độ dọc theo một con đường thẳng.
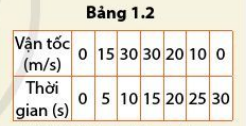
a) Vẽ đồ thị vận tốc – thời gian cho chuyển động này.
b) Từ những số đo trong bảng, hãy suy nghĩ gia tốc của người đi xe máy trong 10 s đầu tiên.
c) Kiểm tra kết quả tính được của bạn bằng cách tìm độ dốc của đồ thị trong 10 s đầu tiên.
d) Xác định gia tốc của người đi xe máy trong thời gian 15 s cuối cùng.
e) Sử dụng đồ thị để tìm tổng quãng đường đã đi trong quá trình thử tốc độ.
Phương pháp giải:
- Biểu thức tính gia tốc:
\(a = \frac{{\Delta v}}{{\Delta t}}\)
Trong đó:
+ \(\Delta v\): độ thay đổi vận tốc (m/s); \(\Delta v = \left| {{v_2} - {v_1}} \right|\)
+ \(\Delta t\): thời gian (s)
+ a: gia tốc (m/s2 )
- Độ dốc của đồ thị vận tốc - thời gian = gia tốc của chuyển động
Lời giải chi tiết:
a)
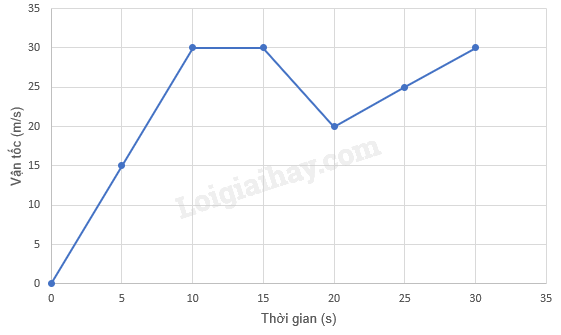
b)
Trong 10 s đầu tiên, ta có:
+ \(\Delta v = 30(m/s)\)
+ \(\Delta t = 10(s)\)
=> Gia tốc của người đi xe máy trong 10 s đầu tiên là:
\(a = \frac{{\Delta v}}{{\Delta t}} = \frac{{30}}{{10}} = 3(m/{s^2})\)
c) Từ đồ thị ta có:
+ \(\Delta v = 30(m/s)\)
+ \(\Delta t = 10(s)\)
=> Độ dốc của người đi xe máy trong 10 s đầu tiên là:
\(a = \frac{{\Delta v}}{{\Delta t}} = \frac{{30}}{{10}} = 3(m/{s^2})\)
d) Trong 15 s cuối cùng, ta có:
+ \(\Delta v = 30(m/s)\)
+ \(\Delta t = 15(s)\)
=> Gia tốc của người đi xe máy trong 15 s cuối cùng là:
\(a = \frac{{\Delta v}}{{\Delta t}} = \frac{{30}}{{15}} = 2(m/{s^2})\)
e) Do vật không đổi chiều chuyển động nên độ dịch chuyển = quãng đường đi được = Diện tích đồ thị
+ Từ 0 - 10 s, quãng đường vật đi được là: \({S_1} = \frac{1}{2}.10.30 = 150(m)\)
+ Từ 10 - 15 s, quãng đường vật đi được là: \({S_2} = 30.5 = 150(m)\)
+ Từ 15 s - 20 s, quãng đường vật đi được là: \({S_3} = \frac{{(30 + 20).5}}{2} = 125(m)\)
+ Từ 20 s - 30 s, quãng đường vật đi được là: \({S_4} = \frac{{(30 + 20).10}}{2} = 250(m)\)
=> Tổng quãng đường vật đi được là: S = 150 + 150 + 125 + 250 = 675 (m).
Chú ý:
+ Diện tích hình tam giác: S = 1/2. đáy. chiều cao
+ Diện tích hình chữ nhật: S = chiều dài . chiều rộng
+ Diện tích hình thang: S = (đáy lớn + đáy bé) . chiều cao / 2
- Bài 4. Chuyển động biến đổi trang 33, 34, 35, 36, 37, 38, 39, 40, 41 Vật Lí 10 Cánh diều
- Bài tập chủ đề 1_2 trang 42 Vật Lí 10 Cánh diều
- Bài tập chủ đề 1 trang 27 Vật Lí 10 Cánh diều
- Bài 2. Đồ thị độ dịch chuyển - thời gian. Độ dịch chuyển tổng hợp và vận tốc tổng hợp trang 21, 22, 23, 24, 25, 26 Vật Lí 10 Cánh diều
- Bài 1. Tốc độ, độ dịch chuyển và vận tốc trang 15, 16, 17, 18, 19, 20 Vật Lí 10 Cánh diều
>> Xem thêm
Các bài khác cùng chuyên mục













Danh sách bình luận