Giải bài 7 trang 76 sách bài tập toán 11 - Chân trời sáng tạo tập 2

Cho hình hộp đứng ABCD.A’B’C’D’ có đáy ABCD là hình thoi cạnh 2a. Mặt phẳng (B’AC) tạo với đáy một góc ${30^0}$ , khoảng cách từ B đến mặt phẳng (D’AC) bằng $\frac{a}{2}$ . Tính thể tích khối tứ diện ACB’D’.

Tổng hợp đề thi học kì 2 lớp 11 tất cả các môn - Chân trời sáng tạo

Toán - Văn - Anh - Lí - Hóa - Sinh

Đề bài

Cho hình hộp đứng ABCD.A’B’C’D’ có đáy ABCD là hình thoi cạnh 2a. Mặt phẳng (B’AC) tạo với đáy một góc ${30^0}$ , khoảng cách từ B đến mặt phẳng (D’AC) bằng $\frac{a}{2}$ . Tính thể tích khối tứ diện ACB’D’.

Phương pháp giải - Xem chi tiết

+ Sử dụng kiến thức về góc giữa hai mặt phẳng để tính: Góc giữa hai mặt phẳng cắt nhau bằng góc giữa hai đường thẳng lần lượt nằm trong hai mặt phẳng và vuông góc với giao tuyến của hai mặt phẳng.

+ Sử dụng kiến thức về thể tích khối tứ diện.

Quảng cáo

Lời giải chi tiết

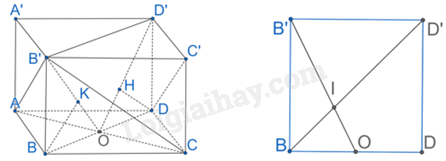
Gọi O là giao điểm của AC và BD.

Ta có: $AC \bot BD,AC \bot BB'$ $\Rightarrow AC \bot \left( {BB'D} \right)$ $\Rightarrow AC \bot B'O$

Khi đó, $BO \bot AC,B'O \bot AC,BO \subset \left( {ABCD} \right),B'O \subset \left( {B'AC} \right)$ , AC là giao tuyến của (B’AC) và (ABCD). Do đó, $\left( {\left( {B'AC} \right),\left( {ABCD} \right)} \right) = \left( {BO,B'O} \right) = \widehat {B'OB} = {30^0}$

Ta có: $d\left( {B,\left( {D'AC} \right)} \right) = d\left( {D,\left( {D'AC} \right)} \right) = \frac{a}{2}$

Chứng minh được: $AC \bot \left( {BB'D'D} \right)$ $\Rightarrow \left( {D'AC} \right) \bot \left( {BB'D'D} \right)$ và D’O là giao tuyến của (D’AC) và (BB’D’D).

Từ D kẻ $DH \bot D'O\left( {H \in D'O} \right)$ . Do đó, $d\left( {D,\left( {D'AC} \right)} \right) = DH = \frac{a}{2}$

Xét tam giác B’OB vuông tại B có: $\frac{{BB'}}{{BO}} = \tan {30^0}$ $\Rightarrow OD = BO = \sqrt 3 BB'$

Xét tam giác D’DO vuông tại D, đường cao DH có:

$\frac{1}{{D{H^2}}} = \frac{1}{{O{D^2}}} + \frac{1}{{D'{D^2}}}$ $\Rightarrow \frac{4}{{{a^2}}} = \frac{1}{{3BB{'^2}}} + \frac{1}{{D'{D^2}}}$ $\Rightarrow D'D = \frac{{a\sqrt 3 }}{3}$ $\Rightarrow OB = a$

Gọi I là giao điểm của BD’ và B’O, suy ra: $\frac{{BI}}{{D'I}} = \frac{1}{2}$ $\Rightarrow d\left( {D',\left( {B'AC} \right)} \right) = 2d\left( {B,\left( {B'AC} \right)} \right)$ $\Rightarrow {V_{ACB'D'}} = 2{V_{B'ABC}}$

Tam giác AOB vuông tại O có: $OA = \sqrt {A{B^2} - O{B^2}} = \sqrt {4{a^2} - {a^2}} = a\sqrt 3$

Diện tích tam giác ABC là: ${S_{ABC}} = 2{S_{ABO}} = 2.\frac{1}{2}.OB.OA = {a^2}\sqrt 3$

Suy ra: ${V_{B'ABC}} = \frac{1}{3}BB'.{S_{ABC}} = \frac{1}{3}.\frac{{a\sqrt 3 }}{3}.{a^2}\sqrt 3 = \frac{{{a^3}}}{3}$ . Vậy ${V_{ACB'D'}} = \frac{{2{a^3}}}{3}$

Bình luận

Chia sẻ

Bình chọn:

4.9 trên 7 phiếu

Bài tiếp theo

Giải bài 8 trang 76 sách bài tập toán 11 - Chân trời sáng tạo tập 2
Một thùng đựng rác có dạng hình chóp cụt tứ giác đều. Đáy và miệng thùng có độ dài lần lượt là 60cm và 120cm, cạnh bên của thùng dài 100cm. Tính thể tích của thùng.
Giải bài 6 trang 76 sách bài tập toán 11 - Chân trời sáng tạo tập 2
Cho khối lăng trụ đứng ABC.A’B’C’ có đáy ABC là tam giác cân với $AB = AC = a,\widehat {BAC} = {120^0}$ ,
Giải bài 5 trang 76 sách bài tập toán 11 - Chân trời sáng tạo tập 2
Cho hình lăng trụ đứng ABC.A’B’C’ có đáy ABC là tam giác vuông tại B. Biết $AB = a,BC = a\sqrt 3$ ,
Giải bài 4 trang 76 sách bài tập toán 11 - Chân trời sáng tạo tập 2
Cho khối chóp S.ABC có $SA \bot \left( {ABC} \right)$ , tam giác ABC có độ dài 3 cạnh là $AB = 5a,BC = 8a,AC = 7a$ , góc giữa SB và (ABC) là ${45^0}$ . Tính thể tích khối chóp S.ABC.
Giải bài 3 trang 76 sách bài tập toán 11 - Chân trời sáng tạo tập 2
Cho hình chóp S. ABC có đáy là tam giác đều cạnh a. Hình chiếu vuông góc của S trên mặt phẳng (ABC) là điểm H thuộc cạnh AB sao cho $HA = 2HB$ .
Giải bài 2 trang 76 sách bài tập toán 11 - Chân trời sáng tạo tập 2
Cho tứ diện ABCD có hai mặt phẳng (ABC) và (ABD) cùng vuông góc với (DBC). a) Chứng minh hai mặt phẳng (ABE) và (DFK) cùng vuông góc với (ADC). b) Gọi O và H là trực tâm $\Delta BCD$ và $\Delta ACD$ .
Giải bài 1 trang 76 sách bài tập toán 11 - Chân trời sáng tạo tập 2
Cho tứ diện OABC có OA, OB, OC đôi một vuông góc với nhau. a) $BC \bot \left( {OAH} \right)$ . b) H là trực tâm của $\Delta ABC$ . c) $\frac{1}{{O{H^2}}} = \frac{1}{{O{A^2}}} + \frac{1}{{O{B^2}}} + \frac{1}{{O{C^2}}}$ .
Giải câu hỏi trắc nghiệm trang 74, 75 sách bài tập toán 11 - Chân trời sáng tạo tập 2
Trong không gian, khẳng định nào sau đây đúng? A. Cho hai đường thẳng song song, B. Trong không gian, C. Hai đường thẳng phân biệt vuông góc với nhau thì chúng cắt nhau. D. Hai đường thẳng phân biệt cùng vuông góc với đường thẳng thứ ba

>> Xem thêm

Luyện Bài Tập Trắc nghiệm Toán 11 - Chân trời sáng tạo - Xem ngay

Báo lỗi - Góp ý

Group 2K8 ôn Thi ĐGNL & ĐGTD Miễn Phí

>> 2K8! chú ý! Mở đặt chỗ Lộ trình Sun 2026: Luyện thi chuyên sâu TN THPT, Đánh giá năng lực, Đánh giá tư duy tại Tuyensinh247.com (Xem ngay lộ trình). Ưu đãi -70% (chỉ trong tháng 3/2025) - Tặng miễn phí khoá học tổng ôn lớp 11, 2K8 xuất phát sớm, X2 cơ hội đỗ đại học. Học thử miễn phí ngay.