Giải SBT đại số, hình học toán lớp 9 tập 1, tập 2 Bài 1. Một số hệ thức về cạnh và đường cao trong tam gi..

Bài 13 trang 104 SBT toán 9 tập 1


Giải bài 13 trang 104 sách bài tập toán 9. Cho hai đoạn thẳng có độ dài là a và b. Dựng các đoạn thẳng có độ dài tương ứng bằng:....

Tổng hợp Đề thi vào 10 có đáp án và lời giải

Toán - Văn - Anh

Lựa chọn câu để xem lời giải nhanh hơn

Cho hai đoạn thẳng có độ dài là \(a\) và \(b\). Dựng các đoạn thẳng có độ dài tương ứng bằng:

LG a

\(\sqrt {{a^2} + {b^2}}\)        

Phương pháp giải:

Áp dụng định lí Pytago vào tam giác OAB vuông tại O, ta có:

\(A{B^2} = O{A^2} + O{B^2}\)

Lời giải chi tiết:

\(\sqrt {{a^2} + {b^2}}\) 

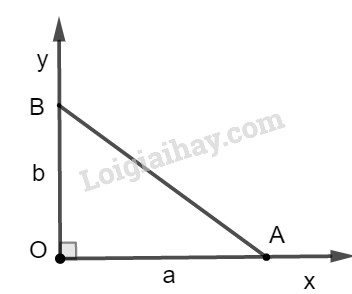
* Cách dựng:

−  Dựng góc vuông \(xOy\).

−  Trên tia \(Ox\), dựng đoạn \(OA = a\).

−  Trên tia \(Oy\), dựng đoạn \(OB = b\).

−  Nối \(AB\) ta có đoạn \(AB = \sqrt {{a^2} + {b^2}} \) cần dựng.

* Chứng minh:

Áp dụng định lý Pytago vào tam giác vuông \(AOB\), ta có:

\(A{B^2} = O{A^2} + O{B^2}\)\( = {a^2} + {b^2}\) 

Suy ra: \(AB = \sqrt {{a^2} + {b^2}}.\)

LG b

\(\sqrt {{a^2} - {b^2}} \,,\,\left( {a > b} \right)\) 

Phương pháp giải:

Áp dụng định lí Pytago vào tam giác OAB vuông tại O, ta có:

\(A{B^2} = O{A^2} + O{B^2}\)

Lời giải chi tiết:

\(\sqrt {{a^2} - {b^2}} \,,\,\left( {a > b} \right)\) 

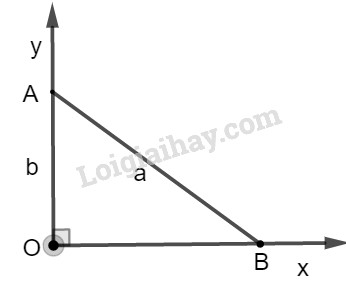
*  Cách dựng :

− Dựng góc vuông \(xOy\).

− Trên tia \(Oy\), dựng đoạn \(OA = b\).

− Dựng cung tròn tâm \(A\), bán kính bằng \(a\) cắt tia \(Ox\) tại \(B\).

Ta có đoạn \(OB = \sqrt {{a^2} - {b^2}} (a > b)\) cần dựng.

*     Chứng minh;

Áp dụng định lí Pytago vào tam giác vuông \(AOB\), ta có:

\(A{B^2} = O{A^2} + O{B^2} \Rightarrow O{B^2} \)\(= A{B^2} - O{A^2} = {a^2} - {b^2}\) 

Suy ra: \(OB = \sqrt {{a^2} - {b^2}} \)

Loigiaihay.com


Bình chọn:
4.4 trên 10 phiếu
Bài tiếp theo

>> Xem thêm

Luyện Bài Tập Trắc nghiệm Toán 9 - Xem ngay

Báo lỗi - Góp ý

Tham Gia Group 2K10 Ôn Thi Vào Lớp 10 Miễn Phí

Các bài khác cùng chuyên mục


App Loigiaihay trên google play store App Loigiaihay trên apple store

Hãy viết chi tiết giúp Loigiaihay.com

Vui lòng để lại thông tin để ad có thể liên hệ với em nhé!

Vấn đề em gặp phải là gì ?

Hãy viết chi tiết giúp Loigiaihay.com

Cảm ơn bạn đã sử dụng Loigiaihay.com. Đội ngũ giáo viên cần cải thiện điều gì để bạn cho bài viết này 5* vậy?

Vui lòng để lại thông tin để ad có thể liên hệ với em nhé!

Copyright © 2021 loigiaihay.com

DMCA.com Protection Status
App Loigiaihay trên apple store App Loigiaihay trên google play store