1. Khái niệm phương trình bậc nhất hai ẩn
Phương trình bậc nhất hai ẩn x và y là hệ thức dạng
\(ax + by = c\)
trong đó a, b và c là các số đã biết (\(a \ne 0\) hoặc \(b \ne 0\)).
2. Cách giải hệ phương trình bậc nhất hai ẩn bằng phần mềm GeoGebra
Để giải hệ hai phương trình bậc nhất hai ẩn, ta có thể sử dụng một trong hai phương pháp sau:
Cách 1. Sử dụng câu lệnh Solve({phương trình thứ nhất>, <phương trình thứ hai>}, (<biến số thứ nhất>, <biến số thứ hai>}) trên ô lệnh của cửa sổ CAS, kết quả sẽ được hiển thị ngay bên dưới.
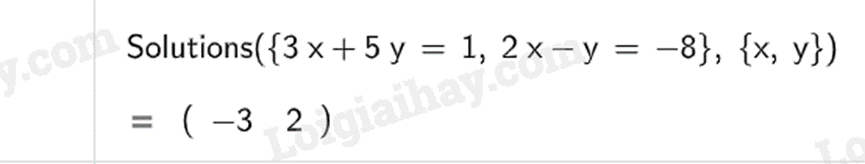
Kết quả của hệ phương trình có nghĩa: hệ có nghiệm \(\left\{ \begin{array}{l}x = - 3\\y = 2\end{array} \right.\).
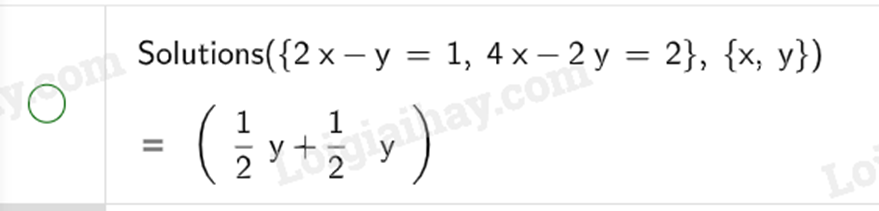
Kết quả của hệ phương trình có nghĩa: hệ có nghiệm \(\left\{ \begin{align} x=\frac{1}{2}y+\frac{1}{2} \\ y\,\text{tuỳ ý}\text{.} \end{align} \right.\)

Cách 2. Sử dụng lệnh Intersect (<phương trình thứ nhất>, <phương trình thứ hai>) trên cửa sổ CAS để tìm toạ độ giao điểm của hai đường thẳng có phương trình tương ứng.
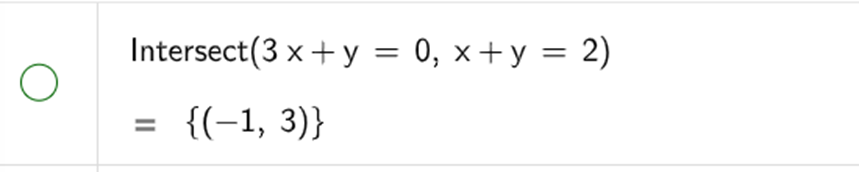

 Thực hành phần mềm Geogebra - Từ điển môn Toán 9
Thực hành phần mềm Geogebra - Từ điển môn Toán 9 





