1. Khái niệm hàm số y = ax²
Hàm số y = ax2, là một dạng của hàm số bậc hai, là hàm số có dạng như sau: \(y = a{x^2}\left( {a \ne 0} \right)\)
Hàm số \(y = a{x^2}\left( {a \ne 0} \right)\) xác định với mọi giá trị x thuộc \(\mathbb{R}\).
Ví dụ: Hàm số \(y = 2{x^2},y = - \frac{3}{2}{x^2}\) là các hàm số có dạng \(y = a{x^2}\left( {a \ne 0} \right)\).
2. Khái niệm đồ thị của hàm số y = ax² (a ≠ 0)
Đồ thị của hàm số \(y = a{x^2}\left( {a \ne 0} \right)\) là một đường cong được gọi là parabol. Parabol đó luôn đi qua gốc toạ độ và có dạng như sau:
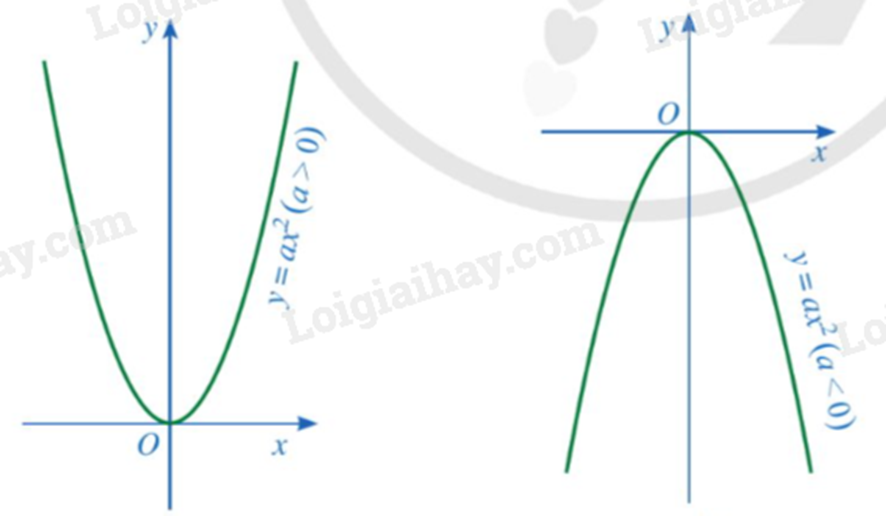
3. Cách vẽ đồ thị của hàm số bằng phần mềm GeoGebra
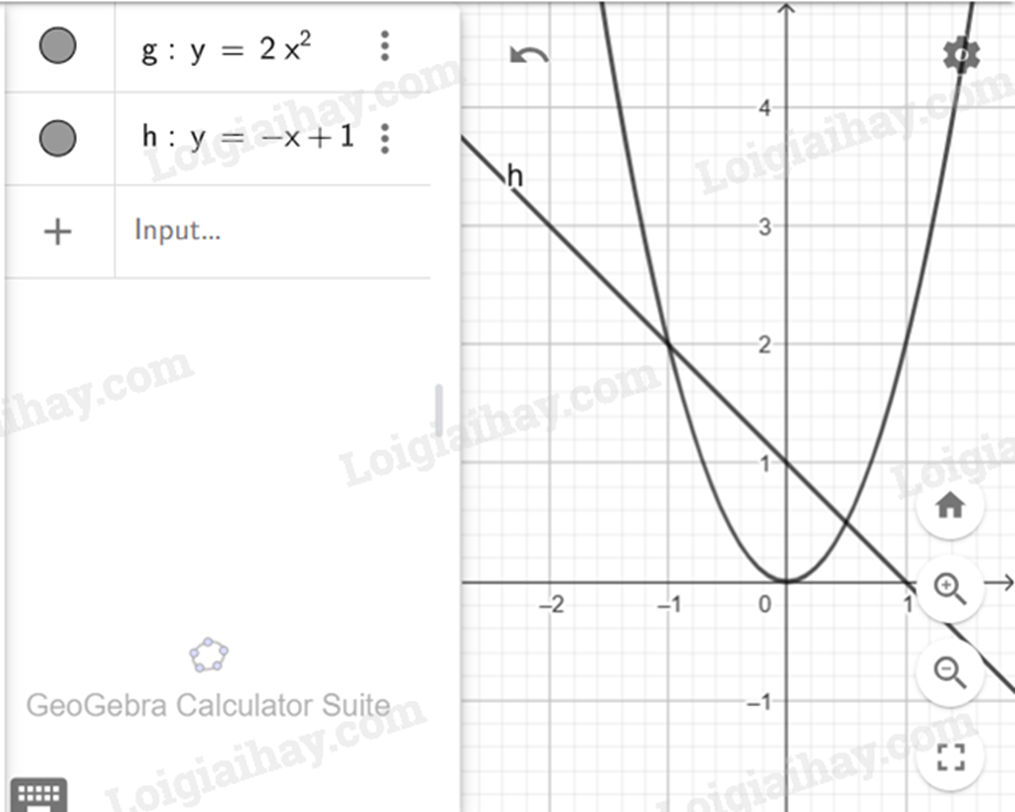
Khởi động GeoGebra và chọn đồng thời hai chế độ Graphic 2 và CAS để vẽ đồ thị của hàm số \(y = a{x^2}\left( {a \ne 0} \right)\) và hàm số bậc nhất \(y = ax + b\left( {a \ne 0} \right)\).
- Nhập công thức hàm số \(y = a{x^2}\) và \(y = ax + b\) vào từng ô lệnh trong cửa số CAS.
- Nháy chuột chọn nút  ở đầu mỗi ô lệnh để vẽ đồ thị hàm số trong cửa sổ Graphic 2.
ở đầu mỗi ô lệnh để vẽ đồ thị hàm số trong cửa sổ Graphic 2.
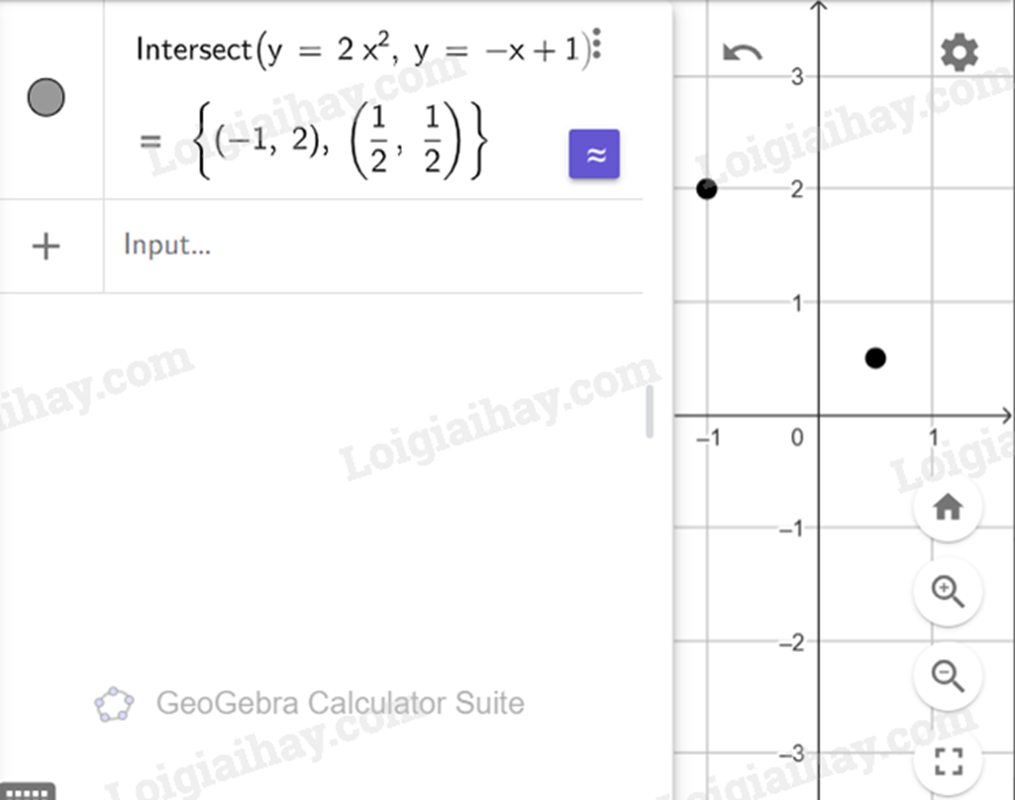
- Sử dụng lệnh Intersect (<hàm số thứ nhất>, <hàm số thứ hai>) trên cửa sổ CAS. Toạ độ các giao điểm của hai đồ thị hàm số sẽ hiển thị bên dưới ở dạng tập hợp.
Chú ý: Nếu muốn sử dụng giao diện tiếng Việt, sau khi khởi động GeoGebra, chọn Options → Language → Vietnamese/Tiếng Việt. Khi đó, thay vì cú pháp lệnh tiếp Anh như trình bày ở trên, ta dùng cú pháp lệnh tiếng Việt tương ứng như trong bảng sau (lưu ý rằng cú pháp lệnh tiếng Việt có thể khác nhau tuỳ theo phiên bản GeoGebra).
|
Lệnh |
Cú pháp lệnh tiếng Anh |
Cú pháp lệnh tiếng Việt |
|
Giải phương trình |
Solve(<phương trình>) |
Giai(<phương trình>) |
|
Solutions(<phương trình>) |
CacNghiem(<phương trình>) |
|
|
Giải hệ phương trình |
Solve({phương trình thứ nhất>, <phương trình thứ hai>}, (<biến số thứ nhất>, <biến số thứ hai>}) |
Giai({phương trình thứ nhất>, <phương trình thứ hai>}, (<biến số thứ nhất>, <biến số thứ hai>}) |
|
Solutions({phương trình thứ nhất>, <phương trình thứ hai>}, (<biến số thứ nhất>, <biến số thứ hai>}) |
CacNghiem({phương trình thứ nhất>, <phương trình thứ hai>}, (<biến số thứ nhất>, <biến số thứ hai>}) |
|
|
Tìm giao điểm của hai đồ thị |
Intersect (<hàm số thứ nhất>, <hàm số thứ hai>) |
GiaoDiem (<hàm số thứ nhất>, <hàm số thứ hai>) |

 Thực hành phần mềm Geogebra - Từ điển môn Toán 9
Thực hành phần mềm Geogebra - Từ điển môn Toán 9 





