Bài 1. Đường thẳng và mặt phẳng trong không gian Toán 1..

Bài 4.4 trang 94 SGK Toán 11 tập 1 - Cùng khám phá

Trong mặt phẳng (P), cho tứ giác ABCD. Gọi S là điểm không thuộc mặt phẳng (P). Lấy M, N lần lượt là trung điểm của các đoạn thẳng SA, SC.

Đề bài

Trong mặt phẳng (P), cho tứ giác ABCD. Gọi S là điểm không thuộc mặt phẳng (P). Lấy M, N lần lượt là trung điểm của các đoạn thẳng SA, SC.

a) Xác định giao điểm K của đường thẳng SD và mặt phẳng (BMN).

b) Gọi P là giao điểm của hai đường thẳng MK và AD, Q là giao điểm của hai đường thẳng NK và CD. Chứng minh rằng ba diểm P, Q, B thằng hàng.

Phương pháp giải - Xem chi tiết

a) Tìm giao điểm của đường thẳng d và mặt phẳng (P)

Cách 1: Nếu (P) có chứa đường thẳng cắt d

\(\left\{ \begin{array}{l}a \subset \left( P \right)\\a \cap d = I\end{array} \right. \Rightarrow I = d \cap \left( P \right)\)

Cách 2: Nếu (P) không chứa đường thẳng cắt d

+ Bước 1: Tìm \(\left( Q \right) \supset d\) và \(\left( P \right) \cap \left( Q \right) = a\)

+ Bước 2: Tìm \(I = a \cap d \Rightarrow I = d \cap \left( P \right)\)

b) P, Q, B cùng thuộc 2 mặt phẳng phân biệt thì P, Q, B thẳng hàng.

Lời giải chi tiết

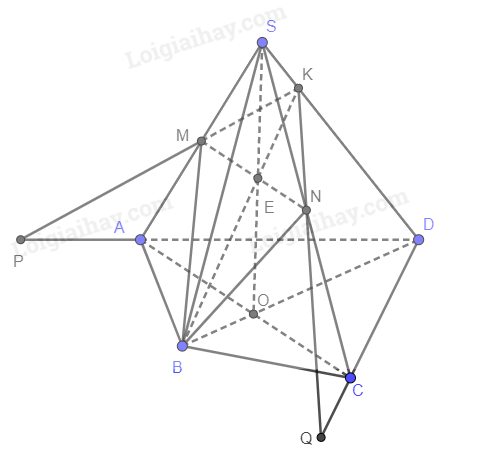
a) Trong (ABCD), gọi \(AC \cap BD = O\)

Trong (SAC), gọi \(SO \cap MN = E\)

\(\left\{ \begin{array}{l}BE \cap SD = K\\BE \subset \left( {BMN} \right)\end{array} \right. \Rightarrow K = SD \cap \left( {BMN} \right)\)

b) Theo phần a, K thuộc (BMN) nên mở rộng (BMN) thành (BMKN)

\(\begin{array}{l}\left\{ \begin{array}{l}MK \cap AD = P\\MK \subset \left( {BMNK} \right)\\AD \subset \left( {ABCD} \right)\end{array} \right. \Rightarrow P \in \left( {BMNK} \right) \cap \left( {ABCD} \right)\\\left\{ \begin{array}{l}NK \cap CD = Q\\NK \subset \left( {BMNK} \right)\\CD \subset \left( {ABCD} \right)\end{array} \right. \Rightarrow Q \in \left( {BMNK} \right) \cap \left( {ABCD} \right)\end{array}\)

\( \Rightarrow P,Q \in \left( {BMN} \right) \cap \left( {ABCD} \right)\)

Mà: \(B \in \left( {BMN} \right) \cap \left( {ABCD} \right)\)

Vậy P, B, Q thẳng hàng.

Bình luận

Chia sẻ

Bình chọn:

4.9 trên 7 phiếu

Bài tiếp theo

Bài 4.5 trang 94 SGK Toán 11 tập 1 - Cùng khám phá
Có tồn tại hay không một hình chóp có số cạnh (gồm cả cạnh bên và cạnh đáy) của nó là số lẻ? Vì sao?
Bài 4.6 trang 94 SGK Toán 11 tập 1 - Cùng khám phá
Cho hình chóp S.ABCD có đáy là hình bình hành ABCD. Gọi G là trọng tâm của tam giác SCD.
Bài 4.3 trang 94 SGK Toán 11 tập 1 - Cùng khám phá
Cho bốn điểm không đồng phẳng A, B, C, D. Gọi M, N lần lượt là trung điểm của các đoạn thẳng AB, CD.
Bài 4.2 trang 94 SGK Toán 11 tập 1 - Cùng khám phá
Trong mặt phẳng (P), cho hình bình hành ABCD. Lấy S nằm ngoài mặt phẳng (P). Lấy M, N lần lượt là các điểm nằm trên các cạnh SA, SC.
Bài 4.1 trang 94 SGK Toán 11 tập 1 - Cùng khám phá
Thả diều là một trong những trò chơi dân gian được nhiều bạn nhỏ yêu thích. Để tự thiết kế một cánh diều từ giấy và thanh tre có nhiều cách khác nhau, nhưng trong trường hợp đơn giản nhất, người ta thường dùng hai thanh tre nẹp vào giấy và buộc nút thắt như Hình 4.37. Hai thanh tre này có tác dụng gì?
Giải mục 3 trang 90, 91, 92, 93 SGK Toán 11 tập 1 - Cùng khám phá
Bánh ít lá gai là một đặc sản của người miền Trung, có dạng là một hình chóp tứ giác như Hình 4.29a.
Giải mục 2 trang 85, 86, 87, 88, 89, 90 SGK Toán 11 tập 1 - Cùng khám phá
Trong hình học phẳng, qua hai điểm phân biệt có thể xác định được bao nhiêu đường thẳng?
Giải mục 1 trang 83, 84 SGK Toán 11 tập 1 - Cùng khám phá
Đây là hình ảnh bên trong một phòng học. Hãy chỉ ra các vật có bề mặt phẳng, nhẵn.
Lý thuyết Đường thẳng và mặt phẳng trong không gian - SGK Toán 11 Cùng khám phá
I. Khái niệm mở đầu