Giải bài tập Tài liệu Dạy - học Toán lớp 7, Phát triển tư duy đột phá trong dạy học Toán 7 Bài tập - Chủ đề 4: Tam giác cân. Định lý Pythagore

Bài 15 trang 170 Tài liệu dạy – học Toán 7 tập 1


Giải bài tập Cho tam giác ABC cân tại A. Kẻ BH vuông góc với AC tại H, kẻ CK vuông góc với AB tại K. Chứng minh rằng :

Đề bài

Cho tam giác ABC cân tại A. Kẻ BH vuông góc với AC tại H, kẻ CK vuông góc với AB tại K. Chứng minh rằng :

a) \(\Delta ABH = \Delta ACK.\)

b) \(\Delta AHK\) cân.

c) KH // BC.

Lời giải chi tiết

 

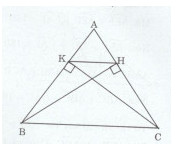
a)Xét tam giác ABH vuông tại H và tam giác ACK vuông tại K có:

\(\widehat {HAB} = \widehat {KAC}\)   (góc chung)

AB = AC (tam giác ABC cân tại A)

Do đó: \(\Delta ABH = \Delta ACK\)  (cạnh huyền - góc nhọn).

b) Ta có: \(\Delta ABH = \Delta ACK\)  (chứng minh câu a) => AH = AK => tam giác AHK cân tại A.

c)Tam giác ABC cân tại A có: \(\widehat {ABC} + \widehat {ACB} + \widehat {BAC} = {180^0}\)

\(\eqalign{  &  \Leftrightarrow \widehat {ABC} + \widehat {ABC} + \widehat {BAC} = {180^0}(vi\widehat {ABC} = \widehat {ACB})  \cr  &  \Leftrightarrow 2\widehat {ABC} + \widehat {BAC} = {180^0} \Rightarrow \widehat {ABC} = {{{{180}^0} - \widehat {BAC}} \over 2} \cr} \)

Tam giác AHK cân tại A có: \(\widehat {AKH} + \widehat {AHK} + \widehat {KAH} = {180^0}.\)

\(\eqalign{  &  \Leftrightarrow \widehat {AKH} + \widehat {AKH} + \widehat {KAH} = {180^0}(vi\widehat {AKH} = \widehat {AHK})  \cr  &  \Leftrightarrow 2\widehat {AKH} + \widehat {KAH} = {180^0} \Rightarrow \widehat {AKH} = {{{{180}^0} - \widehat {KAH}} \over 2} \cr} \)

Ta có: \(\widehat {ABC} = {{{{180}^0} - \widehat {BAC}} \over 2}\)  và \(\widehat {AKH} = {{{{180}^0} - \widehat {KAH}} \over 2} \Rightarrow \widehat {ABC} = \widehat {AKH.}\)

Mà hai góc này ở vị trí đồng vị nên HK // BC.

Loigiaihay.com


Bình chọn:
4.3 trên 12 phiếu
Bài tiếp theo

>> Xem thêm

Báo lỗi - Góp ý

Tham Gia Group Dành Cho 2K11 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí

>> Học trực tuyến lớp 8 trên Tuyensinh247.com Đầy đủ khoá học các bộ sách (Kết nối tri thức với cuộc sống; Chân trời sáng tạo; Cánh diều). Cam kết giúp học sinh lớp 8 học tốt, hoàn trả học phí nếu học không hiệu quả.

Các bài khác cùng chuyên mục


App Loigiaihay trên google play store App Loigiaihay trên apple store

Copyright © 2021 loigiaihay.com

DMCA.com Protection Status
App Loigiaihay trên apple store App Loigiaihay trên google play store

Đăng ký để nhận lời giải hay và tài liệu miễn phí

Cho phép loigiaihay.com gửi các thông báo đến bạn để nhận được các lời giải hay cũng như tài liệu miễn phí.

Đồng ý Bỏ qua