Một số bài toán dẫn đến khái niệm đạo hàm - Toán 11

Từ vị trí O (ở một độ cao nhất định nào đó), ta thả một viên bi cho rơi tự do xuống đất và nghiên cứu chuyển động của viên bi. Bằng việc chọn trục Oy theo phương thẳng đứng, chiều dương hướng xuống đất, gốc O là vị trí ban đầu của viên bi, tức là tại thời điểm 0 giây, và bỏ qua sức cản không khí, ta nhận được phương trình chuyển động của viên bi là \(y = f(x) = \frac{1}{2}g{x^2}\) (g là gia tốc rơi tự do, \(g \approx 9,8\) m/s\(^2\)).

Giả sử tại thời điểm \({x_0}\), viên bi ở vị trí \({M_0}\) có \({y_0} = f({x_0})\); tại thời điểm \({x_1}\), viên bi ở vị trí \({M_1}\) có \({y_1} = f({x_1})\).

Khi đó, trong khoảng thời gian từ \({x_0}\) đến \({x_1}\), quãng đường viên bi đi được là \({M_0}{M_1} = f({x_1}) - f({x_0})\) (hình vẽ).

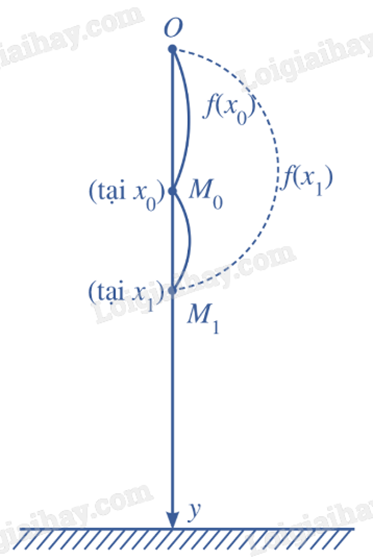
Vậy vận tốc trung bình của viên bi trong khoảng thời gian đó là \(\frac{{f({x_1}) - f({x_0})}}{{{x_1} - {x_0}}}\).

Nếu \({x_1} - {x_0}\) càng nhỏ thì tỉ số trên càng phản ánh chính xác hơn sự nhanh chậm của viên bi tại thời điểm \({x_0}\). Từ đó, người ta xem giới hạn của tỉ số \(\frac{{f({x_1}) - f({x_0})}}{{{x_1} - {x_0}}}\) khi \({x_1}\) dần đến \({x_0}\) là vận tốc tức thời tại thời điểm \({x_0}\) của viên bi, kí hiệu là \(v({x_0})\). Nói cách khác, \(v({x_0}) = \mathop {\lim }\limits_{{x_1} \to {x_0}} \frac{{f({x_1}) - f({x_0})}}{{{x_1} - {x_0}}}\).

Giá trị \(v({x_0})\) gọi là đạo hàm của hàm số \(y = f(x) = \frac{1}{2}g{x^2}\) tại điểm \({x_0}\).

Điện lượng \(Q\) truyền trong dây dẫn là một hàm số của thời gian \(t\), \(Q = Q(t)\). Cường độ trung bình trong khoảng thời gian \(|t - {t_0}|\) được xác định bởi công thức \(\frac{{Q(t) - Q({t_0})}}{{t - {t_0}}}\).

Nếu \(|t - {t_0}|\) càng nhỏ thì tỉ số này càng biểu thị chính xác hơn cường độ dòng điện tại thời điểm \({t_0}\). Người ta đưa ra định nghĩa sau đây:

Giới hạn hữu hạn (nếu có) \(\mathop {\lim }\limits_{t \to {t_0}} \frac{{Q(t) - Q({t_0})}}{{t - {t_0}}}\) được gọi là cường độ tức thời của dòng điện tại thời điểm \({t_0}\).