-
Toán 8 tập 1 - Kết nối tri thức với cuộc sống
-
Toán 8 tập 2 - Kết nối tri thức
Toán 8, giải toán lớp 8 kết nối tri thức với cuộc sống
Bài 28. Hàm số bậc nhất và đồ thị của hàm số bậc nhất T..
Lý thuyết Hàm số bậc nhất và đồ thị của hàm số bậc nhất SGK Toán 8 - Kết nối tri thức
Hàm số bậc nhất là gì?
Tổng hợp đề thi giữa kì 1 lớp 8 tất cả các môn - Kết nối tri thức
Toán - Văn - Anh - Khoa học tự nhiên
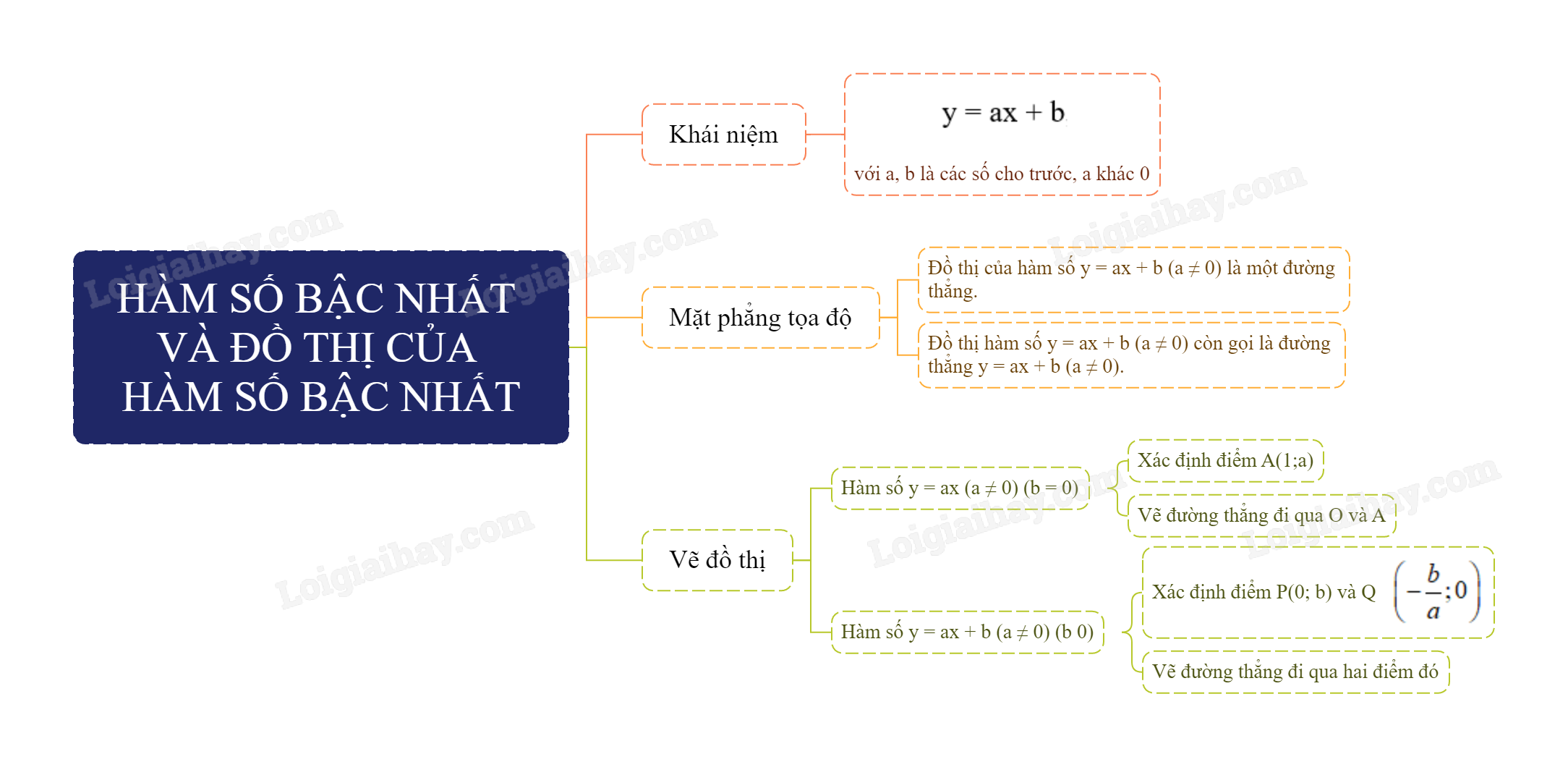
1. Hàm số bậc nhất
Khái niệm:
Hàm số bậc nhất là hàm số được cho bởi công thức y = ax + b, trong đó a, b là các số cho trước và a khác 0.
Ví dụ: y = 2x – 3 là hàm số bậc nhất với a = 2 và b = -3
y = x + 4 là hàm số bậc nhất với a = 1, b = 4
2. Mặt phẳng tọa độ
Đồ thị của hàm số y = ax + b (a\( \ne \)0) là một đường thẳng.
Chú ý: Đồ thị hàm số y = ax + b (a\( \ne \)0) còn gọi là đường thẳng y = ax + b (a\( \ne \)0).
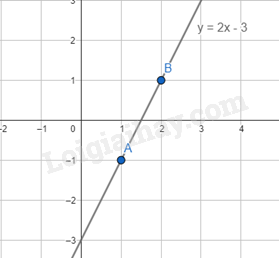
Ví dụ: Cho hàm số y = 2x – 3 có hai điểm A(1, -1) và B(2; 1) thuộc đồ thị của hàm số y = 2x – 3.
3. Vẽ đồ thị của hàm số bậc nhất
Hàm số y = ax (a\( \ne \)0) (b = 0)
Để vẽ đồ thị của hàm số y = ax (a\( \ne \)0), ta có thể xác định điểm A(1; a) rồi vẽ đường thẳng đi qua hai điểm O và A.
Hàm số y = ax + b (a\( \ne \)0) (b\( \ne \)0)
Để vẽ đồ thị của hàm số y = ax + b (a\( \ne \)0, b\( \ne \)0), ta có thể xác định hai điểm P(0; b) và Q\(\left( { - \frac{b}{a};0} \right)\) rồi vẽ dường thẳng đi qua hai điểm đó.
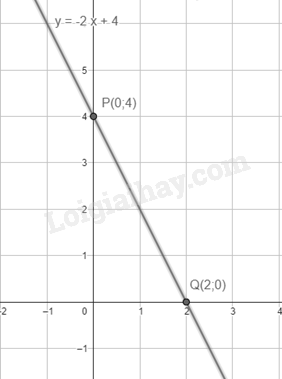
Ví dụ: Cho hàm số y = -2x + 4
Với x = 0 thì y = 4, ta được điểm P(0;4)
Với y = 0 thì x = 22, ta được điểm Q(2;0)
Vậy đồ thị hàm số y = -2x + 4 là đường thẳng đi qua hai điểm P(0;4) và Q(2;0)
Bình luận
Chia sẻ
- Giải câu hỏi mở đầu trang 47 SGK Toán 8 tập 2 - Kết nối tri thức
- Giải mục 1 trang 47, 48 SGK Toán 8 tập 2 - Kết nối tri thức
- Giải mục 2 trang 48, 49 SGK Toán 8 tập 2 - Kết nối tri thức
- Giải bài 7.24 trang 50 SGK Toán 8 tập 2 - Kết nối tri thức
- Giải bài 7.25 trang 50 SGK Toán 8 tập 2 - Kết nối tri thức
>> Xem thêm
Luyện Bài Tập Trắc nghiệm Toán 8 - Kết nối tri thức - Xem ngay
Tham Gia Group Dành Cho Lớp 8 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí
Các bài khác cùng chuyên mục
- Giải dự án 2 trang 112 SGK Toán 8 tập 1
- Lý thuyết Hình chóp tứ giác đều SGK Toán 8 - Kết nối tri thức
- Lý thuyết Hình chóp tam giác đều SGK Toán 8 - Kết nối tri thức
- Lý thuyết Hình đồng dạng SGK Toán 8 - Kết nối tri thức
- Lý thuyết Các trường hợp đồng dạng của hai tam giác vuông SGK Toán 8 - Kết nối tri thức
