Bài 3. Năng lượng trong dao động điều hòa trang 24, 25, 26, 27 Vật Lí 11 Cánh diều
Một con lắc đơn lớn được treo ở sảnh của tòa nhà Liên Hợp Quốc tại thành phố New York, Mỹ. Quả cầu có khối lượng 91 kg và sợi dây treo dài 22,9 m. Con lắc liên tục dao động với chu kì 9,6 s
Câu hỏi tr 24 KĐ
Một con lắc đơn lớn được treo ở sảnh của tòa nhà Liên Hợp Quốc tại thành phố New York, Mỹ. Quả cầu có khối lượng 91 kg và sợi dây treo dài 22,9 m. Con lắc liên tục dao động với chu kì 9,6 s.
Khi con lắc đơn dao động, nó có những dạng năng lượng nào?

Phương pháp giải:
Nhớ lại định nghĩa của động năng và thế năng: Động năng là dạng năng lượng của một vật có được do nó đang chuyển động; thế năng trọng trường của một vật là dạng năng lượng tương tác giữa Trái Đất và vật. Đối chiếu các điều kiện để có mỗi dạng năng lượng này với các đặc điểm có được trong chuyển động của quả cầu.
Lời giải chi tiết:
Khi con lắc dao động, quả cầu chuyển động nên con lắc có động năng. Quả cầu chịu tác dụng của trọng lực, ở độ cao z so với mặt đất nên con lắc có thế năng.
Câu hỏi tr 25 CH 1
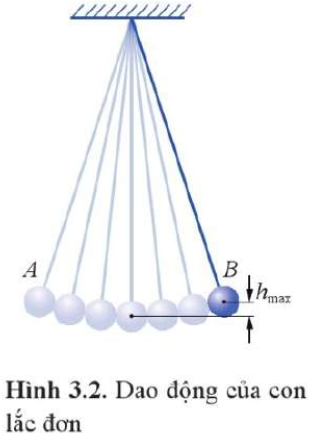
Mô tả sự biến đổi động năng và thế năng của con lắc đơn khi quả cầu đi từ vị trí biên A, qua vị trí cân bằng O rồi sang vị trí biên B
Phương pháp giải:
Sử dụng định nghĩa của thế năng và động năng: \({{\rm{W}}_t} = mgz\);\({{\rm{W}}_d} = \frac{1}{2}m{v^2}\). Từ sự thay đổi độ cao và vận tốc của quả cầu khi đi qua các vị trí suy ra sự biến đổi thế năng và động năng của con lắc đơn.
Lời giải chi tiết:
Ở vị trí biên A, quả cầu đạt độ cao cực đại nên con lắc có thế năng Wt cực đại. Khi quả cầu đi từ A đến vị trí cân bằng O, độ cao của quả cầu so với mốc thế năng giảm dần, do đó Wt giảm dần. Tại vị trí cân bằng O, độ cao của quả cầu so với mốc thế năng là cực tiểu nên thế năng của con lắc đạt cực tiểu. Từ O đến vị trí biên B, độ cao của quả cầu tăng dần, nên thế năng Wt tăng dần đến giá trị cực đại tại biên B.
Tại vị trí biên A, vận tốc của quả cầu bằng 0 nên động năng của con lắc Wđ = 0. Từ A đến O, vận tốc của quả cầu tăng dần và đạt cực đại tại vị trí cân bằng nên Wđ cũng tăng dần và đạt cực đại tại O. Sau đó, vận tốc của con lắc giảm dần và bằng 0 tại B nên động năng giảm dần từ giá trị cực đại về 0.
Câu hỏi tr 25 CH 2
Chứng minh rằng cơ năng dao động của con lắc đơn tỉ lệ thuận với bình phương của biên độ dao động
Phương pháp giải:
Cơ năng của con lắc đơn được bảo toàn. Chọn mốc thế năng tại vị trí cân bằng. Sử dụng các công thức \({{\rm{W}}_d} = \frac{1}{2}m{v^2}\), \({v_{\max }} = \omega A\).
Lời giải chi tiết:
Quả cầu chịu tác dụng của trọng lực và lực căng dây nên cơ năng của con lắc đơn được bảo toàn.
Chọn mốc thế năng tại vị trí cân bằng.
Tại vị trí cân bằng: Wt = 0, vận tốc của con lắc đạt cực đại vmax = nên động năng của con lắc đạt cực đại:
\({{\rm{W}}_{d\max }} = \frac{1}{2}m{v_{\max }}^2 = \frac{1}{2}m{\left( {\omega A} \right)^2} = \left( {\frac{1}{2}m{\omega ^2}} \right){A^2}\).
Cơ năng của con lắc là: \({\rm{W}} = {{\rm{W}}_d} + {{\rm{W}}_t} = {{\rm{W}}_{d\max }} + 0 = \left( {\frac{1}{2}m{\omega ^2}} \right){A^2}\).
Như vậy, cơ năng dao động W của con lắc đơn tỉ lệ thuận với bình phương của biên độ dao động A.
Câu hỏi tr 26 CH 1
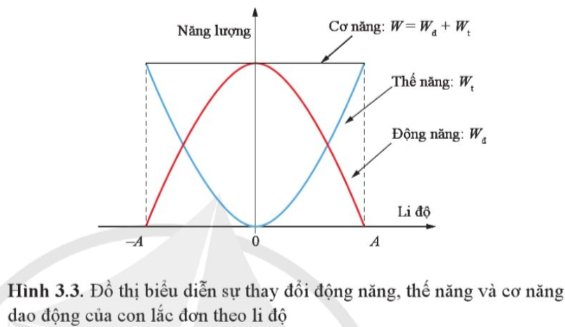
Dựa vào đồ thị Hình 3.3, mô tả sự thay đổi của động năng và thế năng của con lắc đơn khi vật đi từ vị trí biên về vị trí cân bằng và từ vị trí cân bằng đến vị trí biên
Phương pháp giải:
Quan sát đồ thị năng lượng theo li độ của con lắc đơn và mô tả sự tăng giảm, độ lớn cực đại, cực tiểu của động năng và thế năng khi đi từ biên về vị trí cân bằng và từ vị trí cân bằng đến biên
Lời giải chi tiết:
Khi vật đi từ vị trí biên về vị trí cân bằng, thế năng của con lắc đơn giảm dần từ giá trị cực đại (bằng cơ năng của con lắc) về 0 (Mốc thế năng tại vị trí cân bằng). Do cơ năng của con lắc được bảo toàn, tổng của động năng và thế năng không đổi nên thế năng giảm bao nhiêu, động năng tăng bấy nhiêu. Do đó, khi vật đi từ biên về vị trí cân bằng, động năng của vật tăng từ 0 đến cực đại.
Khi vật đi từ vị trí cân bằng về vị trí biên, thế năng của con lắc tăng dần từ 0 đến cực đại, trong khi động năng giảm dần từ cực đại về 0.
Câu hỏi tr 26 CH 2
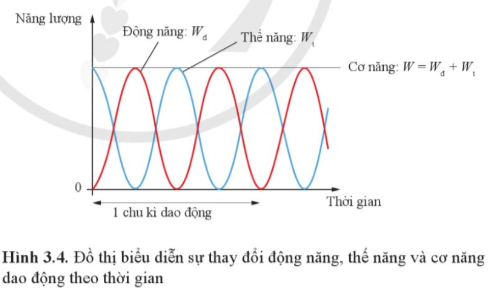
Dựa vào đồ thị Hình 3.4, tìm số lần vật có động năng bằng thế năng trong mỗi chu kì dao động của vật
Phương pháp giải:
Quan sát đồ thị, tìm số điểm giao nhau của hai đường biểu diễn động năng và thế năng theo thời gian trong một chu kì.
Lời giải chi tiết:
Xét trong một chu kì, đồ thị của động năng và thế năng cắt nhau tại 4 điểm, nghĩa là có 4 lần vật có động năng bằng thế năng trong mỗi chu kì dao động của vật.
Câu hỏi tr 26 CH 3
So sánh chu kì biến đổi của động năng và thế năng với chu kì dao động của vật
Phương pháp giải:
Chu kì biến đổi của động năng và thế năng là bằng nhau. Biến đổi công thức tính động năng hoặc thế năng, sử dụng phương trình li độ
Lời giải chi tiết:
Chu kì biến đổi của động năng và thế năng là bằng nhau.
\({{\rm{W}}_d} = \frac{1}{2}m{v^2} = \frac{1}{2}m{\left( { - \omega A\sin \left( {\omega t + \varphi } \right)} \right)^2} = \left( {\frac{1}{2}m{\omega ^2}{A^2}} \right)\left( {\frac{{1 - \cos \left( {2\omega t + 2\varphi } \right)}}{2}} \right)\).
Như vậy, động năng và thế năng biến đổi với chu kì \(T = \frac{{2\pi }}{{2\omega }}\), bằng một nửa chu kì dao động.
Câu hỏi tr 27 CH 1
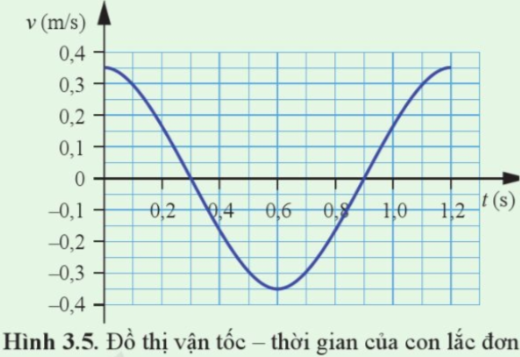
Cho đồ thị vận tốc – thời gian của một con lắc đơn dao động như Hình 3.5. Biết rằng khối lượng của vật treo vào sợi dây là 0,2 kg. Xác định:
a. Chu kì và tần số góc của con lắc.
b. Vận tốc cực đại của con lắc.
c. Cơ năng của con lắc.
d. Biên độ của vật
Phương pháp giải:
Quan sát đồ thị, chỉ ra chu kì dao động T của con lắc. Từ đó, sử dụng các công thức tính các đại lượng mà đề yêu cầu qua các đại lượng đã biết
Lời giải chi tiết:
a. Dựa vào đồ thị, ta có: Chu kì dao động là T = 1,2 s.
Tần số góc của con lắc là: \(\omega = \frac{{2\pi }}{T} = \frac{{2\pi }}{{1,2}} = \frac{{5\pi }}{3}\)(rad/s).
b. Dựa vào đồ thị, ta thấy: Vận tốc cực đại của con lắc là: \({v_{\max }} = 0,35\)m/s.
c. Cơ năng của con lắc được bảo toàn và bằng động năng cực đại. Cơ năng của con lắc là:
\({\rm{W}} = {{\rm{W}}_{d\max }} = \frac{1}{2}m{v_{\max }}^2 = \frac{1}{2}.0,2.0,{35^2} = 0,01225\)(J).
d. Biên độ dao động của con lắc là: \(A = \frac{{{v_{\max }}}}{\omega } = \frac{{0,35}}{{\frac{{5\pi }}{3}}} \approx 0,0668\) (m).
Câu hỏi tr 27 CH 2
Khi nghiên cứu sự biến đổi năng lượng của con lắc đơn trong quá trình dao động, có bạn học sinh khẳng định rằng, nếu ta thay một quả lắc khác có khối lượng lớn hơn nhưng vẫn giữ nguyên biên độ của dao động thì vận tốc của quả lắc mới sẽ lớn hơn khi qua vị trí cân bằng vì nó có cơ năng lớn hơn.
Nhận thức này đúng hay sai? Vì sao?
Phương pháp giải:
Viết biểu thức tính cơ năng (bằng thế năng cực đại) và biểu thức tính động năng tại vị trí cân bằng để giải thích.
Lời giải chi tiết:
Nhận định của bạn học sinh là sai.
Giải thích: Trong quá trình dao động, cơ năng của con lắc được bảo toàn và có giá trị bằng thế năng cực đại và động năng cực đại.
\({\rm{W}} = {{\rm{W}}_{t\max }}{\rm{ = mg}}{{\rm{h}}_{\max }}\); \({\rm{W = }}{{\rm{W}}_{d\max }} = \frac{1}{2}m{v_{\max }}^2\). Suy ra, \({v_{\max }}^2 = 2g{{\rm{h}}_{\max }}\). Từ đó ta thấy, biên độ dao động không đổi thì \({{\rm{h}}_{\max }}\) không đổi, do đó vận tốc tại vị trí cân bằng (vận tốc cực đại) cũng không đổi, hay khối lượng của vật không ảnh hưởng đến vận tốc của vật tại vị trí cân bằng.
Câu hỏi tr 27 CH 3
Đồ thị Hình 3.6 mô tả sự thay đổi động năng theo li dộ của quả cầu có khối lượng 0,4 kg trong một con lắc lò xo treo thẳng đứng. Xác định:
a) Cơ năng của con lắc lò xo.
b) Vận tốc cực đại của quả cầu.
c) Thế năng của con lắc lò xo khi quả cầu ở vị trí có li độ 2 cm.
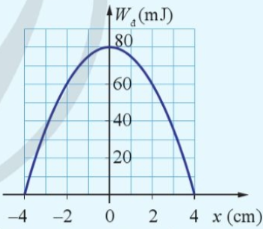
Lời giải chi tiết:
a) Cơ năng của con lắc lò xo được bảo toàn và bằng:
\({\rm{W}} = {{\rm{W}}_d} + {{\rm{W}}_t} = {{\rm{W}}_{d\max }} = 80\) (mJ) = 0,08 J.
b) Vận tốc cực đại của quả cầu là vmax. Động năng cực đại của con lắc lò xo là:
\({{\rm{W}}_{d\max }} = \frac{1}{2}m{v_{\max }}^2\)
Do đó, vận tốc cực đại của con lắc là:
\({v_{\max }} = \sqrt {\frac{{2{{\rm{W}}_{d\max }}}}{m}} = \sqrt {\frac{{2.0,08}}{{0,4}}} = \frac{{\sqrt {10} }}{5}\) (m/s).
c) Khi quả cầu có li độ 2 cm, động năng của con lắc là Wđ = 60 mJ.
Tại đó, thế năng của con lắc là: \({{\rm{W}}_t} = {\rm{W}} - {{\rm{W}}_d} = 80 - 60 = 20\)(mJ).
Các bài khác cùng chuyên mục













Danh sách bình luận