Giải mục 3 trang 75, 76, 77, 78, 79 Chuyên đề học tập Toán 11 - Chân trời sáng tạo

Khám phá 4

Cho hình hộp chữ nhật \(OABC.{O_1}{A_1}{B_1}{C_1}.\) Ba tia Ox, Oy, Oz lần lượt chứa ba cạnh OA, OC, OO₁. Cho mặt phẳng (P) và đường thẳng l không song song với (P). Tìm ảnh của hình hộp chữ nhật OABC.O₁A₁B₁C₁ và ảnh của các tia Ox, Oy, Oz qua phép chiếu song song theo phương l lên mặt phẳng (P).

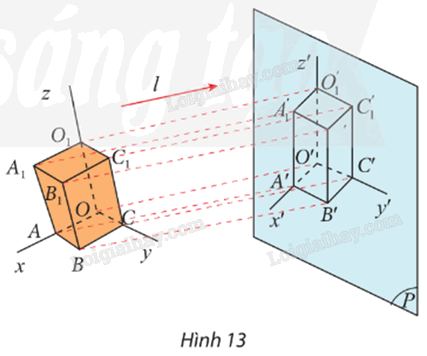
Phương pháp giải:

Để tìm ảnh của hình ta tìm ảnh của từng điểm qua phép chiếu song song theo phương l lên mặt phẳng (P).

Lời giải chi tiết:

– Ta có OO’ // l và \(O' \in \left( P \right).\)

Suy ra O’ là ảnh của O qua phép chiếu song song theo phương l lên mặt phẳng (P).

Chứng minh tương tự, ta được A’, B’, C’, lần lượt là ảnh của A, B, C, O₁, A₁, B₁, C₁ qua phép chiếu song song theo phương l lên mặt phẳng (P).

Do đó là ảnh của hình hộp chữ nhật OABC.O₁A₁B₁C₁ qua phép chiếu song song theo phương l lên mặt phẳng (P).

– Ta có O’, A’ lần lượt là ảnh của O, A qua phép chiếu song song theo phương l lên mặt phẳng (P).

Suy ra O’A’ là ảnh của OA qua phép chiếu song song theo phương l lên mặt phẳng (P).

Mà A’ ∈ O’x’.

Do đó O’x’ là ảnh của Ox qua phép chiếu song song theo phương l lên mặt phẳng (P).

Chứng minh tương tự, ta được O’y’, O’z’ lần lượt là ảnh của Oy, Oz qua phép chiếu song song theo phương l lên mặt phẳng (P).

Vậy ảnh của hình hộp chữ nhật OABC.O₁A₁B₁C₁ và ảnh của các tia Ox, Oy, Oz qua phép chiếu song song theo phương l lên mặt phẳng (P) lần lượt là hình hộp chữ nhật và các tia O’x’, O’y’, O’z’.

Khám phá 5

Cho hình lập phương ABCD.A’B’C’D’ có cạnh bằng đơn vị (Hình 14).

a) Chỉ ra rằng \(AC' \bot \left( {A'BD} \right).\)

b) Gọi O là tâm của tam giác đều A’BD. Hình chiếu vuông góc của ba đoạn AB, AD và AA’ lên (A’BD) có bằng nhau không?

c) Chỉ ra rằng \(\widehat {BOD} = \widehat {DOA'} = \widehat {A'OB} = 120^\circ \)

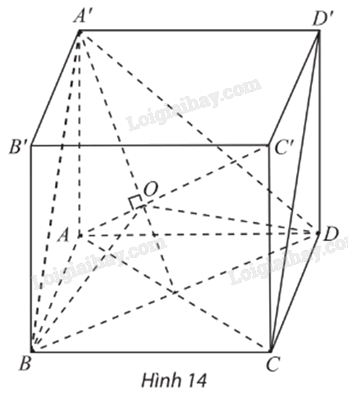
Phương pháp giải:

Để chứng minh đường thẳng \(d \bot (P)\) ta chứng minh d vuông góc với 2 đường thẳng cắt nhau nằm trong (P).

Lời giải chi tiết:

a) Ta có \(A'D \bot AD'\) (AA’D’D là hình vuông) và \(A'D \bot C'D'{\rm{ }}(C'D' \bot \left( {AA'D'D} \right)).\)
Suy ra \(A'D \bot \left( {AC'D'} \right).\)

Do đó \(A'D \bot AC'{\rm{ }}\left( 1 \right)\)

Chứng minh tương tự, ta được \(A'B \bot AC'{\rm{ }}\left( 2 \right)\)

Từ (1), (2), ta thu được \(AC' \bot \left( {A'BD} \right).\)

b) Gọi M là trung điểm BD.

Ta có AB = AD (do ABCD là hình vuông).

Suy ra tam giác ABD cân tại A.

Do đó AM ⊥ BD.

Lại có O là tâm của tam giác đều A’BD.

Suy ra \(A'M \bot BD\)  và \(O \in A'M\).

Ta có \(AM \bot BD\)  và \(A'M \bot BD\) (chứng minh trên).

Suy ra \(BD \bot \left( {AA'M} \right).\)

Do đó \(BD \bot AO{\rm{ }}\left( 3 \right)\)

Chứng minh tương tự, ta được \(A'D \bot AO{\rm{ }}\left( 4 \right)\)

Từ (3), (4), suy ra \(AO \bot \left( {A'BD} \right).\)

Khi đó O là hình chiếu vuông góc của A lên mặt phẳng (A’BD).

Mà B là hình chiếu vuông góc của B lên mặt phẳng (A’BD).

Suy ra OB là hình chiếu vuông góc của AB lên mặt phẳng (A’BD).

Chứng minh tương tự, ta được: OD, OA’ lần lượt là hình chiếu vuông góc của AD, AA’ lên mặt phẳng (A’BD).

Tam giác A’BD đều có tâm O.

Suy ra OA’ = OB = OD.

Vậy hình chiếu vuông góc OB, OD và OA’ lần lượt của ba đoạn AB, AD và AA’ lên (A’BD) có độ dài bằng nhau.

c) Ta có tam giác A’BD đều. Suy ra \(\widehat {BA'D} = 60^\circ \)

Tam giác A’BD đều có tâm O. Suy ra O là tâm đường tròn ngoại tiếp tam giác A’BD.

Khi đó \(\widehat {BOD} = 2\widehat {BA'D} = 2.60^\circ  = 120^\circ \)

Chứng minh tương tự, ta được \(\widehat {DOA'} = 120^\circ \)  và \(\widehat {A'OB} = 120^\circ \)

Vậy \(\widehat {BOD} = \widehat {DOA'} = \widehat {A'OB} = 120^\circ \)

Thực hành 3

Vẽ trên giấy kẻ ô li hình biểu diễn của hình lăng trụ đứng có đáy là tam giác vuông với các kích thước được cho như trong Hình 23 (quy tắc mỗi cạnh của tam giác đều biểu diễn độ dài 1 cm).

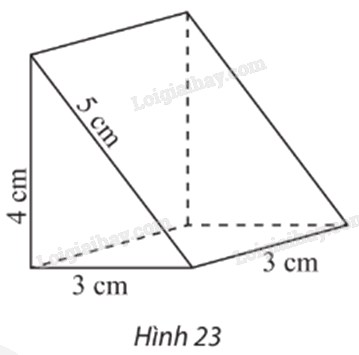
Phương pháp giải:

Hình biểu diễn của một hình khối H trong không gian là hình chiếu song song hoặc vuông góc của H lên mặt phẳng.

Lời giải chi tiết:

Hình biểu diễn của hình lăng trụ đứng có đáy là tam giác vuông với các kích thước được cho như trong Hình 23 là:

Vận dụng 3

Tìm các kích thước a, b, c, d, e của chi tiết cơ khí trong Hình 24a có hình biểu diễn được vẽ trên giấy kẻ ô li là Hình 24b với quy ước mỗi cạnh của tam giác đều biểu diễn độ dài 1 cm.

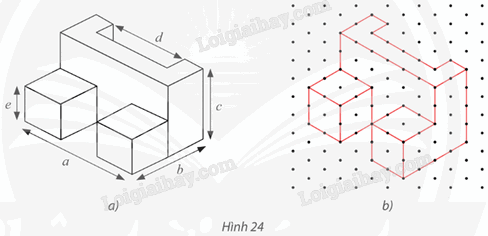
Phương pháp giải:

Quan sát hình 24 để trả lời

Lời giải chi tiết:

Các kích thước a, b, c, d, e của chi tiết cơ khí trong Hình 24a được biểu diễn trên Hình 24b như sau:

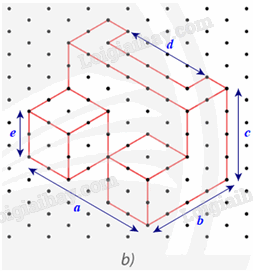
Do mỗi cạnh của tam giác đều biểu diễn độ dài 1 cm nên ta có:

Chiều dài a = 6 cm; chiều rộng b = 4 cm; chiều cao c = 4 cm; bề dày d = 4 cm; bề dày e = 2 cm.