Giải mục 3 trang 25 SGK Toán 8 tập 1– Chân trời sáng tạo

Hãy hoàn thành biến đổi sau vào vở để phân tích đa thức thành nhân tử: ({a^2} + ab + 2a + 2b = left( {{a^2} + ab} right) + left( {2a + 2b} right) = ...) Em có thể biến đổi theo cách khác để phân tích đa thức trên thành nhân tử không?

Lựa chọn câu để xem lời giải nhanh hơn

HĐ3

Video hướng dẫn giải

Hãy hoàn thành biến đổi sau vào vở để phân tích đa thức thành nhân tử:

\({a^2} + ab + 2a + 2b = \left( {{a^2} + ab} \right) + \left( {2a + 2b} \right) = ...\)

Em có thể biến đổi theo cách khác để phân tích đa thức trên thành nhân tử không?

Phương pháp giải:

Sử dụng phương pháp đặt nhân tử chung để phân tích đa thức thành nhân tử.

Lời giải chi tiết:

\({a^2} + ab + 2a + 2b \\= \left( {{a^2} + ab} \right) + \left( {2a + 2b} \right) \\= a\left( {a + b} \right) + 2\left( {a + b} \right) \\= \left( {a + b} \right)\left( {a + 2} \right)\)

Cách khác:

\({a^2} + ab + 2a + 2b \\= \left( {{a^2} + 2a} \right) + \left( {ab + 2b} \right) \\= a\left( {a + 2} \right) + b\left( {a + 2} \right) \\= \left( {a + 2} \right)\left( {a + b} \right)\)

TH3

Video hướng dẫn giải

Phân tích các đa thức sau thành nhân tử:

a) \({a^3} - {a^2}b + a - b\)

b) \({x^2} - {y^2} + 2y - 1\)

Phương pháp giải:

a) Sử dụng phương pháp nhóm hạng tử

b) Sử dụng phương pháp nhóm hạng tử, hẳng đẳng thức \({\left( {a - b} \right)^2} = {a^2} - 2ab + {b^2}\), \({a^2} - {b^2} = \left( {a + b} \right)\left( {a - b} \right)\)

Lời giải chi tiết:

a) \({a^3} - {a^2}b + a - b\)

\( = \left( {{a^3} - {a^2}b} \right) + \left( {a - b} \right) \\= {a^2}\left( {a - b} \right) + \left( {a - b} \right) \\= \left( {a - b} \right)\left( {{a^2} + 1} \right)\)

b) \({x^2} - {y^2} + 2y - 1\)

\( = {x^2} - {\left( {{y^2} - 2y + 1} \right)^2} = {x^2} - {\left( {y - 1} \right)^2} \\= \left[ {x + \left( {y - 1} \right)} \right]\left[ {x - \left( {y - 1} \right)} \right] \\= \left( {x + y - 1} \right)\left( {x - y + 1} \right)\)

VD3

Video hướng dẫn giải

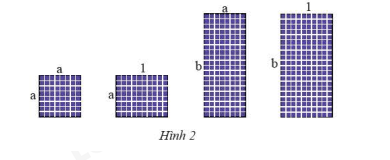
Có thể ghép bốn tấm pin mặt trời với kích thước như Hình 2 thành một hình chữ nhật không? Nếu có, tính độ dài các cạnh và diện tích hình chữ nhật đó. Biết \(a = 0,8\); \(b = 2\) (các kích thước tính theo mét).