 Toán 8, giải toán lớp 8 chân trời sáng tạo
Toán 8, giải toán lớp 8 chân trời sáng tạo
 Bài 1. Định lí Thalès trong tam giác Toán 8 chân trời s..
Bài 1. Định lí Thalès trong tam giác Toán 8 chân trời s..
Giải mục 1 trang 44, 45 SGK Toán 8 tập 2– Chân trời sáng tạo
a) Cho hai số 5 và 8. Hãy tính tỉ số giữa hai số đã cho.
HĐ1
Video hướng dẫn giải
a) Cho hai số 5 và 8. Hãy tính tỉ số giữa hai số đã cho.
b) Hãy đo và tính tỉ số giữa hai độ dài (theo mm) của hai đoạn thẳng \(AB\) và \(CD\) trong Hình 1.

Phương pháp giải:
Tỉ số giữa hai đoạn thẳng là tỉ số độ dài của hai đoạn thẳng khi cùng đơn vị đo.
Lời giải chi tiết:
a) Tỉ số giữa hai số 5 và 8 là \(5:8 = \frac{5}{8}\).
b) Ta có: AB = 35mm; CD = 45mm
Tỉ số giữa hai đoạn thẳng \(AB\) và \(CD\) là \(AB:CD = \frac{{AB}}{{CD}} = \frac{35}{45}=\frac{7}{9}\).
TH1
Video hướng dẫn giải
Hãy tính tỉ số của hai đoạn thẳng \(AB\) và \(CD\) trong các trường hợp sau:
a) \(AB = 6cm;CD = 8cm\);
b) \(AB = 1,2m;CD = 42cm\).
Phương pháp giải:
Tỉ số giữa hai đoạn thẳng là tỉ số độ dài của hai đoạn thẳng khi cùng đơn vị đo.
Lời giải chi tiết:
a) Tỉ số giữa hai đoạn thẳng \(AB\) và \(CD\) là \(AB:CD = \frac{{AB}}{{CD}} = \frac{6}{8} = \frac{3}{4}\).
b) Đổi \(1,2m = 120cm\)
Tỉ số giữa hai đoạn thẳng \(AB\) và \(CD\) là \(AB:CD = \frac{{AB}}{{CD}} = \frac{{120}}{{42}} = \frac{{20}}{7}\).
HĐ2
Video hướng dẫn giải
So sánh tỉ số của hai đoạn thẳng \(AB\) và \(CD\) với tỉ số của hai đoạn thẳng \(EF\) và \(MN\) trong Hình 2.
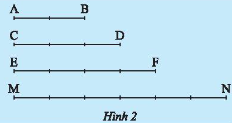
Phương pháp giải:
Ta tính tỉ số của hai đoạn thẳng \(AB\) và \(CD\) ; tỉ số của hai đoạn thẳng \(EF\) và \(MN\) sau đó so sánh.
Lời giải chi tiết:
Ta coi mỗi vạch chia là 1 đơn vị. Do đó, độ dài các đoạn thẳng là \(AB = 2\) đơn vị; \(CD = 3\) đơn vị; \(EF = 4\) đơn vị; \(MN = 6\) đơn vị.
Tỉ số giữa hai đoạn thẳng \(AB\) và \(CD\) là \(AB:CD = \frac{{AB}}{{CD}} = \frac{2}{3}\).
Tỉ số giữa hai đoạn thẳng \(EF\) và \(MN\) là \(EF:MN = \frac{{EF}}{{MN}} = \frac{4}{6} = \frac{2}{3}\).
Do đó, tỉ số của hai đoạn thẳng \(AB\) và \(CD\) bằng tỉ số của hai đoạn thẳng \(EF\) và \(MN\) .
TH2
Video hướng dẫn giải
Trong Hình 3, chứng minh rằng:
a) \(AB\) và \(BC\) tỉ lệ với \(A'B'\) và \(B'C'\);
b) \(AC\) và \(A'C'\) tỉ lệ với \(AB\) và \(A'B'\).

Phương pháp giải:
Tỉ số giữa hai đoạn thẳng là tỉ số độ dài của hai đoạn thẳng khi cùng đơn vị đo.
Lời giải chi tiết:
Ta xem độ dài một cạnh của hình vuông nhỏ là \(a\) và đường chéo của một hình vuông nhỏ là \(b\).
Khi đó, độ dài các đoạn thẳng là
\(AB = b;BC = 3b;A'B' = a;B'C' = 3a;AC = 4b;A'C' = 4a\)
a) Tỉ số của \(AB\) và \(BC\)là \(\frac{{AB}}{{BC}} = \frac{b}{{3b}} = \frac{1}{3}\).
Tỉ số của \(A'B'\) và \(B'C'\) là \(\frac{{A'B'}}{{B'C'}} = \frac{a}{{3a}} = \frac{1}{3}\).
Do đó, \(AB\) và \(BC\) tỉ lệ với \(A'B'\) và \(B'C'\).
b) Tỉ số của \(AC\) và \(A'C'\)là \(\frac{{AC}}{{A'C'}} = \frac{{4b}}{{4a}} = \frac{b}{a}\).
Tỉ số của \(AB\) và \(A'B'\) là \(\frac{{AB}}{{A'B'}} = \frac{b}{a}\).
Do đó, \(AC\) và \(A'C'\) tỉ lệ với \(AB\) và \(A'B'\).
VD1
Video hướng dẫn giải
Hãy tìm các đoạn thẳng tỉ lệ trong hình vẽ sơ đồ một góc công viên ở Hình 4.

Phương pháp giải:
Tỉ số giữa hai đoạn thẳng là tỉ số độ dài của hai đoạn thẳng khi cùng đơn vị đo.
Lời giải chi tiết:
Ta có:
\(AD = 1,5m;AE = 3m;BD = 3m;EC = 6m;\)
\(AB = AD + DB = 1,5 + 3 = 4,5m;AC = AE + EC = 3 + 6 = 9m\)
Ta có:
\(\frac{{AD}}{{BD}} = \frac{{1,5}}{3} = \frac{1}{2};\frac{{AE}}{{EC}} = \frac{3}{6} = \frac{1}{2}\). Do đó, \(AD\) và \(BD\) tỉ lệ với \(AE\) và \(EC\).
\(\frac{{AD}}{{AB}} = \frac{{1,5}}{{4,5}} = \frac{1}{3};\frac{{AE}}{{AC}} = \frac{3}{9} = \frac{1}{3}\). Do đó, \(AD\) và \(AB\) tỉ lệ với \(AE\) và \(AC\).
\(\frac{{AB}}{{BD}} = \frac{{4,5}}{3} = \frac{3}{2};\frac{{AC}}{{EC}} = \frac{9}{6} = \frac{3}{2}\). Do đó, \(AB\) và \(BD\) tỉ lệ với \(AC\) và \(EC\).
- Giải mục 2 trang 46, 47, 48, 49 SGK Toán 8 tập 2– Chân trời sáng tạo
- Giải bài 1 trang 49 SGK Toán 8 tập 2– Chân trời sáng tạo
- Giải bài 2 trang 49 SGK Toán 8 tập 2– Chân trời sáng tạo
- Giải bài 3 trang 50 SGK Toán 8 tập 2– Chân trời sáng tạo
- Giải bài 4 trang 50 SGK Toán 8 tập 2– Chân trời sáng tạo
>> Xem thêm
Luyện Bài Tập Trắc nghiệm Toán 8 - Chân trời sáng tạo - Xem ngay
Các bài khác cùng chuyên mục
- Lý thuyết Xác suất lí thuyết và xác suất thực nghiệm SGK Toán 8 - Chân trời sáng tạo
- Lý thuyết Mô tả xác suất bằng tỉ số SGK Toán 8 - Chân trời sáng tạo
- Lý thuyết Hai hình đồng dạng SGK Toán 8 - Chân trời sáng tạo
- Lý thuyết Các trường hợp đồng dạng của hai tam giác vuông SGK Toán 8 - Chân trời sáng tạo
- Lý thuyết Các trường hợp đồng dạng của hai tam giác SGK Toán 8 - Chân trời sáng tạo
- Lý thuyết Xác suất lí thuyết và xác suất thực nghiệm SGK Toán 8 - Chân trời sáng tạo
- Lý thuyết Mô tả xác suất bằng tỉ số SGK Toán 8 - Chân trời sáng tạo
- Lý thuyết Hai hình đồng dạng SGK Toán 8 - Chân trời sáng tạo
- Lý thuyết Các trường hợp đồng dạng của hai tam giác vuông SGK Toán 8 - Chân trời sáng tạo
- Lý thuyết Các trường hợp đồng dạng của hai tam giác SGK Toán 8 - Chân trời sáng tạo












Danh sách bình luận