Cùng em học toán lớp 4 Cùng em học toán lớp 4 tập 2

Tuần 20: Phân số. Phân số và phép chia số tự nhiên. Phân số bằng nhau (trang 8)


Viết (theo mẫu) : Tô màu để được hình tương ứng với phân số (theo mẫu):

Lựa chọn câu để xem lời giải nhanh hơn

Bài 1

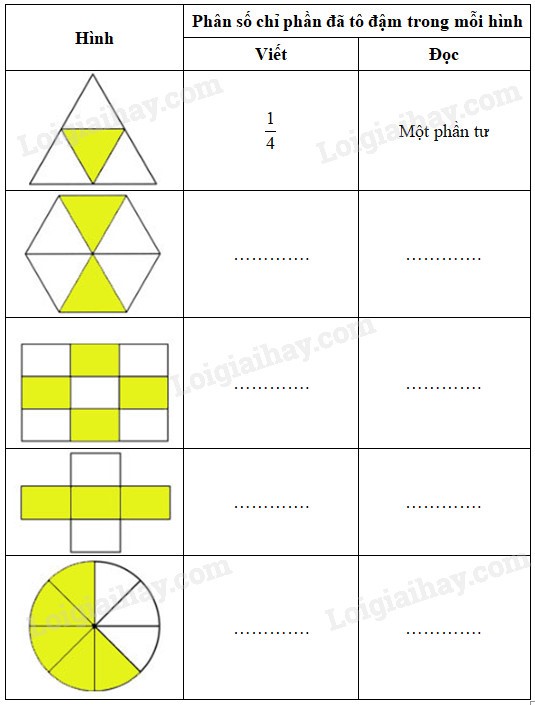
Viết (theo mẫu):

Phương pháp giải:

- Mỗi phân số có tử số và mẫu số. Tử số là số tự nhiên viết trên gạch ngang. Mẫu số là số tự nhiên khác \(0\) viết dưới gạch ngang.

- Khi đọc phân số ta đọc tử số trước, dấu gạch ngang đọc là “phần”, sau đó đọc mẫu số.

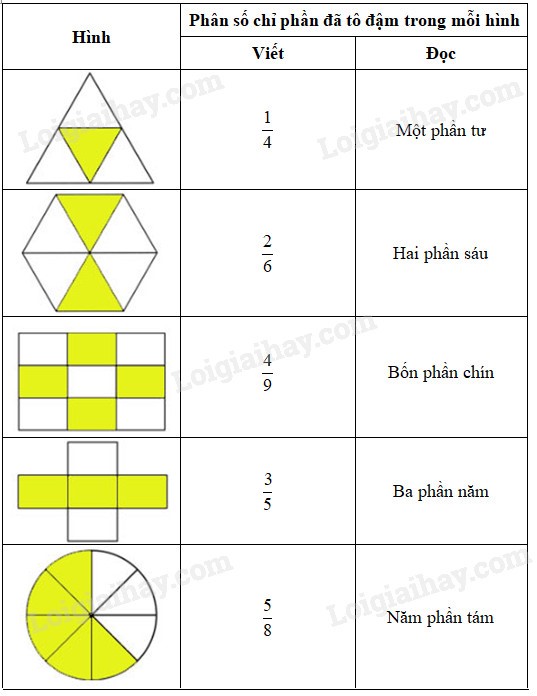
Lời giải chi tiết:

Bài 2

Viết (theo mẫu):

Phân số

Tử số

Mẫu số

\(\dfrac{7}{3}\)

7

3

\(\dfrac{4}{5}\)

 

 

\(\dfrac{9}{{17}}\)

 

 

 

Phân số

Tử số

Mẫu số

 

2

7

\(\dfrac{{13}}{{15}}\)

 

 

 

21

27

Phương pháp giải:

Mỗi phân số có tử số và mẫu số. Tử số là số tự nhiên viết trên gạch ngang. Mẫu số là số tự nhiên khác \(0\) viết dưới gạch ngang.

Lời giải chi tiết:

Phân số

Tử số

Mẫu số

\(\dfrac{7}{3}\)

7

3

\(\dfrac{4}{5}\)

4

5

\(\dfrac{9}{{17}}\)

9

17

 

Phân số

Tử số

Mẫu số

\(\dfrac{2}{7}\)

2

7

\(\dfrac{{13}}{{15}}\)

13

15

\(\dfrac{{21}}{{27}}\)

21

27

Bài 3

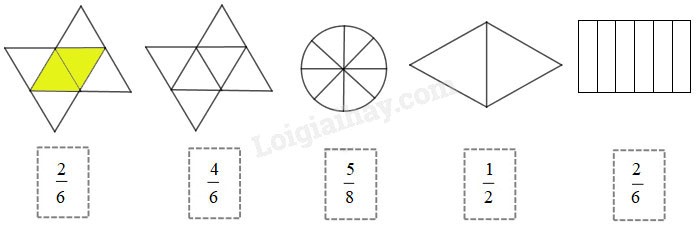
Tô màu để được hình tương ứng với phân số (theo mẫu):

Phương pháp giải:

Dựa vào phân số đã cho để tô màu vào các ô. Phân số chỉ phần được tô màu có tử số là số phần được tô màu và mẫu số là tổng số phần bằng nhau. 

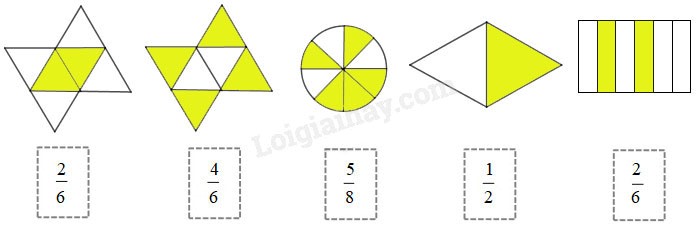
Lời giải chi tiết:

Bài 4

Viết (theo mẫu):

a) Mẫu: \(1:4 = \dfrac{1}{4}\)

    \(5:17 =  \ldots \)                       \(4:25 =  \ldots \)

b) Mẫu: \(12:3 = \dfrac{{12}}{3}\)

    \(24:8=  \ldots \)                       \(36:6 =  \ldots \)

Phương pháp giải:

Thương của phép chia số tự nhiên cho số tự nhiên (khác \(0\)) có thể viết thành một phân số, tử số là số bị chia và mẫu số là số chia.

Lời giải chi tiết:

a) \(5:17 = \dfrac{5}{{17}}\) ;                 \(4:25 = \dfrac{4}{{25}}\)

b) \(24:8 = \dfrac{{24}}{8}\)  ;                \(36:6 = \dfrac{{36}}{6}\)

Bài 5

Viết mỗi số tự nhiên dưới dạng một phân số có mẫu số bằng \(1\) (theo mẫu):

Mẫu: \(5 = \dfrac{5}{1};\)                       \(9 =  \ldots \) 

  \(3 =  \ldots \)                              \(11 =  \ldots \)

Phương pháp giải:

Mọi số tự nhiên có thể viết thành phân số có tử số là số tự nhiên đó và mẫu số bằng \(1\) .

Lời giải chi tiết:

\(9 = \dfrac{9}{1}\) ;           \(3 = \dfrac{3}{1}\) ;             \(11 = \dfrac{{11}}{1}\)

Bài 6

a) Tô màu vào ô chứa phân số bé hơn 1:

b) Tô màu vào ô chứa phân số bằng 1:

Phương pháp giải:

- Phân số có tử số lớn hơn mẫu số thì phân số đó lớn hơn \(1\).

- Phân số có tử số bằng mẫu số thì phân số đó bằng \(1\).

Lời giải chi tiết:

a) 

b) 

 

Bài 7

Viết số thích hợp vào ô trống để được hai phân số bằng nhau: 

Phương pháp giải:

Áp dụng tính chất cơ bản của phân số như sau:

- Nếu nhân cả tử số và mẫu số của một phân số với cùng một số tự nhiên khác \(0\) thì được một phân số bằng phân số đã cho.

- Nếu cả tử số và mẫu số của một phân số cùng chia hết cho một số tự nhiên khác \(0\) thì sau khi chia ta được một phân số bằng phân số đã cho.

Lời giải chi tiết:

\(\dfrac{2}{3} = \dfrac{{2 \times 4}}{{3 \times 4}} = \dfrac{8}{{12}}\;;\)                    \(\dfrac{{10}}{{30}} = \dfrac{{10\times 3}}{{30\times 3}} = \dfrac{30}{90}\;;\)                     \(\dfrac{25}{{50}} = \dfrac{{25:25}}{{50:25}} = \dfrac{1}{2}\;;\)

\(\dfrac{{21}}{{49}} = \dfrac{{21:7}}{{49:7}} = \dfrac{3}{7}\;;\)                    \(\dfrac{2}{9} = \dfrac{{2 \times 8}}{{9 \times 8}} = \dfrac{{16}}{{72}}\;;\)                    \(\dfrac{{30}}{{18}} = \dfrac{{30:6}}{{18:6}} = \dfrac{5}{3}.\)

Vậy:

\(\dfrac{2}{3} = \dfrac{8}{{12}}\;;\)                      \(\dfrac{{10}}{{30}} = \dfrac{30}{90}\;;\)

\(\dfrac{25}{{50}} = \dfrac{1}{2}\;;\)                       \(\dfrac{3}{7} = \dfrac{{21}}{{49}}\;;\)

\(\dfrac{2}{9} = \dfrac{{16}}{{72}}\;;\)                       \(\dfrac{5}{3} = \dfrac{{30}}{{18}}.\)

Bài 8

Viết phân số thích hợp vào chỗ chấm:

a) Có 4 quả táo chia đều cho 5 người, mỗi người nhận được ……. quả táo.

b) Có 3 lít nước, rót đều vào 6 lọ, mỗi lọ có ……. lít nước.

Phương pháp giải:

Thương của phép chia số tự nhiên cho số tự nhiên (khác \(0\)) có thể viết thành một phân số, tử số là số bị chia và mẫu số là số chia.

Lời giải chi tiết:

a) Có 4 quả táo chia đều cho 5 người, mỗi người nhận được \(\dfrac{4}{5}\) quả táo.

b) Có 3 lít nước, rót đều vào 6 lọ, mỗi lọ có \(\dfrac{3}{6}\) lít nước.

Vui học

Viết phân số thích hợp vào chỗ chấm:

Trên sân trường, người ta trồng 4 cây bằng lăng, 5 cây phượng vĩ, 6 cây bàng.

Phân số chỉ phần cây bằng lăng trong các cây trên sân trường là …….

Phân số chỉ phần cây bàng trong các cây trên sân trường là …….

Phân số chỉ phần cây phượng vĩ trong các cây trên sân trường là ……. 

Phương pháp giải:

Tính tổng số cây hoa trong vườn nhà Lan, sau đó viết phân số chỉ từng loại cây trong vườn.

Lời giải chi tiết:

Trên sân trường người ta trồng tổng số cây là:

            4 + 5 + 6 = 15 (cây)

Phân số chỉ phần cây bằng lăng trong các cây trên sân trường là \(\dfrac{4}{{15}}\).

Phân số chỉ phần cây bàng trong các cây trên sân trường là \(\dfrac{5}{{15}}\).

Phân số chỉ phần cây phượng vĩ trong các cây trên sân trường là \(\dfrac{6}{{15}}\).

Loigiaihay.com


Bình chọn:
4.4 trên 29 phiếu
Bài tiếp theo

>> Xem thêm

Luyện Bài Tập Trắc nghiệm Toán lớp 4 - Xem ngay

Báo lỗi - Góp ý

Tham Gia Group Dành Cho 2K15 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí

Các bài khác cùng chuyên mục


App Loigiaihay trên google play store App Loigiaihay trên apple store

Copyright © 2021 loigiaihay.com

DMCA.com Protection Status
App Loigiaihay trên apple store App Loigiaihay trên google play store