Giải Bài 97 trang 97 sách bài tập toán 7 - Cánh diều

Cho tam giác ABC vuông tại A có AB < AC, đường phân giác BD. Vẽ DE vuông góc với BC tại E.

Đề bài

Cho tam giác ABC vuông tại A có AB < AC, đường phân giác BD. Vẽ DE vuông góc với BC tại E.

a) Chứng minh trực tâm H của tam giác BAE nằm trên đường thẳng BD.

b) Chứng minh trực tâm của tam giác DAE nằm ngoài tam giác đó.

c) Tìm điều kiện của tam giác ABC để H cách đều các đỉnh của tam giác BAE.

Phương pháp giải - Xem chi tiết

- Chứng minh: BK là đường cao của tam giác BAE và B, K, D thẳng hàng nên trực tâm H của tam giác BAE nằm trên đường thẳng BD.

- Chứng minh: \(\widehat {ADE} > 90^\circ \) nên suy ra trực tâm của tam giác DAE nằm ngoài tam giác đó.

- Tam giác ABE có H là trực tâm, để H cách đều các đỉnh của tam giác BAE thì tam giác BAE là tam giác đều từ đó suy ra điều kiện của tam giác ABC.

Lời giải chi tiết

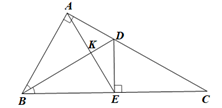
a) Gọi K là giao điểm của BD và AE.

Xét ∆BAD và ∆BED có:

\(\widehat {BAD} = \widehat {BED}\left( { = 90^\circ } \right)\)

BD là cạnh chung,

\(\widehat {ABD} = \widehat {EBD}\) (do BD là tia phân giác của góc ABC)

Do đó ∆BAD = ∆BED (cạnh huyền – góc nhọn).

Suy ra BA = BE (hai cạnh tương ứng).

Xét DABK và DEBK có:

BA = BE (chứng minh trên),

\(\widehat {ABK} = \widehat {EBK}\) (do BD là tia phân giác của góc ABC),

BK là cạnh chung

Do đó DABK =DEBK (c.g.c)

Suy ra \(\widehat {BKA} = \widehat {BKE}\) (hai góc tương ứng).

Mà \(\widehat {BKA} + \widehat {BKE} = 180^\circ \) (hai góc kề bù)

Nên \(\widehat {BKA} = \widehat {BKE} = \frac{{180^\circ }}{2} = 90^\circ \)

Hay BK ⊥ AE.

Do BK là đường cao của tam giác BAE và B, K, D thẳng hàng nên trực tâm H của tam giác BAE nằm trên đường thẳng BD.

Vậy trực tâm H của tam giác BAE nằm trên đường thẳng BD.

b)Ta có \(\widehat {ADE} + \widehat {EDC} = 180^\circ \) (hai góc kề bù)

Mà \(\widehat {EDC} < 90^\circ \) (vì tam giác ECD vuông tại E nên góc EDC là góc nhọn)

Suy ra \(\widehat {ADE} > 90^\circ \)

Do góc ADE là góc tù nên trực tâm của tam giác DAE nằm ngoài tam giác đó.

Vậy trực tâm của tam giác DAE nằm ngoài tam giác đó.

c) Xét tam giác ABE có H là trực tâm, để H cách đều các đỉnh của tam giác BAE thì tam giác BAE là tam giác đều

Do đó \(\widehat {ABE} = 60^\circ \) hay \(\widehat {ABC} = 60^\circ \) Vậy điều kiện để H cách đều các đỉnh của tam giác BAE là tam giác ABC vuông tại A có \(\widehat {ABC} = 60^\circ \).

Bình luận

Chia sẻ

Bình chọn:

4 trên 7 phiếu

Bài tiếp theo

Giải Bài 98 trang 97 sách bài tập toán 7 - Cánh diều
Cho tam giác ABC cân tại A, đường trung tuyến AM. Từ M kẻ ME vuông góc với AB (E ∈ AB), kẻ MF vuông góc với AC (F ∈ AC). Gọi I là giao điểm của AM và EF. Trên tia đối của tia MA lấy điểm D sao cho MD = MA. Chứng minh:
Giải Bài 96 trang 97 sách bài tập toán 7 - Cánh diều
Cho tam giác ABC vuông tại A. Trên tia đối của tia AB lấy điểm D sao cho AB = AD. Vẽ BE vuông góc với CD tại E. Gọi I là giao điểm của AC và BE; K là hình chiếu của I trên BC.
Giải Bài 95 trang 97 sách bài tập toán 7 - Cánh diều
Cho tam giác ABC có trực tâm H đồng thời cũng là điểm cách đều ba đỉnh của tam giác. Tính số đo các góc của tam giác ABC.
Giải Bài 94 trang 97 sách bài tập toán 7 - Cánh diều
Cho tam giác ABC nhọn có các đường cao AD, BE, CF cắt nhau tại H (Hình 61). Tìm trực tâm của các tam giác HAB, HBC, HCA.
Giải Bài 93 trang 97 sách bài tập toán 7 - Cánh diều
Cho tam giác ABC có AB > AC > BC và K là trực tâm. Trong các phát biểu sau, phát biểu nào đúng?
Giải Bài 92 trang 97 sách bài tập toán 7 - Cánh diều
Cho tam giác ABC có AB > AC > BC và H là trực tâm. Trong các phát biểu sau, phát biểu nào đúng, phát biểu nào sai?