Bài 32. Quan hệ giữa đường vuông góc và đường xiên- Kết..

Giải Bài 9.5 trang 50 sách bài tập toán 7 - Kết nối tri thức với cuộc sống

Cho 2 đường thẳng song song c và d. Chứng minh rằng khoảng cách từ mọi điểm thuộc c đến đường thẳng d bằng nhau và bằng khoảng cách từ mọi điểm thuộc đường thẳng d đến đường thẳng c (khoảng cách đó được gọi là khoảng cách giữa hai đường thẳng song song c và d).

Đề bài

Cho 2 đường thẳng song song c và d. Chứng minh rằng khoảng cách từ mọi điểm thuộc c đến đường thẳng d bằng nhau và bằng khoảng cách từ mọi điểm thuộc đường thẳng d đến đường thẳng c (khoảng cách đó được gọi là khoảng cách giữa hai đường thẳng song song c và d).

Phương pháp giải - Xem chi tiết

-Lấy M, M’ thuộc c (M khác M’), kẻ MH, M’H’ vuông góc với d.

-Chứng minh: MH = H’M’ (\(\Delta MHH'\)=\(\Delta H'M'M\))

Lời giải chi tiết

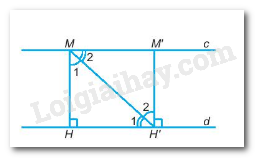
Lấy M, M’ thuộc c (M khác M’), kẻ MH, M’H’ vuông góc với d.

\( \Rightarrow MH\parallel M'H'\)

Xét \(\Delta MHH'\) và \(\Delta H'M'M\)có:

MH’: chung

\(\begin{array}{l}\widehat {{M_1}} = \widehat {H{'_2}}\left( {so\,le\,trong} \right)\\\widehat {{M_2}} = \widehat {H{'_1}}\left( {so\,le\,trong} \right)\\ \Rightarrow \Delta MHH' = \Delta H'M'M\left( {g - c - g} \right)\\ \Rightarrow MH = H'M'\end{array}\)
Vậy khoảng cách từ mọi điểm thuộc c đến đường thẳng d bằng nhau và bằng khoảng cách từ mọi điểm thuộc đường thẳng d đến đường thẳng c.

Bình luận

Chia sẻ

Bình chọn:

4.1 trên 8 phiếu

Bài tiếp theo

Giải Bài 9.6 trang 50 sách bài tập toán 7 - Kết nối tri thức với cuộc sống
Cho 2 điểm phân biệt M, M’ ở cùng phía đối với đường thẳng d (M, M’ không thuộc d). Chứng minh rằng nếu M, M’ có cùng khoảng cách đến đường thẳng d thì MM’ song song với d.
Giải Bài 9.7 trang 50 sách bài tập toán 7 - Kết nối tri thức với cuộc sống
Dùng thước hai lề ta có thể dựng cặp đường thẳng song song với khoảng cách h không đổi. Cho góc xOy. Dùng thước hai lề dựng cặp đường thẳng song song gồm đường thẳng chứa tia Ox và đường thẳng x’ (sao cho x’ cắt Oy) rồi dùng thước hai lề đó, dựng cặp đường thẳng song song gồm đường thẳng chứa tia Oy và đường thẳng y’ (sao cho y’ cắt Ox).Hai đường thẳng x’ và y’ cắt nhau tại P. Chứng minh rằng tia OP là tia phân giác của góc xOy.
Giải Bài 9.8 trang 50 sách bài tập toán 7 - Kết nối tri thức với cuộc sống
Cho tam giác ABC cân tại A. Chứng minh rằng khoảng cách từ B đến đường thẳng AC bằng khoảng cách từ C đến đường thẳng AB.
Giải Bài 9.9 trang 50 sách bài tập toán 7 - Kết nối tri thức với cuộc sống
Cho tam giác ABC cân tại A và một điểm M tuỳ ý thuộc đoạn thẳng BC. Chứng minh rằng tổng khoảng cách từ điểm M đến đường thẳng AB, AC là một số không đổi