 Giải chuyên đề học tập Toán lớp 11 Chân trời sáng tạo
Giải chuyên đề học tập Toán lớp 11 Chân trời sáng tạo
 Bài tập cuối chuyên đề 2 Chuyên đề học tập Toán 11 Chân..
Bài tập cuối chuyên đề 2 Chuyên đề học tập Toán 11 Chân..
Giải bài 9 trang 68 Chuyên đề học tập Toán 11 Chân trời sáng tạo
Có thể vẽ mỗi hình sau đây bằng một nét liền, không nhấc bút khỏi giấy, không vẽ lại đoạn đường nào hai lần không?
Đề bài
Có thể vẽ mỗi hình sau đây bằng một nét liền, không nhấc bút khỏi giấy, không vẽ lại đoạn đường nào hai lần không? Nếu có, hãy chỉ ra một cách vẽ.
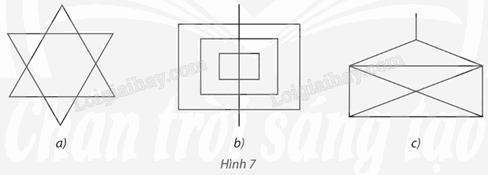
Phương pháp giải - Xem chi tiết
Quan sát hình 7, suy luận để trả lời
Lời giải chi tiết
– Hình 7a:

Gọi tên các đỉnh của đồ thị ở Hình 7a như hình vẽ.
Ta có \(d\left( A \right){\rm{ }} = {\rm{ }}d\left( B \right){\rm{ }} = {\rm{ }}d\left( C \right){\rm{ }} = {\rm{ }}d\left( D \right){\rm{ }} = {\rm{ }}d\left( E \right){\rm{ }} = {\rm{ }}d\left( F \right){\rm{ }} = {\rm{ }}2\) và \(d\left( M \right){\rm{ }} = {\rm{ }}d\left( N \right){\rm{ }} = {\rm{ }}d\left( P \right){\rm{ }} = {\rm{ }}d\left( Q \right){\rm{ }} = {\rm{ }}d\left( R \right){\rm{ }} = {\rm{ }}d\left( S \right){\rm{ }} = {\rm{ }}4.\)
Suy ra đồ thị ở Hình 7a có tất cả các đỉnh đều có bậc chẵn.
Do đó đồ thị ở Hình 7a có chu trình Euler.
Nói cách khác, ta có thể vẽ Hình 7a bằng một nét liền, không nhấc bút khỏi giấy, không vẽ lại đoạn đường nào hai lần.
Chẳng hạn, ta có cách vẽ như sau: NAMSERQCPNBPQDRSFMN.
– Hình 7b:

Gọi tên các đỉnh của đồ thị ở Hình 7b như hình vẽ.
Ta có:
\(\begin{array}{*{20}{l}}{d\left( M \right){\rm{ }} = {\rm{ }}d\left( U \right){\rm{ }} = {\rm{ }}1;}\\{d\left( A \right){\rm{ }} = {\rm{ }}d\left( B \right){\rm{ }} = {\rm{ }}d\left( C \right){\rm{ }} = {\rm{ }}d\left( D \right){\rm{ }} = {\rm{ }}d\left( E \right){\rm{ }} = {\rm{ }}d\left( F \right){\rm{ }} = {\rm{ }}d\left( G \right){\rm{ }} = {\rm{ }}d\left( H \right){\rm{ }} = {\rm{ }}d\left( I \right){\rm{ }} = {\rm{ }}d\left( J \right){\rm{ }} = {\rm{ }}d\left( K \right){\rm{ }} = {\rm{ }}d\left( L \right){\rm{ }} = {\rm{ }}2;}\\{d\left( N \right){\rm{ }} = {\rm{ }}d\left( P \right){\rm{ }} = {\rm{ }}d\left( Q \right){\rm{ }} = {\rm{ }}d\left( R \right){\rm{ }} = {\rm{ }}d\left( S \right){\rm{ }} = {\rm{ }}d\left( T \right){\rm{ }} = {\rm{ }}4.}\end{array}\)
Suy ra đồ thị ở Hình 7b có đúng 2 đỉnh bậc lẻ là M và U.
Do đó đường đi Euler đi từ đỉnh M đến đỉnh U.
Nói cách khác, ta có thể vẽ Hình 7b bằng một nét liền, không nhấc bút khỏi giấy, không vẽ lại đoạn đường nào hai lần.
Chẳng hạn, ta có cách vẽ như sau: MNBCTDANPFGSHEPQJKRLIQRSTU.
– Hình 7c:
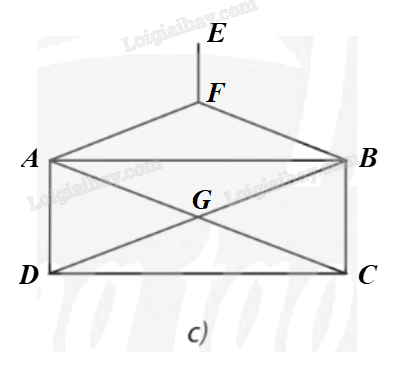
Gọi tên các đỉnh của đồ thị ở Hình 7b như hình vẽ.
Ta có:
\(\begin{array}{*{20}{l}}{d\left( E \right){\rm{ }} = {\rm{ }}1;}\\{d\left( A \right){\rm{ }} = {\rm{ }}d\left( B \right){\rm{ }} = {\rm{ }}d\left( G \right){\rm{ }} = {\rm{ }}4;}\\{d\left( F \right){\rm{ }} = {\rm{ }}d\left( C \right){\rm{ }} = {\rm{ }}d\left( D \right){\rm{ }} = {\rm{ }}3.}\end{array}\)
Suy ra đồ thị ở Hình 7c có 4 đỉnh bậc lẻ.
Do đó đồ thị ở Hình 7c không có đường đi Euler và cũng không có chu trình Euler.
Nói cách khác, ta không thể vẽ Hình 7c bằng một nét liền, không nhấc bút khỏi giấy, không vẽ lại đoạn đường nào hai lần.
- Giải bài 10 trang 69 Chuyên đề học tập Toán 11 Chân trời sáng tạo
- Giải bài 8 trang 68 Chuyên đề học tập Toán 11 Chân trời sáng tạo
- Giải bài 7 trang 67 Chuyên đề học tập Toán 11 Chân trời sáng tạo
- Giải bài 6 trang 67 Chuyên đề học tập Toán 11 Chân trời sáng tạo
- Giải bài 5 trang 67 Chuyên đề học tập Toán 11 Chân trời sáng tạo
>> Xem thêm
Luyện Bài Tập Trắc nghiệm Toán 11 - Chân trời sáng tạo - Xem ngay
Các bài khác cùng chuyên mục
- Giải mục 2 trang 84, 85 Chuyên đề học tập Toán 11 - Chân trời sáng tạo
- Giải bài 3 trang 29 Chuyên đề học tập Toán 11 Chân trời sáng tạo
- Giải bài 11 trang 92 Chuyên đề học tập Toán 11 Chân trời sáng tạo
- Giải bài 12 trang 92 Chuyên đề học tập Toán 11 Chân trời sáng tạo
- Giải bài 10 trang 92 Chuyên đề học tập Toán 11 Chân trời sáng tạo
- Giải mục 2 trang 84, 85 Chuyên đề học tập Toán 11 - Chân trời sáng tạo
- Giải bài 3 trang 29 Chuyên đề học tập Toán 11 Chân trời sáng tạo
- Giải bài 12 trang 92 Chuyên đề học tập Toán 11 Chân trời sáng tạo
- Giải bài 11 trang 92 Chuyên đề học tập Toán 11 Chân trời sáng tạo
- Giải bài 10 trang 92 Chuyên đề học tập Toán 11 Chân trời sáng tạo











