Toán 7, giải toán lớp 7 cánh diều Bài tập cuối chương VI trang 68 SGK Toán 7 cánh diều

Giải bài 7 trang 68 SGK Toán 7 tập 2 - Cánh diều


Tính:

Đề bài

Tính:

a) \(({x^2} + 2x + 3) + (3{x^2} - 5x + 1)\);                         

b) \((4{x^3} - 2{x^2} - 6) - ({x^3} - 7{x^2} + x - 5)\);

c) \( - 3{x^2}(6{x^2} - 8x + 1)\);                                                 

d) \((4{x^2} + 2x + 1)(2x - 1)\);

e) \(({x^6} - 2{x^4} + {x^2}):( - 2{x^2})\);                                  

g) \(({x^5} - {x^4} - 2{x^3}):({x^2} + x)\). 

Phương pháp giải - Xem chi tiết

Muốn cộng (trừ) các đa thức cùng biến với nhau, ta cộng (trừ) các đơn thức có cùng lũy thừa (số mũ) của biến với nhau.

Muốn nhân các đa thức cùng biến với nhau, ta nhân từng đơn thức của đa thức này với đa thức kia rồi cộng chúng lại với nhau.

Muốn chia các đa thức cùng biến với nhau, ta chia đa thức này cho từng đơn thức của đa thức kia rồi cộng chúng lại với nhau.

Lời giải chi tiết

a) \(({x^2} + 2x + 3) + (3{x^2} - 5x + 1) \)

\(= ({x^2} + 3{x^2}) + (2x - 5x) + (3 + 1) \)

\(= 4{x^2} - 3x + 4\) 

b) \((4{x^3} - 2{x^2} - 6) - ({x^3} - 7{x^2} + x - 5) \)

\(= 4{x^3} - 2{x^2} - 6 - {x^3} + 7{x^2} - x + 5\)

\(= (4{x^3} - {x^3}) + ( - 2{x^2} + 7{x^2}) - x + ( - 6 + 5) \)

\(= 3{x^3} + 5{x^2} - x - 1\)

c) \( - 3{x^2}(6{x^2} - 8x + 1) \)

\(=  - 3{x^2}.6{x^2} -  - 3{x^2}.8x +  - 3{x^2}.1\)

\(=  - 18{x^{2 + 2}} + 24{x^{2 + 1}} - 3{x^2} \)

\(=  - 18{x^4} + 24{x^3} - 3{x^2}\)             

d) \((4{x^2} + 2x + 1)(2x - 1) \)

\(= (4{x^2} + 2x + 1).2x - (4{x^2} + 2x + 1).1 \)

\(= 4{x^2}.2x + 2x.2x + 1.2x - 4{x^2} - 2x - 1\)

\(= 8{x^{2 + 1}} + 4{x^{1 + 1}} + 2x - 4{x^2} - 2x - 1 \)

\(= 8{x^3} + 4{x^2} + 2x - 4{x^2} - 2x - 1 \)

\(= 8{x^3} - 1\)

e) \(({x^6} - 2{x^4} + {x^2}):( - 2{x^2}) \)

\(= {x^6}:( - 2{x^2}) - 2{x^4}:( - 2{x^2}) + {x^2}:( - 2{x^2})\)

\(=  - \dfrac{1}{2}{x^{6 - 2}} + {x^{4 - 2}} - \dfrac{1}{2}{x^{2 - 2}} \)

\(=  - \dfrac{1}{2}{x^4} + {x^2} - \dfrac{1}{2}.\)

g) 

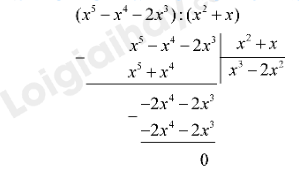
 \(({x^5} - {x^4} - 2{x^3}):({x^2} + x)=x^3-2x^2\)


Bình chọn:
4.2 trên 13 phiếu
Bài tiếp theo

>> Xem thêm

Luyện Bài Tập Trắc nghiệm Toán 7 - Cánh diều - Xem ngay

Báo lỗi - Góp ý

Tham Gia Group Dành Cho 2K12 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí

Các bài khác cùng chuyên mục


App Loigiaihay trên google play store App Loigiaihay trên apple store

Copyright © 2021 loigiaihay.com

DMCA.com Protection Status
App Loigiaihay trên apple store App Loigiaihay trên google play store