Giải bài 7 trang 62 sách bài tập toán 11 - Chân trời sáng tạo tập 2

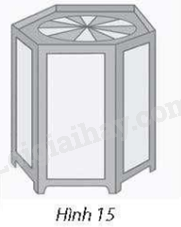
Một hộp đèn treo trần có hình dạng lăng trụ đứng lục giác đều (Hình 15), cạnh đáy bằng 10cm và cạnh bên bằng 50cm. Tính tỉ số giữa diện tích xung quanh và diện tích một mặt đáy của hộp đèn.

Đề bài

Một hộp đèn treo trần có hình dạng lăng trụ đứng lục giác đều (Hình 15), cạnh đáy bằng 10cm và cạnh bên bằng 50cm. Tính tỉ số giữa diện tích xung quanh và diện tích một mặt đáy của hộp đèn.

Phương pháp giải - Xem chi tiết

Sử dụng kiến thức về diện tích xung quanh hình lăng trụ đứng: Diện tích xung quanh hình lăng trụ đứng bằng chu vi đáy nhân chiều cao.

Lời giải chi tiết

Diện tích xung quanh của hình lăng trụ đứng là: \({S_{xq}} = 50.6.10 = 3000\left( {c{m^2}} \right)\)

Hình lăng trụ lục giác đứng lục giác đều có đáy là lục giác đều.

Chia lục giác đều thành 6 tam giác đều như hình vẽ:

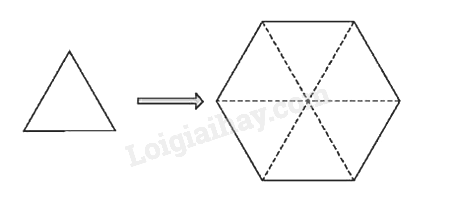
Diện tích một tam giác đều là: \(\frac{{{{10}^2}\sqrt 3 }}{4}\left( {c{m^2}} \right)\)

Diện tích đáy hình lăng trụ đứng lục giác đều là: \({S_{đáy}} = 6.\frac{{{{10}^2}\sqrt 3 }}{4} = 150\sqrt 3 \left( {c{m^2}} \right)\)

Vậy tỉ số giữa diện tích xung quanh và diện tích một mặt đáy của hộp đèn là: \(\frac{{3000}}{{150\sqrt 3 }} = \frac{{20\sqrt 3 }}{3}\)

Bình luận

Chia sẻ

Bình chọn:

4.9 trên 7 phiếu

Bài tiếp theo

Giải bài 6 trang 62 sách bài tập toán 11 - Chân trời sáng tạo tập 2
Người ta cần sơn tất cả các mặt của một khối bê tông hình chóp cụt tứ giác đều, đáy lớn có cạnh bằng 2m, đáy nhỏ có cạnh bằng 1m và cạnh bên bằng 2m (Hình 14). Tính tổng diện tích các bề mặt cần sơn.
Giải bài 5 trang 62 sách bài tập toán 11 - Chân trời sáng tạo tập 2
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, \(SA = a\sqrt 3 \). Hai mặt phẳng (SAB) và (SAD) cùng vuông góc với mặt đáy.
Giải bài 4 trang 61 sách bài tập toán 11 - Chân trời sáng tạo tập 2
Cho hình chóp S.ABCD có đáy ABCD là hình vuông tâm O. Hai mặt phẳng (SAB) và (SAD) cùng vuông góc với mặt phẳng (ABCD).
Giải bài 3 trang 61 sách bài tập toán 11 - Chân trời sáng tạo tập 2
Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại B và \(SA \bot \left( {ABC} \right)\).
Giải bài 2 trang 61 sách bài tập toán 11 - Chân trời sáng tạo tập 2
Cho hình chóp S.ABCD có đáy ABCD là hình vuông tâm O cạnh 2a. Cho biết \(SA = a\) và \(SA \bot \left( {ABCD} \right)\).
Giải bài 1 trang 61 sách bài tập toán 11 - Chân trời sáng tạo tập 2
Cho tứ diện ABCD có tam giác BCD vuông cân tại B và \(AB \bot \left( {BCD} \right)\). Cho biết \(BC = a\sqrt 2 ,AB = \frac{a}{{\sqrt 3 }}\).