Giải bài 3 trang 85 sách bài tập toán 9 - Cánh diều tập 2
Cho tam giác ABC cân tại A có O, I lần lượt là tâm các đường tròn ngoại tiếp và đường tròn nội tiếp tam giác ABC. a) Chứng minh rằng: - Ba điểm A, O, I cùng thuộc một đường thẳng; - Đường thẳng OA vuông góc với BC và đi qua điểm chính giữa D (khác điểm A) của cung BC. b) Cho BC = 24 cm, AC = 20 cm. Tính độ dài bán kính R của đường tròn ngoại tiếp và bán kính r của đường tròn nội tiếp tam giác ABC.
Đề bài
Cho tam giác ABC cân tại A có O, I lần lượt là tâm các đường tròn ngoại tiếp và đường tròn nội tiếp tam giác ABC.
a) Chứng minh rằng:
- Ba điểm A, O, I cùng thuộc một đường thẳng;
- Đường thẳng OA vuông góc với BC và đi qua điểm chính giữa D (khác điểm A) của cung BC.
b) Cho BC = 24 cm, AC = 20 cm. Tính độ dài bán kính R của đường tròn ngoại tiếp và bán kính r của đường tròn nội tiếp tam giác ABC.
Phương pháp giải - Xem chi tiết
Dựa vào tính chất đường kính và dây cung chứng minh \(OH \bot BC\), \(IH \bot BC\) và \(AH \bot BC\).
Chứng minh \(\Delta \)ACH \(\backsim \)\(\Delta \)ADC suy ra R. Dựa vào tỉ số đồng dạng tìm r.
Lời giải chi tiết
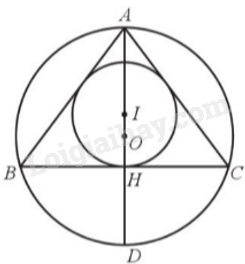
a) Gọi H là chân đường cao hạ từ A.
Tam giác ABC cân tại A, đường cao AH. Suy ra AH là đường trung tuyến của tam giác ABC.
Suy ra BH = HC. Vậy \(OH \bot BC\)(tính chất đường kính và dây cung).
Tương tự, ta có \(IH \bot BC\) mà \(AH \bot BC\)nên A, O, I, H thẳng hàng hay cùng thuộc một đường thẳng.
Ta có A, O, I, H thẳng hàng mà \(OH \bot BC\) nên \(OA \bot BC\). Ta có AD là đường kính của đường tròn (O; OD) nên D cùng nằm trên đường thẳng A, I, O, H suy ra AD là đường trung trực của tam giác ABC. Vậy OA đi qua điểm chính giữa D (khác điểm A) của cung BC.
b) Do BC = 24 cm, AC = 20 cm nên ta có AH = \(\sqrt {A{C^2} - H{C^2}} \) = 16 (cm).
Lại có \(\Delta \)ACH \(\backsim \)\(\Delta \)ADC nên AC2 = AH.AD, suy ra 202 = 16.AD hay AD = 25 cm.
Do đó R = AD : 2 = 12,5 cm.
Do BI là phân giác của góc ABH nên \(\frac{{IH}}{{IA}} = \frac{{BH}}{{BA}} = \frac{{12}}{{20}} = \frac{3}{5}\).
Ta có \(\frac{{IH}}{{IA}} = \frac{3}{5}\) hay \(\frac{{IH}}{{IH + IA}} = \frac{3}{{3 + 5}} = \frac{3}{8}\), tức là \(\frac{r}{{16}} = \frac{3}{8}\). Vì vậy r = 6 cm.
- Giải bài 4 trang 85 sách bài tập toán 9 - Cánh diều tập 2
- Giải bài 5 trang 85 sách bài tập toán 9 - Cánh diều tập 2
- Giải bài 6 trang 85 sách bài tập toán 9 - Cánh diều tập 2
- Giải bài 7 trang 85 sách bài tập toán 9 - Cánh diều tập 2
- Giải bài 8 trang 86 sách bài tập toán 9 - Cánh diều tập 2
>> Xem thêm
Các bài khác cùng chuyên mục













Danh sách bình luận