Bài 1. Vận dụng hệ bất phương trình bậc nhất để giải qu..

Giải bài 3 trang 28 Chuyên đề học tập Toán 12 - Cánh diều

Người ta cần sơn hai loại sản phẩm A, B bằng hai loại sơn: sơn xanh, sơn vàng. Lượng sơn để sơn mỗi loại sản phẩm đó được cho ở Bảng 3 (đơn vị: kg/1 sản phẩm). Người ta dự định sử dụng không quán 12 kg sơn xanh và không quá 8 kg sơn vàng để sơn tất cả các sản phẩm của hai loại đó. Mỗi sản phẩm loại A lãi 10 triệu đồng và mỗi sản phẩm loại B lãi 8 triệu đồng. Tính khối lượng sản phẩm từng loại cần sơn sao cho số tiền lãi thu được là lớn nhất.

Đề bài

Người ta cần sơn hai loại sản phẩm A, B bằng hai loại sơn: sơn xanh, sơn vàng. Lượng sơn để sơn mỗi loại sản phẩm đó được cho ở Bảng 3 (đơn vị: kg/1 sản phẩm).

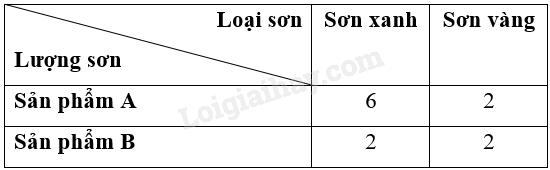
Người ta dự định sử dụng không quán 12 kg sơn xanh và không quá 8 kg sơn vàng để sơn tất cả các sản phẩm của hai loại đó. Mỗi sản phẩm loại A lãi 10 triệu đồng và mỗi sản phẩm loại B lãi 8 triệu đồng. Tính khối lượng sản phẩm từng loại cần sơn sao cho số tiền lãi thu được là lớn nhất.

Phương pháp giải - Xem chi tiết

Đưa bài toán về bài toán quy hoạch tuyến tính sau đó giải bài toán quy hoạch tuyến tính theo các bước sau:

Bước 1: Xác định miền nghiệm \((S)\) của hệ bất phương trình

\(\left\{ \begin{array}{l}{a_1}x + {b_1}y \le {c_1}\\{a_2}x + {b_2}y \le {c_2}\\...\\{a_k}x + {b_k}y \le {c_k}\end{array} \right.\)

Bước 2: Trong tất cả các điểm thuộc \((S)\) tìm điểm \((x,y)\) sao cho biểu thức \(T(x,y)\) có giá trị lớn nhất hoặc nhỏ nhất.

Bước 3: Kết luận.

Lời giải chi tiết

Gọi \(x,y\) lần lượt là số sản phẩm loại A và loại B người đó cần sơn \((x \in N;y \in N)\)

Số tiền lãi người đó thu được là \(T = 10x + 8y\) (triệu đồng)

Vì người đó sử dụng không quá 12 kg sơn xanh nên ta có \(6x + 2y \le 12;\)

Vì người đó sử dụng không quá 8 kg sơn vàng nên ta có \(2x + 2y \le 8;\)

Do người đó muốn số tiền lãi thu được là lớn nhất nên ta có bài toán quy hoạch tuyến tính \(\left\{ \begin{array}{l}\max (T = 10x + 8y)\\6x + 2y \le 12\\2x + 2y \le 8\\x \ge 0\\y \ge 0\end{array} \right.\) (I)

Xét hệ bất phương trình bậc nhất hai ẩn (\(x,y\) là số thực) sau:

\(\left\{ \begin{array}{l}6x + 2y \le 12\\2x + 2y \le 8\\x \ge 0\\y \ge 0\end{array} \right.\) (II)

Ta cần tìm giá trị lớn nhất của biểu thức \(T = 10x + 8y\) khi \((x,y)\) thoả mãn bất phương trình (II)

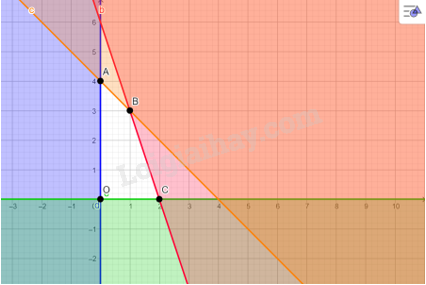
Bước 1. Xác định miền nghiệm của hệ bất phương trình (II)

Miền nghiệm là miền tứ giác OABC với toạ độ các đỉnh \(O(0;0);\) \(A(0;4);\) \(B(1;3)\); \(C(2;0).\)

Bước 2. Tính giá trị biểu thức \(T(x,y) = 10x + 8y\) tại các đỉnh của tứ giác này: \(T(0;0) = 0;\) \(T(0;4) = 32;\) \(T(1;3) = 34;\) \(T(2;0) = 20.\)

Bước 3. Ta đã biết biểu thức \(T = 10x + 8y\) đạt giá trị lớn nhất tại cặp số thực \((x,y)\) là toạ độ một trong các đỉnh của tứ giác OABC. So sánh bốn giá trị thu được của \(T\) ở bước 2, ta được giá trị lớn nhất cần tìm là \(T(1;3) = 34.\)

Bước 4. Vì 1 và 3 đều là các số tự nhiên nên cặp số \((1;3)\) là nghiệm của bài toán (I).

Vậy để số tiền lãi thu được là lớn nhất thì cần sơn 1 sản phẩm loại A và 3 sản phẩm loại B.

Bình luận

Chia sẻ

Bình chọn:

4.9 trên 7 phiếu

Bài tiếp theo

Giải bài 4 trang 28 Chuyên đề học tập Toán 12 - Cánh diều
Một cơ sở sản xuất đồ gỗ dự định sản xuất ba loại sả phẩm là bàn, ghế và tủ. Định mức sử dụng lao động, chi phí sản suất và giá bán mỗi sản phẩm mỗi loại ước tính trong Bảng 4: Biết rằng cơ sở sản xuất đó sử dụng không quá 500 ngày công, số tiền dành cho chi phí sản xuất không quá 40 triệu đồng và số ghế gấp sáu lần số bàn. Tính số sản phẩm mỗi loại cần phải sản xuất sao cho tổng doanh thu đạt được cao nhất.
Giải bài 5 trang 28 Chuyên đề học tập Toán 12 - Cánh diều
Bác Dũng đầu tư không quá 1,2 tỉ đồng vào hai loại cổ phiếu: cổ phiếu A dự kiến chi trả cổ tức bằng tiền với tỉ lệ 5%; cổ phiếu B rủi ro cao hơn dự kiến chi trả cổ tức bằng tiền với tỉ lệ 12%. Giá cổ phiếu A là 30 000 đồng/1 cổ phiếu, giá cổ phiếu B là 40 000 đồng/1 cổ phiếu. Để giảm thiểu rủi ro, bác Dũng quyết định mua số lượng cổ phiếu B không quá 10 000 cổ phiếu. Hỏi bác Dũng nên đầu tư mỗi loại bao nhiêu cổ phiếu để lợi nhuận thu được là lớn nhất.
Giải bài 2 trang 27 Chuyên đề học tập Toán 12 - Cánh diều
Nhu cầu canxi tối thiểu cho một người đang độ tuổi trưởng thành trong một ngày là 1 305 mg. Trong một 1 lạng (100g) đậu nành có 165 mg canxi, 1 lạng thịt có 15 mg canxi. Gia đình chị Thảo có bốn người đang độ tuổi trưởng thành dự định ăn mỗi ngày tối thiểu 3 lạng đậu nàng và 7 lạng thịt, những ăn không quá 4 kg cả đậu nành và thịt. Giá tiền đậu nành là 50 000 đồng/1 kg; giá tiền thịt là 85 000 đồng/1 kg. Hỏi gia đình chị Thảo cần mua bao nhiêu lạng mỗi loại đậu nành và thịt sao cho chi phí để mu
Giải bài 1 trang 27 Chuyên đề học tập Toán 12 - Cánh diều
Để hoàn thành hợp đồng đúng hạn, một nhà mát tổ chức cho công nhân làm việc theo hai ca, ca I từ 7h30 đến 15h30 và ca II từ 6h00 đến 22h00. Mỗi ca có số công nhân làm việc tối thiểu là 40 người và tối đa là 120 người. Số công nhân làm việc ở cả hai ca ít nhất là 100 người. Thu nhập tăng thêm cho mỗi công nhân được tính theo Bảng 2 Tính số lượng công nhân làm việc cho từng ca sao cho số tiền nhà máy trả cho thu nhập tăng thêm là ít nhất.
Giải mục 1 trang 21 Chuyên đề học tập Toán 12 - Cánh diều
Trong bài toán ở phần mở đầu, gọi \(x,y\) lần lượt là số lít nước sinh tố loại thứ nhất và loại thứ hai mà công ty dự định sản xuất. a) Viết các điều kiện ràng buộc đối với \(x,y\) để đáp ứng nhu cầu trên của công ty. b) Viết điều kiện ràng buộc đối với \(x\) và \(y\) sao cho tổng số tiền công ty thu được là nhiều nhất.
Giải Hoạt động mở đầu trang 20 Chuyên đề học tập Toán 12 - Cánh diều
Một công ty kinh doanh đồ uống sản xuất hai loại nước sinh tố theo công thức sau: Trong 1 lít nước sinh tố loại thứ nhất có 0,7 lít nước anh đào; 0,3 lít nước cam và bán với giá là 24 000 đồng/lít. Trong 1 lít nước sinh tố loại thứ hai có 0,4 lít nước anh đào; 0,6 lít nước cam và bán với giá là 18 000 đồng/lít. Công ty có 120 lít nước anh đào và 150 lít nước cam. Hỏi công ty phải sản xuất bao nhiêu lít nước sinh tố mỗi loại sao cho tổng số tiền công ty thu được là nhiều nhất?